Tổng số giờ nắng trong các năm từ 2014 đến 2019 tại hai trạm quan trắc đặt tại Vũng Tàu và Cà Mau được ghi lại ở bảng sau:

Năm	2014	2015	2016	2017	2018	2019
Vũng Tàu	2693,8	2937,8	2690,3	2582,5	2593,9	2814,0
Cà Mau	2195,8	2373,4	2104,6	1947,0	1963,7	2063,9

a) Sử dụng số trung bình, hãy so sánh số giờ nắng mỗi năm của Vũng Tàu và Cà Mau trong 6 năm trên.

b) Sử dụng số trung vị, hãy so sánh số giờ nắng mỗi năm của Vũng Tàu và Cà Mau trong 6 năm trên.

Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:

9   8   15   8   20

b) Giá của một số loại giày (đơn vị nghìn đồng):

350  300  650  300  450  500  300  250

c) Số kênh được chiếu của một số hãng truyền hình cáp:

36  38  33  34  32  30  34  35

Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:

9   8   15   8   20

b) Giá của một số loại giày (đơn vị nghìn đồng):

350  300  650  300  450  500  300  250

c) Số kênh được chiếu của một số hãng truyền hình cáp:

36  38  33  34  32  30  34  35

Hãy chọn số đặc trưng đo xu thế trung tâm của mỗi mẫu số liệu sau. Giải thích và tinh giá trị của số đặc trưng đó.

a) Số mặt trăng đã biết của các hành tinh:

b) Số đường chuyền thành công trong một trận đấu của một số cầu thủ bóng đá:

32 24 20 14 23.

c) Chỉ số IQ của một nhóm học sinh:

d) Các sai số trong một phép đo: 10 15 18 15 14 13 42 15 12 14 42.

Số lượng học sinh giỏi Quốc gia năm học 2018-2019 của 10 trường Trung học phổ thông được cho như sau:

0   0   4   0   0   0   10   0   6   0.

a) Tìm số trung bình, mốt, các tứ phân vị của mẫu số liệu trên.

b) Giải thích tại sao tứ phân vị thứ nhất và trung vị trùng nhau.

Bảng sau đây cho biết số chỗ ngồi của một số sân vận động được sử dụng trong

Giải Bóng đá Vô địch Quốc gia Việt Nam năm 2018 (số liệu gần đúng).

Các giá trị số trung bình, trung vị, mốt bị ảnh hưởng thế nào nếu bỏ đi số liệu chỗ ngồi của Sân vận động Quốc gia Mỹ Đình?

b) \(12;{\rm{ }}32;{\rm{ }}93;{\rm{ }}78;{\rm{ }}24;{\rm{ }}12;{\rm{ }}54;{\rm{ }}66;{\rm{ }}78\).

Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:

a)

b)

An lấy ra ngẫu nhiên 3 quả bóng từ một hộp có chứa nhiều bóng xanh và bóng đỏ. An đếm xem có bao nhiêu bóng đỏ trong 3 bóng lấy ra rồi trả bóng lại hộp. An lặp lại phép thử trên 100 lần và ghi lại kết quả ở bảng sau:

Hãy tìm số trung bình, tứ phân vị và mốt của bảng kết quả trên.

Năm ngoái, thời gian thi của các thí sinh có số trung bình và trung vị đều bằng 7. Bạn hãy so sánh thời gian thi nói chung của các thí sinh trong hai năm.

Bác Dũng và bác Thu ghi lại só điện thoại mà mỗi người gọi mỗi ngày trong 10 ngày được lựa chọn ngẫu nhiên từ tháng 01/2021 ở bảng sau:

a) Hãy tìm số trung bình, tứ phân vị và mốt của số điện thoại mà mỗi bác gọi theo số liệu trên

b) Nếu so sánh theo số trung bình thì ai có nhiều cuộc điện thoại hơn?

c) Nếu so sánh theo số trung vị thì ai có nhiều cuộc điện thoại hơn?

d) Theo bạn, nên dùng số trung bình hay số trung vị để so sánh xem ai có nhiều cuộc gọi điện thoại hơn mỗi ngày?

Kết quả bài kiểm tra giữa kì cả các bạn học sinh lớp 10A, 10B, 10C được thống kê ở các biểu đồ dưới đây.

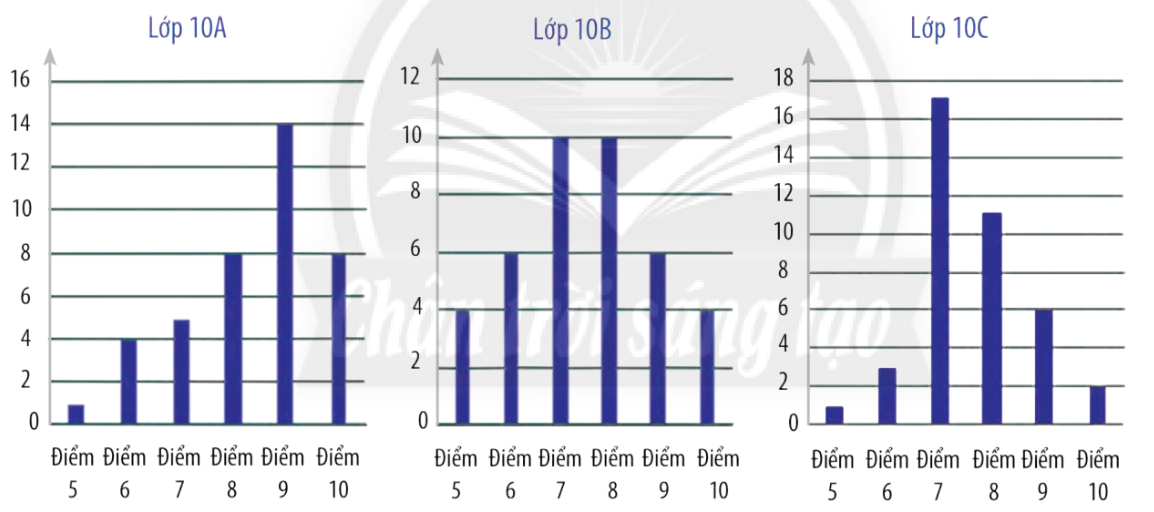
a) Hãy lập thống kê số lượng học sinh theo điểm số ở mỗi lớp.

b) Hãy so sánh điểm số của học sinh các lớp đó theo số trung bình, trung vị và mốt.

Tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:

a) \(15;15;12;14;17;16;16;15;15.\)

b) \(5;7;4;3;5;6;7;8;9;7;2.\)

c) \(7;6;8;7;7;4;5;10;9;9;8;5.\)

d) \(87;87;88;88;70;83;85;86;97;89;92;89;90.\)

a)

b)

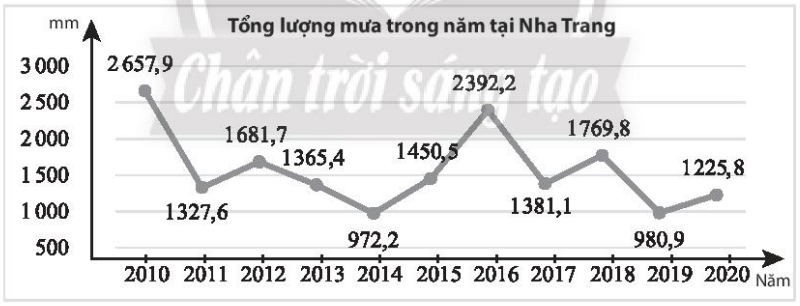
Tổng lượng mưa trong năm tại một trạm quan trắc đặt tại Nha Trang từ 2010 đến 2020 được thể hiện trong biểu đồ sau (đơn vị: mm).

a) Hãy tính lượng mưa trung bình tại trạm quan trắc trên từ 2010 đến 2020.

b) Hãy tìm các tứ phân vị của mẫu số liệu đó.

Số huy chương vàng và bạc trong các giải thể thao quốc tế mà đoàn thể thao Việt Nam đạt được tại các giải đấu ở Châu Á trong các năm từ năm 2010 đến 2019 được thống kê ở bảng sau:

( Nguồn: Tổng cục thống kê)

a) Tìm số trung bình và trung vị huy chương vàng và huy chương bạc mà đoàn thể thao Việt Nam đạt được trong 10 năm trên.

b) Hãy so sánh số huy chương vàng đoàn thể thao Việt Nam đạt được trong gia đoạn 2010 - 2014 với giai đoạn 2015 - 1019.

Bảng sau ghi lại độ tuổi của 2 nhóm vận động viên tham gia một cuộc thi

a) Hãy so sánh độ tuổi hai nhóm vận động viên theo số trung bình và trung vị.

b) Tìm tứ phân vị của độ tuổi vận động viên hai nhóm gộp lại.

Minh và Thủy ghi lại số thư điện tử mà mỗi người nhận được mỗi ngày trong 10 ngày được lựa chọn ngẫu nhiên từ tháng 01/2021 ở bảng sau:

a) Hãy tìm số trung bình, trung vị và mốt của số thư điện tử mà mỗi bạn nhận được theo số liệu trên.

b) Nếu so sánh theo số trung bình thì ai nhận được nhiều thư điện tử hơn?

c) Nếu so sánh theo số trung vị thì ai nhận được nhiều thư điện tử hơn?

d) Nên dùng số trung bình hay số trung vị để so sanh xem ai nhận được nhiều thư điện tử hơn mỗi ngày?

Bạn Út ghi lại khối lượng của một số quả xoài Keo và xoài Thanh Ca ở bảng sau ( đơn vị: gam)

a) Sử dụng số trung bình, hãy so sánh khối lượng của hai loại xoài

b) Sử dụng trung vị, hãy so sánh khối lượng của hai loại xoài.

c) Hãy tính tứ phân vị của hai mẫu số liệu trên.

d) Nếu bạn Út mua 5kg xoài Keo thì sẽ được khoảng bao nhiêu quả?

Nếu bạn Út mua 5kg xoài Thanh Ca thì sẽ được khoảng bao nhiêu quả?

Số đơn vị hành chính cấp quận/huyện/thị xã của các tỉnh/thành phố khu vực Đồng bằng sông Hồng và khu vực Trung du và miền núi phía Bắc vào năm 2019 được cho như sau:

Đồng bằng sông Hồng: 30; 7; 7; 10; 10; 15; 9; 7; 5; 9; 6.

Trung du và miền núi phía Bắc: 10; 12; 7; 6; 8; 8; 7; 10; 9; 12; 9; 7; 11; 10.

( Nguồn: Tổng cục thống kê)

a) Mỗi khu vực nêu trên có bao nhiêu tỉnh/thành phố?

b) Sử dụng số trung bình hãy so sánh số đơn vị hành chính cấp quận/huyện/thị xã của các tỉnh/thành phố ở hai khu vực.

c) Sử dụng số trung vị hãy so sánh số đơn vị hành chính cấp quận/huyện/thị xã của các tỉnh/thành phố ở hai khu vực.

d) Hãy giải thích tại sao lại có sự khác biệt khi so sánh bằng số trung bình và trung vị.

e) Hãy tìm tứ phân vị và mốt của hai khu vực.

Tổng số ca mắc Covid-19 tính đến ngày 26-8-2021 tại Thành phố Hồ Chí Minh và một số tỉnh lân cận được thống kê như sau:

(Theo Bộ Y Tế)

a) Tính số trung bình và trung vị cho dãy số liệu trên.

b) Giải thích tại sao số trung bình và trung vị lại khác nhau nhiều?

Diện tích các tỉnh đồng bằng sông Cửu Long năm 2020 (đơn vị: nghìn \(k{m^2}\)) là:

a) Tính số trung bình, trung vị cho dãy số liệu trên.

b) Giải thích ý nghĩa của mỗi số thu được ở câu a.

Cho mẫu số liệu sau:

156   158   160   162   164

Nếu bổ sung hai giá trị 154, 167 vào mẫu số liệu này thì so với mẫu số liệu ban đầu:

A. Trung vị và số trung bình đều không đổi

B. Trung vị thay đổi, số trung bình không thay đổi

C. Trung vị không thay đổi, số trung bình thay đổi

D. Trung vị và số trung bình đều thay đổi

Thời gian chờ của 10 bệnh nhân (đơn vị: phút) tại một phòng khám được ghi lại như sau:

a) Tính số trung bình, trung vị và mốt của dãy số liệu trên.

b) Nên dùng đại lượng nào để biểu diễn thời gian chờ của bệnh nhân tại phòng khám này?

Chiều cao (đơn vị: xăng-ti-mét) của các bạn tổ I ở lớp 10A lần lượt là:

165 155 171 167 159 175 165 160 158

Đối với mẫu số liệu trên, hãy tìm: 

a) Số trung bình cộng;           

b) Trung vị;                            

c) Mốt;                       

d) Tứ phân vị.

Bảng 3 cho biết tổng diện tích rừng từ năm 2008 đến năm 2019 ở nước ta.

a) Diện tích rừng trung bình của nước ta từ năm 2008 đến năm 2019 là bao nhiêu?

b) Từ năm 2008 đến năm 2019, diện tích rừng của năm có giá trị thấp nhất là bao nhiều triệu héc-ta? Cao nhất là bao nhiêu triệu héc-ta?

c) So với năm 2008, tỉ lệ tổng diện tích rừng của nước ta năm 2019 tăng lên được bao nhiêu phần trăm? Theo em, tỉ lệ tăng đó là cao hay thấp? 

d) Hãy tìm hiểu số liệu về tổng diện tích rừng của tỉnh em đang sống trong một số năm gần đây.

Bảng sau ghi lại số sách mà các bạn học sinh tổ 1 và tổ 2 quyên góp được cho thư viện trường.

a) Sử dụng số trung bình và trung vị, hãy so sánh số sách mà mỗi học sinh tổ 1 và tổ 2 quyên góp được cho thư viện trường.

b) Hãy xác định giá trị ngoại lệ (nếu có) cho mỗi mẫu số liệu. So sánh số sách mà mỗi học sinh tổ 1 và tổ 2 quyên góp được cho thư viện trường sau khi bỏ đi các giá trị ngoại lệ.