Mặt cắt đứng của cột cây số trên quốc lộ có dạng nửa hình tròn ở phía trên và phía dưới có dạng hình chữ nhật (xem hình bên). Biết rằng đường kính của nửa hình tròn cũng là cạnh phía trên của hình chữ nhật và đường chéo của hình chữ nhật có độ dài 66 cm. Tìm kích thước của hình chữ nhật, biết rằng diện tích của phần nửa hình tròn bằng 0,3 lần diện tích của phần hình chữ nhật. Lấy \(\pi = 3,14\) và làm tròn kết quả đến chữ số thập phân thứ hai.
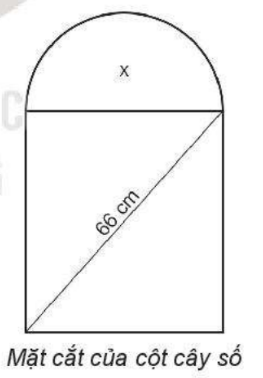
Bước 1: Gọi x là đường kính của nửa hình tròn, biểu diễn diện tích S1 của nửa hình tròn và diện tích S2 của hình chữ nhật theo x
Bước 2: Sử dụng giả thiết S1 = 0,3S2, ta thu được PT bậc hai của x
Bước 3: Giải PT vừa tìm được, suy ra điều kiện của x. Kết luận.
Gọi x (cm) (0 < x < 66) là đường kính của nửa hình tròn
\( \Rightarrow \) Kích thước còn lại của hình chữ nhật là y = \(\sqrt {{{66}^2} - {x^2}} = \sqrt {4356 - {x^2}} \) (cm)
DIện tích của nửa hình tròn là: \({S_1} = \frac{1}{2}\pi .{\left( {\frac{x}{2}} \right)^2} = \frac{{3,14}}{8}{x^2}\) (cm2)
Diện tích hình chữ nhật là: \({S_2} = x\sqrt {4356 - {x^2}} \) (cm2)
Theo giả thiết, \({S_1} = 0,3{S_2} \Leftrightarrow \frac{{3,14}}{8}{x^2} = 0,3.x\sqrt {4356 - {x^2}} \)
\( \Leftrightarrow \frac{{3,14}}{8}{x^2} - 0,3.x\sqrt {4356 - {x^2}} = 0 \Leftrightarrow x\left( {\frac{{3,14}}{8}x - 0,3\sqrt {4356 - {x^2}} } \right)\) = 0
\( \Leftrightarrow \frac{{3,14}}{8}x - 0,3\sqrt {4356 - {x^2}} = 0\) (do x > 0) \( \Leftrightarrow \sqrt {4356 - {x^2}} = \frac{{157}}{{120}}x\) (*)
Bình phương hai vế của (*) ta được: \(4356 - {x^2} = \frac{{24649}}{{14400}}{x^2} \Leftrightarrow {x^2} \approx 1606,35 \Leftrightarrow x \approx 40,08\)
Với x = 40,08 thì y = 52,44
Vậy hai kích thước của hình chữ nhật là 40,08 cm và 52,44 cm

Các bài tập cùng chuyên đề
Giải các phương trình sau:
a) \(\sqrt {2x - 3}=\sqrt {2{x^2} - 3x - 1}\)
b) \(\sqrt {4{x^2} - 6x - 6} = \sqrt {{x^2} - 6} \)
c) \(\sqrt {x + 9} = 2x - 3\)
d) \(\sqrt { - {x^2} + 4x - 2} = 2 - x\)
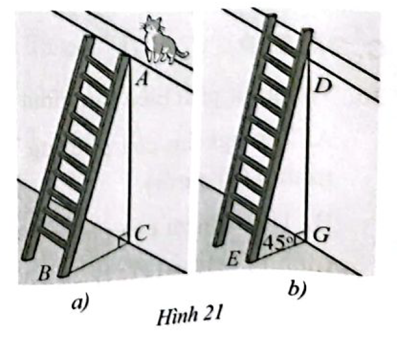
Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó 1 m. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên bức tường (Hình 33a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m thì bác Nam nhận thấy thang tạo với mặt đất một góc \({60^0}\) (Hình 33b). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
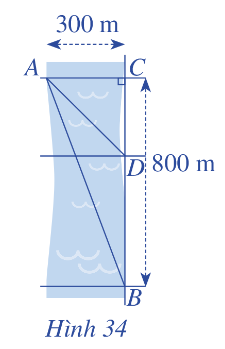
Một người đứng ở điểm A trên một bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m như Hình 34. Vận tốc chèo thuyền là 6 km/h, vận tốc chạy bộ là 10 km/h và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí C đến D, biết tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B (qua D) là 7,2 phút.
Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng cách AB = 4 km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7 km. Người canh hải đăng có thể chèo thuyền từ A đến vị trí M trên bờ biển với vận tốc 3 km/h rồi đi bộ đến C với vận tốc 5 km/h như Hình 35. Tính khoảng cách từ vị trí B đến M, biết thời gian người đó đi từ A đến C là 148 phút.

Giải các phương trình sau:
a) \(\sqrt {x + 2} = x\)
b) \(\sqrt {2{x^2} + 3x - 2} = \sqrt {{x^2} + x + 6} \)
c) \(\sqrt {2{x^2} + 3x - 1} = x + 3\)
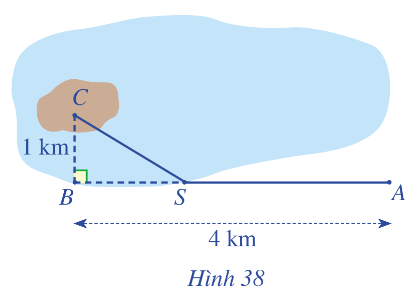
Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.
Hai ô tô xuất phát tại cùng một thời điểm với vận tốc trung bình như nhua là 40km/h từ hai vị trí A và B trên hai con đường vuông góc với nhau để đi về bến O là giao của hai con đường. Vị trí A cách bên 8km, vị trí B cách bên 7 km. Gọi x là thời gian hai xe bắt đầu chạy cho tới khi cách nhau 5km (Hình 31). Bạn Dương xác định được x thỏa mãn phương trình \(\sqrt {{{(8 - 40x)}^2} + {{(7 - 40x)}^2}} = 5\)
Làm thế nào để tìm được giá trị của x?
Giải các phương trình sau:
a) \(\sqrt { - 4x + 4} = \sqrt { - {x^2} + 1} \)
b) \(\sqrt {3{x^2} - 6x + 1} = \sqrt {{x^2} - 3} \)
c) \(\sqrt {2x - 1} = 3x - 4\)
d) \(\sqrt { - 2{x^2} + x + 7} = x - 3\)
Để lao lên một bức tường, bác Dũng dùng một chiếc thang cao hơn bức tường đó 2m. Ban đầu bác Dũng đạt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên của bức tường (Hình 21a). Sau đó bác Dũng dịch chuyển chân thang vào gần chân bức tường thêm 1 m thì bác Dũng thấy thang tạo với mặt đất một góc \({45^ \circ }\). Bức tường cao bao nhiêu mét?
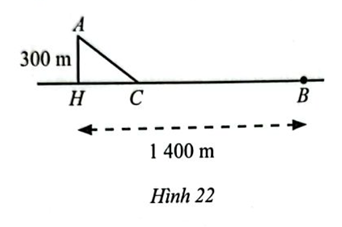
Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6 km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3 km/h. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách AH = 300 m và người đi bộ tại địa điểm cách B một khoảng BH = 1 400 m. Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C (Hình 22).
a) Tính khoảng các CB.
b) Tính thời gian từ khi hai người xuất phát cho đến khi gặp nhau cùng lúc.
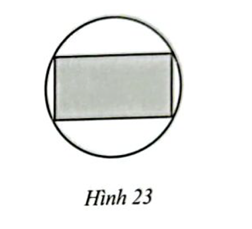
Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50 m (Hình 23). Xác định kích thước vườn hoa hình chữ nhật để tổng quãng đường đi xung quanh vườn hoa đó là 140 m.
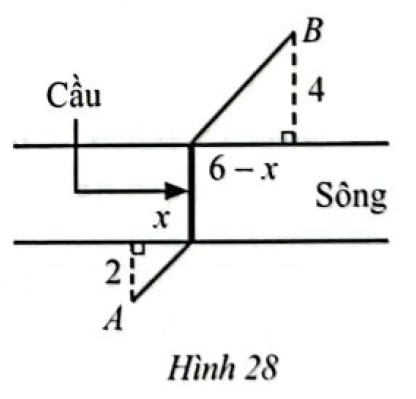
Hai địa điểm A và B cách hai bởi một con sông (coi hai bờ sông song song). Người ta muốn xây một chiếc cầu bắc vuông góc với bờ sông để có thể đi từ A đến B. Với các số liệu (tính theo đơn vị km) cho trên Hình 28, tìm \(x\) (km) để xác định vị trí đặt chân cầu sao cho khoảng cách từ B đến chân cầu phía B gấp đôi khoảng cách từ A đến chân cầu phía A.
Giải các phương trình sau:
a) \(\sqrt {2{x^2} - 14} = x - 1\)
b) \(\sqrt { - {x^2} - 5x + 2} = \sqrt {{x^2} - 2x - 3} .\)
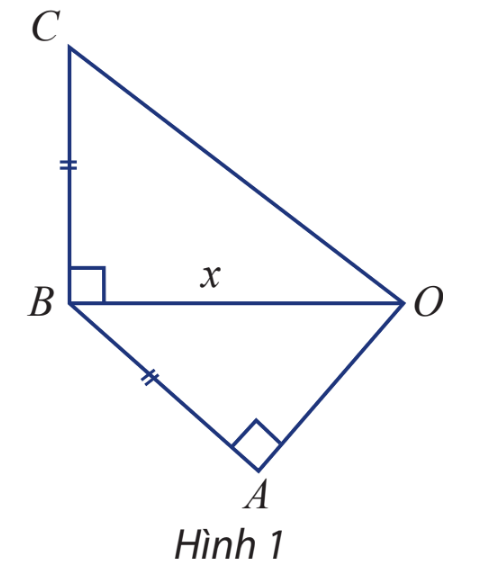
Cho tam giác OAB và OBC lần lượt vuông tại A và B như hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1 cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để:
a) \(OC = 3OA;\)
b) \(OC = \frac{5}{4}OB\)
Giải các phương trình sau:
a) \(\sqrt {11{x^2} - 14x - 12} = \sqrt {3{x^2} + 4x - 7} \)
b) \(\sqrt {{x^2} + x - 42} = \sqrt {2x - 30} \)
c) \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \)
d) \(3\sqrt {{x^2} + x - 1} - \sqrt {7{x^2} + 2x - 5} = 0\)
Cho tam giác ABC vuông tại A có AB ngắn hơn AC là 2 cm.
a) Biểu diễn độ dài cạnh huyền BC theo AB
b) Biết chu vi của tam giác ABC là 24 cm. Tính độ dài ba cạnh của tam giác đó.
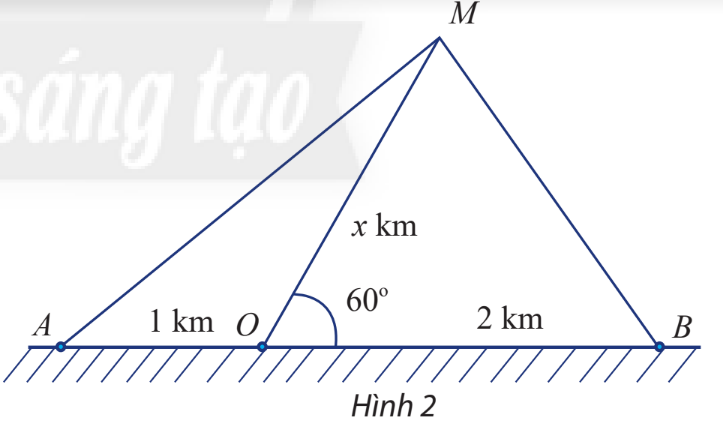
Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc \(60^\circ \). Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng 1km và 2km (Hình 2).
a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.
b) Tìm x để khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A
c) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.
Lưu ý: Làm tròn kết quả đến hàng phần trăm.
Giải các phương trình sau:
a) \(\sqrt {{x^2} - 7x} = \sqrt { - 9{x^2} - 8x + 3} \)
b) \(\sqrt {{x^2} + x + 8} - \sqrt {{x^2} + 4x + 1} = 0\)
c) \(\sqrt {4{x^2} + x - 1} = x + 1\)
d) \(\sqrt {2{x^2} - 10x - 29} = \sqrt {x - 8} \)
Một tam giác vuông có một cạnh góc vuông ngắn hơn cạnh huyền 8 cm. Tính độ dài của cạnh huyền, biết chu vi của tam giác bằng 30 cm.
Khoảng cách từ nhà An ở vị trí N đến cột điện C là 10 m. Từ nhà, An đi x mét theo phương tạo với NC một góc \(60^\circ \) đến vị trí A sau đó đi tiếp 3 m đến vị trí B như hình 1.
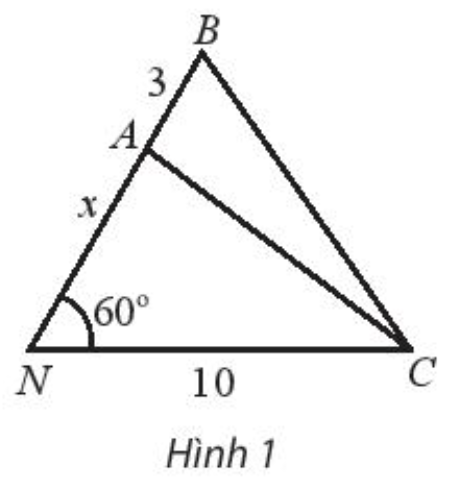
a) Biểu diễn khoảng cách AC và BC theo x.
b) Tìm x để \(AC = \frac{8}{9}BC\).
c) Tìm x để khoảng cách \(BC = 2AN\).
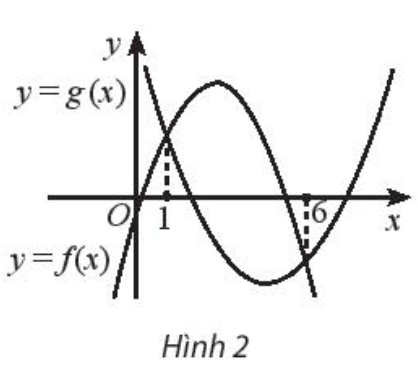
Cho đồ thị của hai hàm số bậc hai \(f\left( x \right) = a{x^2} + bx + c\) và \(g\left( x \right) = d{x^2} + ex + h\) như hình 2. Khẳng định nào đúng với phương trình \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + h} \)?
A. Phương trình có hai nghiệm phân biệt là \(x = 1\) và \(x = 6\)
B. Phương trình có một nghiệm là \(x = 1\)
C. Phương trình có một nghiệm là \(x = 6\)
D. Phương trình vô nghiệm
Giải các phương trình sau:
a) \(\sqrt {3{x^2} + 7x - 1} = \sqrt {6{x^2} + 6x - 11} \)
b) \(\sqrt {{x^2} + 12x + 28} = \sqrt {2{x^2} + 14x + 24} \)
c) \(\sqrt {2{x^2} - 12x - 14} = \sqrt {5{x^2} - 26x - 6} \)
d) \(\sqrt {11{x^2} - 43x + 25} = - 3x + 4\)
e) \(\sqrt { - 5{x^2} - x + 35} = x + 5\)
g) \(\sqrt {11{x^2} - 64x + 97} = 3x - 11\)
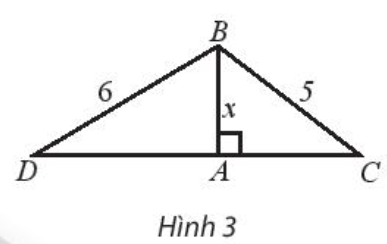
Cho tam giác ABC và ABD cùng vuông tại A như hình 3 có \(AB = x;BC = 5\) và \(BD = 6\).
a) Biểu diễn độ dài cạnh AC và AD theo x.
b) Tìm x để chu vi của tam giác ABC là 12.
c) Tìm x để \(AD = 2AC\).
Giải các phương trình chứa căn thức sau:
a) \(\sqrt {3{x^2} - 4x + 1} = \sqrt {{x^2} - x} \).
b) \(\sqrt {6{x^2} - 11x - 3} = 2x - 1\).
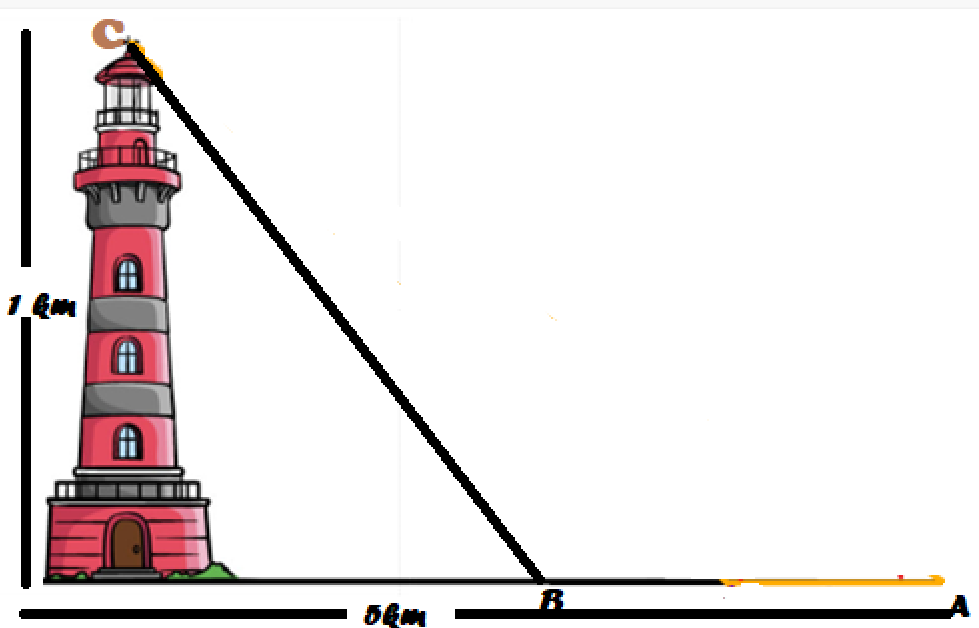
Người ta kéo dây điện từ nguồn điện ở vị trí A đến B rồi kéo lên vị trí C là Ngọn Hải Đăng để chiếu sáng. Biết khoảng cách từ vị trí A đến chân Ngọn Hải Đăng là 5 km, chiều cao Ngọn Hải Đăng là 1 km. Tiền công kéo dây điện bắt từ A đến B là 2 triệu đồng/km và từ B đến C là 3 triệu đồng/km . Hỏi tổng chiều dài dây điện đã kéo từ A đến C là bao nhiêu mét biết tổng chi phí tiền công kéo dây điện là 13 triệu đồng?
a) Tính tổng các nghiệm của phương trình sau: $\sqrt{x^{2} + 2x + 4} = \sqrt{2 - x}$.
b) Tìm m để bất phương trình $x^{2} - \left( {2m - 2} \right)x + m(m + 4) \geq 0$, $\forall x \in {\mathbb{R}}$.








Danh sách bình luận