Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thoi, \(\left( {SAC} \right) \bot \left( {ABCD} \right)\), \(\left( {SBD} \right) \bot \left( {ABCD} \right)\). Chứng minh rằng \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
Để chứng minh 2 mặt phẳng vuông góc, ta cần chứng minh 1 đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia.
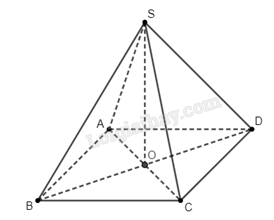
Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Ta dễ dàng chứng minh được \(SO\) là giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\).
Vì \(\left( {SAC} \right) \bot \left( {ABCD} \right)\), \(\left( {SBD} \right) \bot \left( {ABCD} \right)\), \(SO = \left( {SAC} \right) \cap \left( {SBD} \right)\), ta suy ra \(SO \bot \left( {ABCD} \right)\). Điều này dẫn tới \(SO \bot AO\).
Do \(ABCD\) là hình thoi, nên ta có \(AC \bot BD\), hay \(AO \bot BD\).
Như vậy ta có \(SO \bot AO\), \(AO \bot BD\) nên \(AO \bot \left( {SBD} \right)\).
Mà \(AO \subset \left( {SAC} \right)\) nên ta suy ra \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
Bài toán được chứng minh.

Các bài tập cùng chuyên đề
Cho hình chóp S.ABCD, đáy ABCD là một hình chữ nhật có tâm O, SO \( \bot \) (ABCD). Chứng minh rằng hai mặt phẳng (SAC) và (SBD) vuông góc với nhau khi và chỉ khi ABCD là một hình vuông.
Trong HĐ1 của Bài 23, ta đã nhận ra rằng đường thẳng nối các bản lề của cửa phòng vuông góc với sàn nhà. Hãy giải thích vì sao trong quá trình đóng – mở, cánh cửa luôn vuông góc với sàn nhà.
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến a và cùng vuông góc với mặt phẳng (R). Gọi O là một điểm thuộc a và a' là đường thẳng qua O và vuông góc với (R).
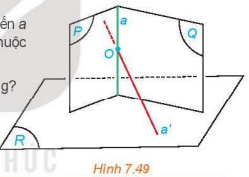
a) Hỏi a' có nằm trong các mặt phẳng (P), (Q) hay không?
b) Tìm mối quan hệ giữa a và a'.
c) Tìm mối quan hệ giữa a và (R).
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Kẻ đường thẳng a thuộc (P) và vuông góc với giao tuyến \(\Delta \) của (P) và (Q). Gọi O là giao điểm của a và \(\Delta \). Trong mặt phẳng (Q), gọi b là đường thẳng vuông góc với \(\Delta \) tại O.
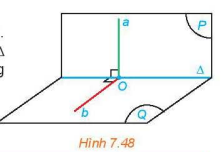
a) Tính góc giữa a và b.
b) Tìm mỗi quan hệ giữa a và (Q).
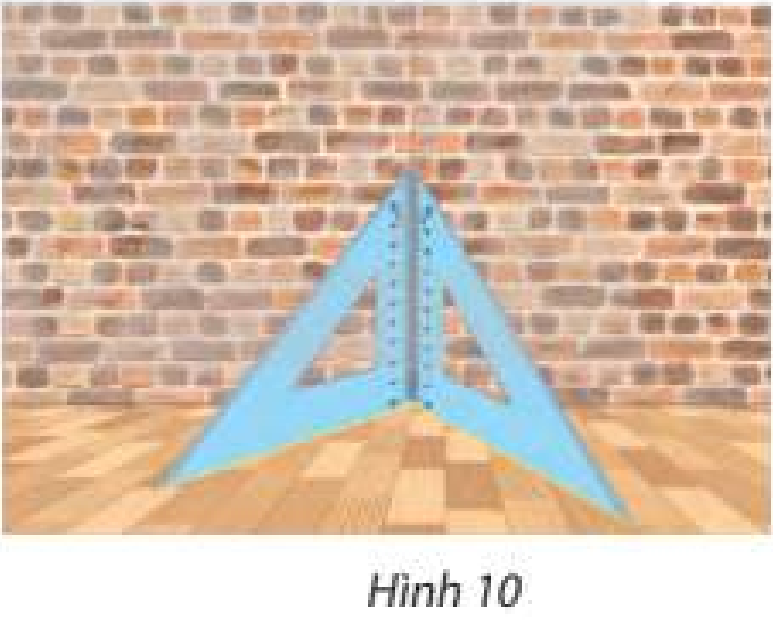
Mô tả cách kiểm tra một bức tường vuông góc với mặt sàn bằng hai cái êke trong Hình 10.
Cho hình chóp \(S.ABCD\) có các cạnh bên bằng nhau và đáy là hình vuông. Chứng minh rằng:
a) \(\left( {SAC} \right) \bot \left( {ABCD} \right)\);
b) \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Gọi \(a\) là giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\). Lấy điểm \(M\) trong \(\left( R \right)\), vẽ hai đường thẳng \(MH\) và \(MK\) lần lượt vuông góc với \(\left( P \right)\) và \(\left( Q \right)\). Hỏi:
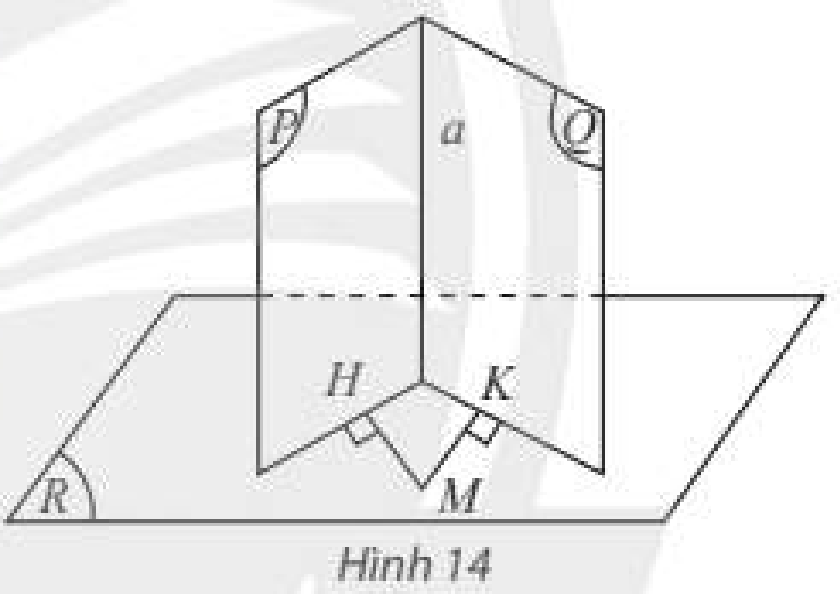
a) Hai đường thẳng \(MH\) và \(MK\) có nằm trong \(\left( R \right)\) không?
b) Đường thẳng \(a\) có vuông góc với \(\left( R \right)\) không?
Cho đường thẳng \(a\) vuông góc với mặt phẳng \(\left( Q \right)\). Mặt phẳng \(\left( P \right)\) chứa \(a\) và cắt \(\left( Q \right)\) theo giao tuyến \(c\). Trong \(\left( Q \right)\) ta vẽ đường thẳng \(b\) vuông góc với \(c\).
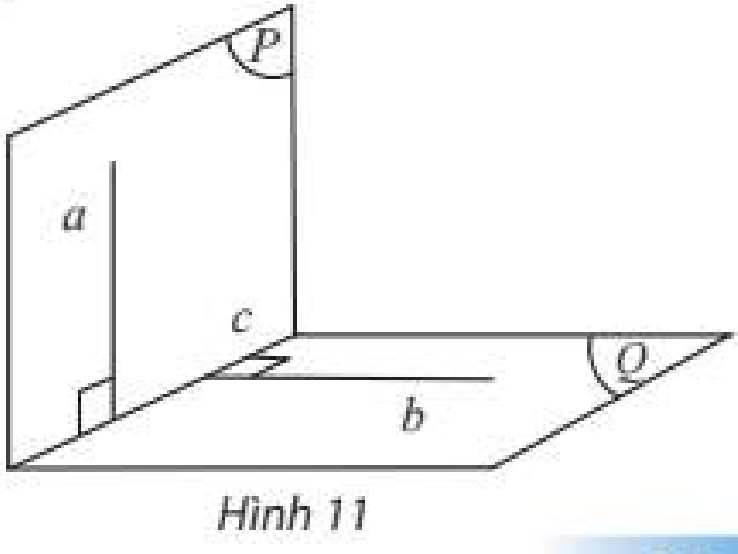
Hỏi:
a) \(\left( P \right)\) có vuông góc với \(\left( Q \right)\) không?
b) Đường thẳng \(b\) vuông góc với \(\left( P \right)\) không?
Cho hình chóp \(S.ABCD\) có các cạnh bên và cạnh đáy đều bằng \(a\). Gọi \(M\) là trung điểm của \({\rm{S}}A\). Mặt phẳng \(\left( {MBD} \right)\) vuông góc với mặt phẳng nào dưới đây?
A. \(\left( {SBC} \right)\).
C. \(\left( {SBD} \right)\).
B. \(\left( {SAC} \right)\).
D. \(\left( {ABCD} \right)\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(SA \bot \left( {ABCD} \right)\). Chứng minh rằng \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
Cho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SC \bot SA\). Chứng minh rằng:
a) \(\left( {SAB} \right) \bot \left( {SBC} \right)\);
b) \(\left( {SBC} \right) \bot \left( {SCA} \right)\);
c) \(\left( {SCA} \right) \bot \left( {SAB} \right)\).
Cho một đường thẳng không vuông góc với mặt phẳng cho trước. Chứng minh rằng tồn tại duy nhất một mặt phẳng chứa đường thẳng đó và vuông góc với mặt phẳng đã cho.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt đáy, tam giác \(SAB\) vuông cân tại \(S\). Gọi \(M\) là trung điểm của \(AB\). Chứng minh rằng:
a) \(SM \bot \left( {ABCD} \right)\);
b) \(AD \bot \left( {SAB} \right)\);
c) \(\left( {SAD} \right) \bot \left( {SBC} \right)\).
Cho tứ diện ABCD có AC = BC, AD = BD. Gọi M là trung điểm của AB. Chứng minh rằng \(\left( {CDM} \right) \bot \left( {ABC} \right)\) và \(\left( {CDM} \right) \bot \left( {ABD} \right)\).
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh bằng a, góc BAD bằng 60 độ. Kẻ OH vuông góc với SC tại H. Biết \(SA \bot \left( {ABCD} \right)\) và \(SA = \frac{{a\sqrt 6 }}{2}\). Chứng minh rằng:
a) \(\left( {SBD} \right) \bot \left( {SAC} \right)\).
b) \(\left( {SBC} \right) \bot \left( {BDH} \right)\).
c) \(\left( {SBC} \right) \bot \left( {SCD} \right)\).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và \(SA \bot \left( {ABC} \right)\).
a) Chứng minh rằng \(\left( {SBC} \right) \bot \left( {SAB} \right)\).
b) Gọi M là trung điểm của AC. Chứng minh rằng \(\left( {SBM} \right) \bot \left( {SAC} \right)\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi H và K lần lượt là hình chiếu của A trên SB và SD. Chứng minh rằng:
a) \(\left( {SBC} \right) \bot \left( {SAB} \right)\);
b) \(\left( {SCD} \right) \bot \left( {SAD} \right)\);
c) \(\left( {SBD} \right) \bot \left( {SAC} \right)\);
d) \(\left( {SAC} \right) \bot \left( {AHK} \right)\).
Cho hình lăng trụ \(ABC.A'B'C'\) có \(AA' \bot \left( {ABC} \right)\), tam giác \(ABC\) cân tại \(A\). Gọi \(M\) là trung điểm của \(BC\). Chứng minh rằng \(\left( {MAA'} \right) \bot \left( {BCC'B'} \right)\).
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\) và \(ABCD\) là hình chữ nhật. Chứng minh rằng:
a) \(\left( {SAB} \right) \bot \left( {SBC} \right)\)
b) \(\left( {SAD} \right) \bot \left( {SCD} \right)\)
Cho hình chóp \(S.ABC\) có \(\widehat {ASB} = \widehat {ASC} = {90^o}\). Gọi \(H\) là trực tâm của tam giác \(ABC\). Chứng minh rằng \(\left( {SAH} \right) \bot \left( {ABC} \right)\).
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông, tam giác \(SAB\) vuông tại \(S\) và nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right)\). Chứng minh rằng:
a) \(\left( {SAD} \right) \bot \left( {SAB} \right)\).
b) \(\left( {SBC} \right) \bot \left( {SAB} \right)\).
c) \(\left( {SAD} \right) \bot \left( {SBC} \right)\).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA⊥(ABCD). Mặt phẳng nào sau đây vuông góc với mặt phẳng (ABCD)?
-
A.
(SAB)
-
B.
(SBC)
-
C.
(SCD)
-
D.
(SBD)
Cho hình chóp tứ giác đều S.ABCD. Khẳng định nào sau đây là đúng?
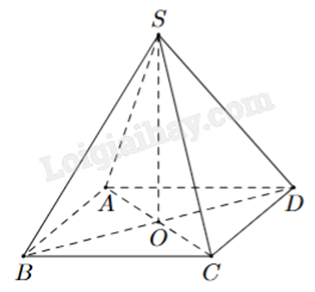
-
A.
\((SAC) \bot (SBD)\)
-
B.
\((SAC) \bot (SCD)\)
-
C.
\((SAC) \bot (SAD)\)
-
D.
\((SAC) \bot (SAB)\)
Cho hình chóp S.ABCD có đáy là hình chữ nhật, $SA\bot(ABCD)$. Chứng minh $(SBC)\bot(SAB)$.







Danh sách bình luận