Cho hình chóp S.ABCD có đáy là hình thoi, O là giao điểm của hai đường chéo, SA = SC, SB = SD.
a) Chứng minh rằng \(SO \bot \left( {ABCD} \right)\).
b) Gọi I, J lần lượt là trung điểm của BA, BC. Chứng minh rằng \(IJ \bot \left( {SBD} \right)\).
c) Chứng minh rằng \(BD \bot \left( {SAC} \right)\).
a, c) Sử dụng kiến thức về định lí đường thẳng vuông góc với mặt phẳng để chứng minh: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
b) Sử dụng kiến thức về liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng: Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
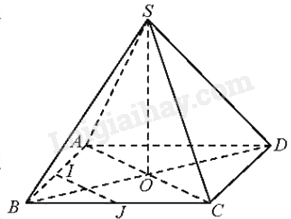
a) Vì ABCD là hình thoi tâm O nên O là trung điểm của AC, O là trung điểm của BD.
Vì \(SA = SC\) nên tam giác SAC cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác SAC. Do đó, \(SO \bot AC\)
Vì \(SB = SD\) nên tam giác SBD cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác SBD. Do đó, \(SO \bot BD\)
Vì \(SO \bot AC\), \(SO \bot BD\), AC và BD cắt nhau và nằm trong (ABCD).
Do đó, \(SO \bot \left( {ABCD} \right)\)
b) Vì \(SO \bot AC,BD \bot AC\) (do ABCD là hình thoi tâm), SO và BD cắt nhau tại O và nằm trong (SBD) nên \(AC \bot \left( {SBD} \right)\) (1)
Vì I, J lần lượt là trung điểm của BA, BC nên IJ là đường trung bình của tam giác BAC. Do đó, IJ//AC (2)
Từ (1) và (2) suy ra: \(IJ \bot \left( {SBD} \right)\).
c) Vì \(SO \bot BD,BD \bot AC\), SO và AC cắt nhau tại O và nằm trong (SAC) nên \(BD \bot \left( {SAC} \right)\).

Các bài tập cùng chuyên đề
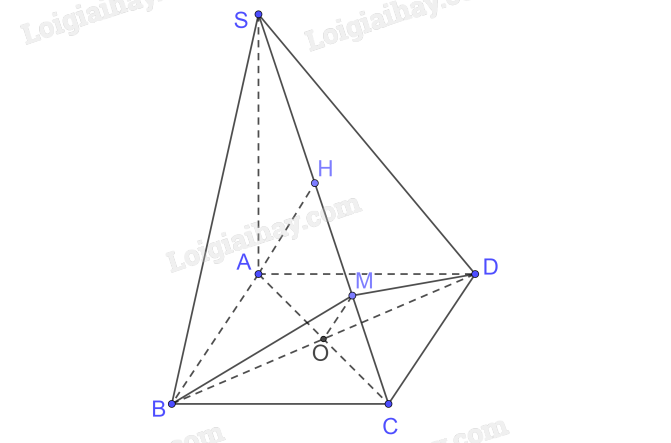
Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA \( \bot \) (ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC). Chứng minh rằng SC \( \bot \) (MBD) và AH // (MBD).
Cho đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng \(\Delta \).
a) Qua một điểm O thuộc (P), kẻ đường thẳng a' song song với a. Nêu vị trí tương đối giữa a' và (P).
b) Nêu vị trí tương đối giữa a và (P).
Cho đường thẳng a song song với mặt phẳng (P) và đường thẳng \(\Delta \) vuông góc với mặt phẳng (P). Tính (\(\Delta \), a).
Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn. Hỏi hai mặt phẳng đó có song song với nhau hay không? Vì sao?
Cho hai mặt phẳng phân biệt (P) và (Q) cùng vuông góc với đường thẳng \(\Delta \). Xét O là một điểm thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q). Gọi (R) là mặt phẳng đi qua O và song song với (Q) (H.7.24).
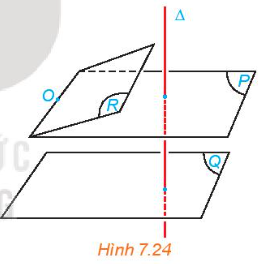
a) Hỏi (R) có vuông góc với Δ hay không? Nêu nhận xét về vị trí tương đối giữa (P) và (R).
b) Nêu vị trí tương đối giữa (P) và (Q).
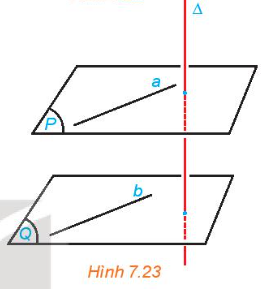
Cho hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng \(\Delta \) vuông góc với (P). Gọi b là một đường thẳng bất kì thuộc (Q). Lấy một đường thẳng a thuộc (P) sao cho a song song với b (H.7.23). So sánh (\(\Delta \), b) và (\(\Delta \), a). Từ đó rút ra mối quan hệ giữa \(\Delta \) và (Q).
Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P). Xét O là một điểm thuộc a nhưng không thuộc b. Gọi c là đường thẳng qua O và song song với b.
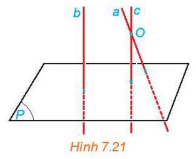
a) Hỏi c có vuông góc với (P) hay không? Nêu nhận xét về vị trí tương đối giữa a và c.
b) Nêu nhận xét về vị trí tương đối giữa hai đường thẳng a và b.
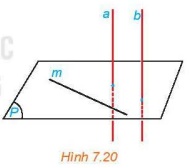
Cho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b. Lấy một đường thẳng m bất kì thuộc mặt phẳng (P). Tính (b, m) và từ đó rút ra mối quan hệ giữa b và (P).
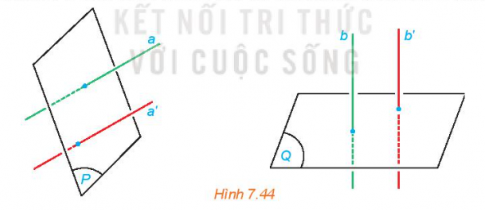
Cho hai mặt phẳng (P) và (Q). Lấy hai đường thẳng a, a' cùng vuông góc với (P), hai đường thẳng b, b' cùng vuông góc với (Q). Tìm mối quan hệ giữa các góc (a,b) và (a', b').
Một kệ sách có bốn trụ chống và các ngăn làm bằng các tấm gỗ (Hình 18). Làm thể nào dùng một êke để kiểm tra xem các tấm gỗ có vuông góc với mỗi trụ chống và song song với nhau hay không? Giải thích cách làm.

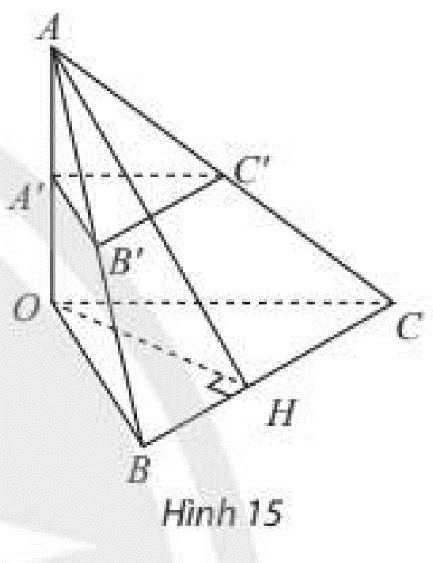
Cho tứ diện \(OABC\) có \(OA\) vuông góc với mặt phẳng \(\left( {OBC} \right)\) và có \(A',B',C'\) lần lượt là trung điểm của \(OA,AB,AC\). Vẽ \(OH\) là đường cao của tam giác \(OBC\). Chứng minh rằng:
a) \(OA \bot \left( {A'B'C'} \right)\);
b) \(B'C' \bot \left( {OAH} \right)\).
Nêu nhận xét về vị trí tương đối của:
a) Hai thân cây cùng mọc vuông góc với mặt đất.
b) Mặt bàn và mặt đất cùng vuông góc với chân bàn.
c) Thanh xà ngang nằm trên trần nhà và mặt sàn nhà cùng vuông góc với cột nhà.

Cho hình chóp S.ABC có SA ⊥ (ABC). Mặt phẳng (P) khác với mặt phẳng (ABC), vuông góc với đường thẳng SA và lần lượt cắt các đường thẳng SB, SC tại hai điểm phân biệt B', C'. Chứng minh rằng B'C' // BC.
Cho đường thẳng d và mặt phẳng (P) cắt nhau tại điểm O. Lấy các điểm A, B thuộc d khác O; các điểm A', B' thuộc (P) thỏa mãn \(AA' \bot (P),\,BB' \bot (P)\). Chứng minh rằng: \(\frac{{AA'}}{{BB'}} = \frac{{OA}}{{OB}}\).
Trong Hình 21 , hai mặt sàn của nhà cao tầng và cột trụ bê tông gợi nên hình ảnh hai mặt phẳng (P), (Q) phân biệt và đường thẳng a.

Quan sát Hình 21 và cho biết:
a) Nếu hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng a vuông góc với mặt phẳng (P) thì đường thẳng a có vuông góc với mặt phẳng (Q) hay không?
b) Nếu hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng a thì chúng có song song với nhau hay không?
Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P). Quan sát Hình 19 và cho biết:
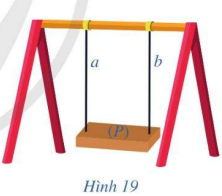
a) Nếu hai đường thẳng a và b song song với nhau và mặt phẳng (P) vuông góc với đường thẳng a thì mặt phẳng (P) có vuông góc với đường thẳng b hay không?
b) Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng (P) thì chúng có song song với nhau hay không?
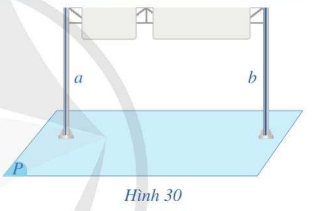
Quan sát Hình 30 (hai cột của biển báo, mặt đường), cho biết hình đó gợi nên tính chất nào về quan hệ vuông góc giữa đường thẳng và mặt phẳng.
Cho đường thẳng a vuông góc với mặt phẳng (P), đường thẳng b vuông góc với đường thẳng a. Phát biểu nào sau đây là đúng?
A. Đường thẳng \(b\) cắt mặt phẳng \(\left( P \right)\)
B. Đường thẳng \(b\) song song mặt phẳng \(\left( P \right)\)
C. Đường thẳng \(b\) nằm trên mặt phẳng \(\left( P \right)\)
D. Đường thẳng \(b\) nằm trên mặt phẳng \(\left( P \right)\) hoặc song song mặt phẳng \(\left( P \right)\)
Cho tứ diện ABCD có \(DA \bot \left( {ABC} \right)\), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ \(AH \bot MD\) tại H.
a) Chứng minh rằng \(AH \bot \left( {BCD} \right)\).
b) Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Chứng minh rằng \(GK \bot \left( {ABC} \right)\).
Cho hai mặt phẳng \(\left( P \right)\), \(\left( Q \right)\) vuông góc và cắt nhau theo giao tuyến \(d\), đường thẳng \(a\) song song với \(\left( P \right)\). Phát biểu nào sau đây là đúng?
A. Nếu \(a \bot d\) thì \(a \bot \left( Q \right)\).
B. Nếu \(a \bot d\) thì \(a\parallel \left( Q \right)\).
C. Nếu \(a \bot d\) thì \(a\parallel b\) với mọi \(b \subset \left( Q \right)\).
D. Nếu \(a \bot d\) thì \(a\parallel c\) với mọi \(c\parallel \left( Q \right)\).
Trong không gian, cho 3 đường thẳng a, b, c phân biệt và mặt phẳng (P). Mệnh đề nào sau đây
đúng?
-
A.
Nếu \(a \bot c\) và \(b \bot c\) thì a // b
-
B.
Nếu \(a \bot b\) và \(b \bot c\) thì \(a \bot c\)
-
C.
Nếu \(a \bot b\) thì a và b cắt nhau hoặc chéo nhau
-
D.
Nếu \(a \bot c\) và \((P) \bot c\) thì a // (P)
Trong không gian cho hai đường thẳng phân biệt a, b và mặt phẳng (P), trong đó \(a \bot (P)\). Mệnh đề nào sau đây sai?
-
A.
Nếu b // a thì \(b \bot (P)\)
-
B.
Nếu \(b \bot a\) thì b // (P)
-
C.
Nếu b // (P) thì \(b \bot a\)
-
D.
Nếu \(b \bot (P)\) thì b // a







Danh sách bình luận