Người ta cắt bỏ bốn hình vuông cùng kích thước ở bốn góc của một tấm tôn hình vuông có cạnh 1 m để gò lại thành một chiếc thùng có dạng hình hộp chữ nhật không nắp. Hỏi cạnh của các hình vuông cần bỏ đi có độ dài bằng bao nhiêu để thùng hình hộp nhận được có thể tích lớn nhất?
Áp dụng công thức tính thể tích khối hộp chữ nhật: \({\rm{V}} = a.b.c\).
Trong đó: \(a,b,c\) là độ dài 3 cạnh hình hộp chữ nhật có chung 1 đỉnh
Bước 1: Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với \(0 < x < \frac{1}{2}\) ).
Tính thể tích hình hộp chữ nhật nhận được.
Bước 2: Tìm giá trị lớn nhất của thể tích hình hộp chữ nhật nhận được.
Từ đó tìm \(x\).
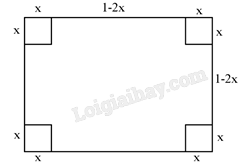
Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với \(0 < x < \frac{1}{2}\) ).
Thể tích hình hộp chữ nhật nhận được là:
\(V = {(1 - 2x)^2} \cdot x = \frac{1}{4} \cdot \left( {1 - 2x} \right) \cdot \left( {1 - 2x} \right) \cdot 4x \le \frac{1}{4} \cdot {\left( {\frac{{1 - 2x + 1 - 2x + 4x}}{3}} \right)^3} = \frac{2}{{27}}\)
Dấu "=" xảy ra khi \(1 - 2x = 4x \Leftrightarrow x = \frac{1}{6}\).
Vậy để thể tích chiếc thùng là lớn nhất thì các cạnh của hình vuông được cắt bỏ đi là \(\frac{1}{6}{\rm{\;m}}\).
Các bài tập cùng chuyên đề
Khi mua máy điều hoà, bác An được hướng dẫn rằng mỗi mét khối của phòng cần công suất điều hoà khoảng 200 BTU. Căn phòng bác An cần lắp máy có dạng hình hộp chữ nhật, rộng 4 m, dài 5 m và cao 3 m. Hỏi bác An cần mua loại điều hoà có công suất bao nhiêu BTU?
Cho một khối hộp chữ nhật với các kích thước là \(a,b,c\) đều là số nguyên dương. Về các mặt phẳng song song với các mặt của hình hộp và chia nó thành các khối lập phương có cạnh bằng 1 (Hình 11). Tìm số hình lập phương đơn vị có trong hình hộp.
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = 2a\) và đáy \(ABCD\) là hình thoi có \(AB = a\) và \(AC = a\sqrt 3 \).
a) Tính khoảng cách giữa hai đường thẳng \(B{\rm{D}}\) và \(AA'\).
b) Tính thể tích của khối hộp.
Cho hình hộp \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = a\), đáy \(ABCD\) là hình thoi có \(AB = BD = a\). Hình chiếu vuông góc của \(A'\) lên mặt đáy trùng với điểm \(O\) là giao điểm hai đường chéo của đáy. Tính thể tích của khối hộp.
Một chiếc bánh chưng có dạng khối hộp chữ nhật với kích thước ba cạnh là 15 cm, 15 cm và 6 cm. Tính thể tích của chiếc bánh chưng đó.
Gọi V là thể tích của hình lập phương ABCD.A’B’C’D’. \({V_1}\) là thể tích của tứ diện A’ABD. Hệ thức nào sau đây là đúng?
A. \(V = 6{V_1}\)
B. \(V = 4{V_1}\)
C. \(V = 3{V_1}\)
D. \(V = 2{V_1}\)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và \(SA = a\sqrt 3 \). Thể tích khối chóp S.ABC bằng
