Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, biết \(SO \bot \left( {ABCD} \right)\), \(AC = 2a\sqrt 3 ,BD = 2a\) và khoảng cách từ điểm A đến mặt phẳng (SBC) bằng \(\frac{{a\sqrt 3 }}{2}\). Tính theo a thể tích khối chóp S.ABCD.
Áp dụng công thức tính thể tích khối chóp: \({\rm{S}} = \frac{1}{3}{\rm{Bh}}\).
Trong đó: \({\rm{B}}\) là diện tích đa giác đáy, h là đường cao của hình chóp.
Bước 1: Tính chiều cao \(SO\) của hình chóp.
Phân tích: \(d\left( {A,\left( {SBC} \right)} \right) = 2 \cdot d\left( {O,\left( {SBC} \right)} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right)\)
Dựng hình
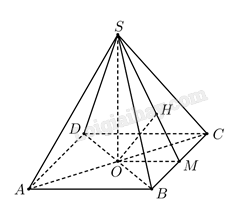
Khoảng cách từ \(d\left( {O,\left( {SBC} \right)} \right) = OH\).
Xét tam giác \(SOM\) vuông tại \(O\), đường cao \(OH\) nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{O{S^2}}}\), suy ra \(SO\).
Bước 2: Tính diện tích đáy \(ABCD\).
Bước 3: Tính thể tích khối chóp \(S.ABCD\): \({V_{S \cdot ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO\).
Kẻ \(OM\) vuông góc với \(BC\) tại \(M,OH\) vuông góc với \(SM\) tại \(H\), ta chứng minh được \(OH \bot \left( {SBC} \right)\). Vì \(O\) là trung điểm của \(AC\) nên\(d\left( {A,\left( {SBC} \right)} \right) = 2 \cdot d\left( {O,\left( {SBC} \right)} \right) = 2 \cdot OH = \frac{{a\sqrt 3 }}{2}\),
suy ra \({\rm{OH}} = \frac{{{\rm{a}}\sqrt 3 }}{4}\).
Tam giác \(OBC\) vuông tại \(O\), có \(OB = a,OC = a\sqrt 3 \)
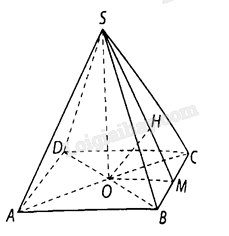
và đường cao \(OM\) nên \(OM = \frac{{OB \cdot OC}}{{BC}} = \frac{{a\sqrt 3 }}{2}\).
Tam giác \(SOM\) vuông tại \(O\), đường cao \(OH\) nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{O{S^2}}}\), suy ra \(SO = \frac{a}{2}\).
Vậy \({V_{S \cdot ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{1}{3} \cdot \frac{1}{2} \cdot 2a\sqrt 3 \cdot 2a \cdot \frac{a}{2} = \frac{{{a^3}\sqrt 3 }}{3}\).
Các bài tập cùng chuyên đề
Cho khối chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích của khối chóp.
Cho khối chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b. Tính thể tích của khối chóp đó. Từ đó suy ra thể tích của khối tứ diện đều có cạnh bằng a.
Cho khối chóp đều S.ABCD, đáy có cạnh 6 cm. Tính thể tích của khối chóp đó trong các trường hợp sau.
a) Cạnh bên tạo với mặt đáy một góc bằng \({60^0}.\)
b) Mặt bên tạo với mặt đáy một góc bằng \({45^0}.\)
Thể tích của khối chóp có diện tích đáy bằng \({\bf{S}}\), chiều cao bằng \(h\) là:
A. \(V = {\bf{S}}.h\).
B. \(V = \frac{1}{2}{\bf{S}}.h\).
C. \(V = \frac{1}{3}{\bf{S}}.h\).
D. \(V = \frac{2}{3}{\bf{S}}.h\).
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, \(AB//CD\) và \(AB = BC = DA = a\), \(CD = 2a\). Biết hai mặt phẳng \((SAC)\) và \((SBD)\) cùng vuông góc với mặt phẳng đáy \((ABCD)\) và \(SA = a\sqrt 2 \). Tính theo \(a\) khoảng cách từ \(S\) đến mặt phẳng \((ABCD)\) và thể tích của khối chóp S.ABCD.
Cho tứ diện đều ABCD có cạnh bằng \(a\). Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD. Thể tích khối chóp \(B\).CMND bằng
A. \(\frac{{{a^3}\sqrt 2 }}{{12}}\)
B. \(\frac{{{a^3}\sqrt 2 }}{{16}}\).
C. \(\frac{{{a^3}\sqrt 2 }}{{24}}\).
D. \(\frac{{{a^3}\sqrt 2 }}{8}\).
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a,AA' = a\sqrt 2 \). Gọi M, N lần lượt là trung điểm của cạnh \(BB'\) và \(CC'\). Mặt phẳng \(\left( {A'MN} \right)\) cắt đường thẳng AB, AC tương ứng tại \(H\) và \(K\).
a) Chứng minh rằng \(MN//HK\).
b) Tính theo a thể tích khối chóp A'.AHK.
Cho khối tứ diện đều \(ABCD\) cạnh \(a\). Chứng minh rằng thể tích của khối tứ diện đó bằng \(\frac{{{a^3}\sqrt 2 }}{{12}}\).
Một loại đèn đá muối có dạng khối chóp tứ giác đều (Hình 97). Tính theo \(a\) thể tích của đèn đá muối đó, giả sử các cạnh đáy và các cạnh bên đều bằng \(a\).
Cho khối chóp có diện tích đáy là \({a^2}\) và chiều cao là \(3a\). Thể tích của khối chóp bằng:
A. \({a^3}\).
B. \(3{a^3}\).
C. \(\frac{{{a^3}}}{3}\).
D. \(9{a^3}\).
Cho tứ diện \(OABC\) thoả mãn \(OA = a,OB = b,OC = c,\) \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {90^ \circ }\). Thể tích của khối tứ diện \(OABC\) bằng:
A. \(abc\).
B. \(\frac{{abc}}{2}\).
C. \(\frac{{abc}}{3}\).
D. \(\frac{{abc}}{6}\).
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\), \(AB = a\), \(AC = a\sqrt 2 \) và \(\widehat {SBA} = 60^\circ \), \(\widehat {BAC} = 45^\circ \). Tính theo a thể tích khối chóp S.ABC.
Cho khối chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a, góc giữa mặt phẳng ({SCD) và mặt phẳng (ABCD) bằng \(60^\circ \). Tính theo a thể tích khối chóp S.ABCD.
Cho tứ diện OABC có OA = OB = OC = a và \(\widehat {AOB} = 90^\circ ;\) \(\widehat {BOC} = 60^\circ \); \(\widehat {COA} = 120^\circ \). Tính theo a thể tích khối tứ diện OABC.
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right),SA = a\) và đáy ABC là tam giác vuông tại A, AB = a, AC = \(a\sqrt 3 \). Kẻ AM vuông góc với SB tại M, AN vuông góc với SC tại N. Tính theo a thể tích khối chóp S.AMN.
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\) và \(\widehat {BAC} = {60^ \circ }\), biết diện tích các tam giác \(ABC,SAB\) và \(SAC\) lần lượt là \(3\sqrt 3 ;9;12\). Tính thể tích khối chóp \(S.ABC\).
Cho hình lập phương ABCD.A’B’C’D’ thể tích khối tứ diện ABC’D’ bằng
A. \(\frac{{{a^3}}}{3}\).
B. \(\frac{{{a^3}}}{2}\).
C. \(\frac{{{a^3}}}{6}\).
D. \(\frac{{2{a^3}}}{3}\).
Cho hình chóp tam giác S.ABC có tam giác ABC vuông cân tại B, \(AC = a\sqrt 2 \), mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng \({60^0}\). Tính theo a thể tích V của khối chóp S.ABC.
Cho hình chóp S. ABCD có SA vuông góc với mặt phẳng (ABCD) và \(SA = a\sqrt 3 \), đáy ABCD là hình thang vuông tại A và B có \(AB = a,AD = 3a,BC = a\). Tính thể tích khối chóp S.BCD theo a.
Một hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước 2cm, 3cm và 6cm. Tính thể tích của khối tứ diện ACB’D’.
Cho khối chóp S.ABCD có đáy là hình chữ nhật \(AB = a,AD = a\sqrt 3 \), SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc \({30^0}\). Tính thể tích V của khối chóp đã cho.
A. \(V = \frac{{2{a^3}\sqrt 6 }}{3}\)
B. \(V = \frac{{{a^3}\sqrt 6 }}{3}\)
C. \(V = 2\sqrt 6 {a^3}\)
D. \(V = \frac{{4{a^3}}}{3}\)
Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(AB = 2a,AD = a\). Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng \({45^0}\). Khi đó thể tích khối chóp S.ABCD là
A. \(\frac{{\sqrt 3 }}{3}{a^3}\)
B. \(\frac{1}{3}{a^3}\)
C. \(2{a^3}\)
D. \(\frac{2}{3}{a^3}\)
Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), tam giác ABC có độ dài 3 cạnh là \(AB = 5a,BC = 8a,AC = 7a\), góc giữa SB và (ABC) là \({45^0}\). Tính thể tích khối chóp S.ABC.
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B’AC) tạo với đáy một góc \({30^0}\), khoảng cách từ B đến mặt phẳng (D’AC) bằng \(\frac{a}{2}\). Tính thể tích khối tứ diện ACB’D’.
Cho hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có \(AB = AD = a,AA' = a\sqrt 2 \). Thể tích khối tứ diện \(ACB'D'\) bằng
A. \(\frac{{{a^3}\sqrt 2 }}{3}\).
B. \(\frac{{{a^3}\sqrt 2 }}{6}\).
C. \(\frac{{{a^3}\sqrt 6 }}{3}\).
D. \(\frac{{{a^3}\sqrt 6 }}{6}\).
Thể tích khối chóp có diện tích đáy bằng B và chiều cao bằng h là
