Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \((O)\) và \(AB < AC\). Lấy điểm \(M\) thuộc cung \(BC\) không chứa điểm \(A\). Vẽ \(MH,MK\) lần lượt vuông góc với \(BC,AC\). Qua \(A\) kẻ đường thẳng song song với \(BC\) cắt \((O)\) tại \(N\). Gọi\(E\) là giao điểm của \(BC\) và \(MN\). Giả sử \(AC = 8,15\,cm\,;\,MK = 4\,cm\,;\,MH = 1,46\,cm\). Khi đó \(E\) cách \(B\) một khoảng có độ dài là bao nhiêu cm? ( Kết quả làm tròn đến số thập phân thứ hai )
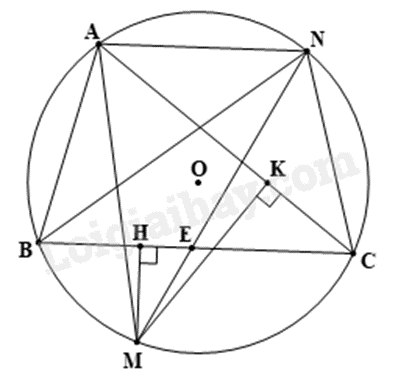
Đáp án:
Đáp án:
Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Chứng minh $\Delta BME\backsim \Delta AMC\left( g.g \right)$. Khi đó tỉ số các đường cao của hai tam giác bằng tỉ số đồng dạng của hai tam giác đó.
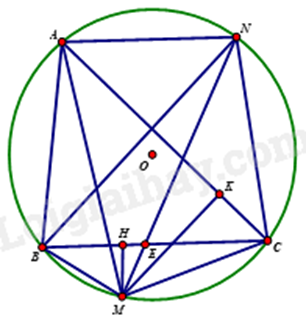
Vì \(AN\,{\rm{//}}\,BC\) nên \(\widehat {ANB} = \widehat {NBC}\) (hai góc so le trong)
Mà \(\widehat {ANB}\) chắn cung AB, \(\widehat {NBC}\) chắn cung NC nên (Các góc nội tiếp bằng nhau chắn các cung bằng nhau)
Suy ra \(\widehat {AMB} = \widehat {NMC}\) (hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau)
Ta có: \(\widehat {AMC} = \widehat {NMC} + \widehat {AMN}\); \(\widehat {BME} = \widehat {AMB} + \widehat {AMN}\)
Suy ra: \(\widehat {AMC} = \widehat {BME}\)
Xét \(\Delta BME\) và \(\Delta AMC\)
\(\widehat {AMC} = \widehat {BME}\)
\(\widehat {MBC} = \widehat {MAC}\) (hai góc nội tiếp cùng chắn cung \(MC\))
Suy ra $\Delta BME\backsim \Delta AMC\,(g-g)$
Vì \(MH,MK\) là hai đường cao tương ứng của tam giác \(\Delta BME;\Delta AMC\) nên: \(\begin{array}{l}\frac{{MH}}{{MK}} = \frac{{BE}}{{AC}}\\\frac{{1,46}}{4} = \frac{{BE}}{{8,15}}\\BE = \frac{{8,15.1,46}}{4} \approx 2,97\,\left( {cm} \right)\end{array}\)
Đáp án: 2,97

Các bài tập cùng chuyên đề
Cho hình vẽ. Khi đó đáp án đúng là
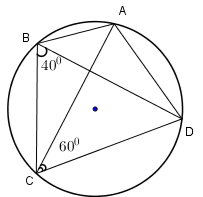
-
A.
\(\widehat {ADC} = {70^0}\)
-
B.
\(\widehat {ADC} = {80^0}\)
-
C.
\(\widehat {ADC} = {75^0}\)
-
D.
\(\widehat {ADC} = {60^0}\)
Cho tứ giác ABCD có \(\widehat A = \widehat C = {90^o}\) (H.9.28). Hãy giải thích vì sao bốn đỉnh của tứ giác ABCD cùng nằm trên một đường tròn có tâm là trung điểm O của đoạn thẳng BD.
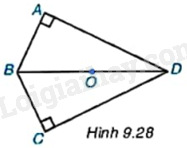
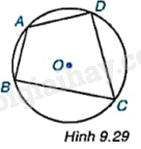
Trên đường tròn (O), lấy các điểm A, B, C, D sao cho tứ giác ABCD là tứ giác lồi (H.9.29). Các đường trung trực của các cạnh AB, BC, CD, DA có đồng quy hay không?
Cho tứ giác ABCD, biết rằng các đường trung trực của ba đoạn thẳng AB, AC, AD đồng quy tại một điểm. Hãy giải thích vì sao ABCD là tứ giác nội tiếp.
Đa giác nào dưới đây không nội tiếp một đường tròn?
A. Đa giác đều.
B. Hình chữ nhật.
C. Hình bình hành.
D. Tam giác.
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.
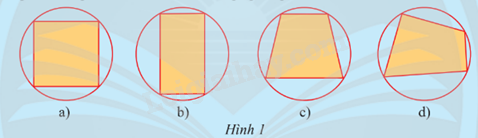
Các tứ giác trong Hình 1 có đặc điểm gì giống nhau?
Vẽ một tứ giác nội tiếp hình tròn và một tứ giác không nội tiếp đường tròn.
Có nhận xét gì về tứ giác trong hình hoa văn trang trí mặt lưng của chiếc ghế với đường tròn trong Hình 3.

Cho tam giác nhọn ABC. Gọi A’, B’, C’ lần lượt là chân đường cao kẻ từ A, B, C và H là trực tâm của tam giác đó. Hãy chỉ ra các tứ giác nội tiếp trong hình.
Tứ giác ở hình nào dưới đây là tứ giác nội tiếp đường tròn (O)?
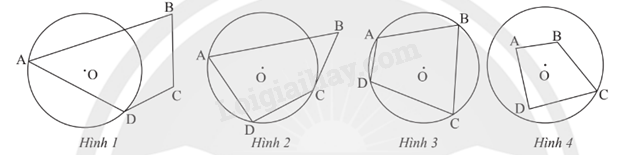
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Trong các phát biểu sau, phát biểu nào đúng?
A. Mọi tứ giác luôn nội tiếp đường tròn.
B. Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 90o.
C. Tổng số đo hai góc đối của một tứ giác nội tiếp luôn bằng 180o.
D. Tất cả các hình thang đều là tứ giác nội tiếp.
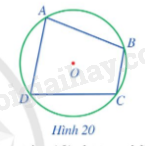
Quan sát Hình 20 và cho biết các đỉnh của tứ giác ABCD có thuộc đường tròn (O) hay không?
Dùng thước thẳng và compa vẽ một tứ giác nội tiếp đường tròn theo các bước sau:
- Vẽ một đường tròn
- Vẽ tứ giác có 4 đỉnh thuộc đường tròn.
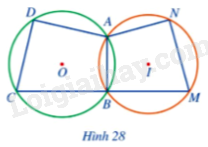
Quan sát Hình 28 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tứ giác ABCD, đường tròn nào ngoại tiếp tứ giác ABMN.
Với các điểm trong Hình 7.12, bạn An cho rằng có thể vẽ một đường tròn đi qua cả bốn điểm A, B, C, D còn bạn Bình thì cho rằng có thể vẽ được một đường tròn đi qua cả bốn điểm A, B, C, E. Hãy vẽ đường tròn đi qua ba điểm A, B, C và cho biết bạn nào đúng.
Vẽ một tứ giác nội tiếp hình tròn và một tứ giác không nội tiếp đường tròn.
Cho tứ giác \(ABCD\) có \(AB\) song song với \(CD\) nội tiếp đường tròn \((O)\). Khi đó tứ giác \(ABCD\) là hình gì?
-
A.
Hình thoi
-
B.
Hình bình hành
-
C.
Hình thang cân
-
D.
Hình thang vuông
Cho điểm \(A\) nằm ngoài đường tròn \(\left( {O;R} \right)\), qua\(A\) kẻ hai tiếp tuyến \(AB\) và \(AC\) với đường tròn (\(B,C\) là các tiếp điểm).
a) Tứ giác \(ABOC\) nội tiếp một đường tròn.
b) \(AO\) là trung trực của đoạn thẳng BC.
c) \(\widehat {ABC} = \widehat {AOC}\).
d) Nếu \(AO = 2R\) thì tam giác \(ABC\) là tam giác đều.
Cho nửa đường tròn tâm (O), đường kính AB = 2R. Đường thẳng qua O và vuông góc AB cắt cung AB tại C. Gọi E là trung điểm BC; AE cắt nửa đường tròn O tại F. Đường thẳng qua C và vuông góc AF tại G cắt AB tại H. Khi đó \(\widehat {OGH}\) có số đo là bao nhiêu độ?
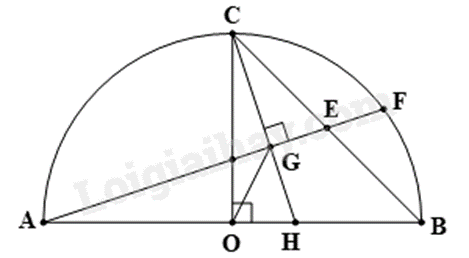
Cho nửa đường tròn tâm \(O,\) đường kính \(AB = 2R.\) Đường thẳng qua \(O\) và vuông góc \(AB\) cắt cung \(AB\) tại \(C.\) Gọi \(E\) là trung điểm \(BC.\,\,AE\) cắt nửa đường tròn \(O\) tại \(F.\) Đường thẳng qua \(C\) và vuông góc $AF$ tại \(G\) cắt \(AB\) tại $H.$ Khi đó góc \(\widehat {OGH}\) có số đo là:
-
A.
\({45^0}\)
-
B.
\({60^0}\)
-
C.
\({90^0}\)
-
D.
\({120^0}\)
Cho tam giác $ABC$ vuông tại $A$ và điểm $D$ nằm giữa $A$ và $B$ . Đường tròn đường kính $BD$ cắt $BC$ tại $E$. Các đường thẳng $CD$ , $AE$ lần lượt cắt đường tròn tại các điểm thứ hai là $F$ và $G$. Khi đó, kết luận không đúng là:
-
A.
$\Delta ABC\backsim\Delta EBD$.
-
B.
Tứ giác $ADEC$ là tứ giác nội tiếp.
-
C.
Tứ giác $AFBC$ không là tứ giác nội tiếp.
-
D.
Các đường thẳng $AC,DE$ và $BF$ đồng quy.
Cho đường tròn $\left( O \right)$ đường kính $AB$. Gọi $I$ là trung điểm của $OA$ . Dây $CD$ vuông góc với $AB$ tại $I$. Lấy $K$ tùy ý trên cung $BC$ nhỏ, $AK$ cắt $CD$ tại $H$. Khẳng định nào đúng ?
-
A.
Tứ giác $BIHK$ nội tiếp.
-
B.
Tứ giác $BIHK$ không nội tiếp.
-
C.
Tứ giác $BIHK$ là hình chữ nhật.
-
D.
Các đáp án trên đều sai.
Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \(\left( O \right),\) các đường cao \(AD,\,BE,\,CF\,\left( {D \in BC,\,E \in AC,\,F \in AB} \right)\) cắt nhau tại \(H\). Khi đó ta có
-
A.
\(BH.BE = BC.BD\)
-
B.
\(CH.CF = CD.CB\)
-
C.
\(A,B\) đều đúng
-
D.
\(A,B\) đều sai
Cho đường tròn $(O)$ đường kính $AB.$ Gọi $H$ là điểm nằm giữa $O$ và $B.$ Kẻ dây $CD$ vuông góc với $AB$ tại $H$. Trên cung nhỏ $AC$ lấy điểm $E,$ kẻ $CK \bot AE$ tại $K.$ Đường thẳng $DE$ cắt $CK$ tại $F.$
Cho tam giác $ABC$ nhọn nội tiếp đường tròn $\left( O \right)$ . $M$ là điểm thuộc cung nhỏ $AC$ (cung \(CM < \) cung \(AM\)). Vẽ $MH$ vuông góc với $BC$ tại $H$ , vẽ $MI$ vuông góc với $AC$ tại $I$ . Chọn câu đúng:
-
A.
$MIHC$ là hình chữ nhật.
-
B.
$MIHC$ là hình vuông.
-
C.
$MIHC$ không là tứ giác nội tiếp.
-
D.
$MIHC$ là tứ giác nội tiếp.
Cho hình bình hành \(ABCD.\) Đường tròn đi qua ba đỉnh \(A,\,B,\,C\) cắt đường thẳng \(CD\) tại \(P\,\,\left( {P \ne C} \right).\) Khi đó
-
A.
\(ABCP\) là hình thang cân
-
B.
\(AP = AD\)
-
C.
\(AP = BC\)
-
D.
Cả \(A,\,B,\,C\) đều đúng
Tìm phát biểu sai trong các phát biểu sau:
a) Tứ giác có bốn đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn.
b) Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc bất kì bằng 180o.
c) Hình chữ nhật luôn nội tiếp đường tròn.
d) Mỗi hình vuông là tứ giác nội tiếp đường tròn
Cho tam giác ABC cân ở A, H là trung điểm của BC và \(\widehat {BAC} < {90^o}\). Đường vuông góc với AB tại A cắt đường thẳng BC ở D. Kẻ DE vuông góc với AC. Chứng minh:
a) AH = EH
b) \(\widehat {DCE} = \widehat {ABD}\).
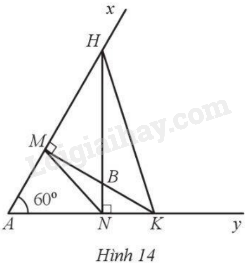
Cho \(\widehat {xAy} = {60^o}\) và điểm B nằm trong góc xAy. Kẻ đường thẳng BN vuông góc với Ay cắt Ax tại H; kẻ đường thẳng BM vuông góc với Ax cắt Ay tại K (Hình 14). Chứng minh:
a) Các tứ giác AMBN, HMNK là các tứ giác nội tiếp đường tròn.
b) HK = 2MN







Danh sách bình luận