Cho góc $\alpha  \in \left( {\frac{{3\pi }}{2};2\pi } \right)$.

Tính giá trị của các biểu thức sau:

a) $A = \frac{{\sin \frac{\pi }{{15}}\cos \frac{\pi }{{10}} + \sin \frac{\pi }{{10}}\cos \frac{\pi }{{15}}}}{{\cos \frac{{2\pi }}{{15}}\cos \frac{\pi }{5} - \sin \frac{{2\pi }}{{15}}\sin \frac{\pi }{5}}}$;                                b) $B = \sin \frac{\pi }{{32}}\cos \frac{\pi }{{32}}\cos \frac{\pi }{{16}}\cos \frac{\pi }{8}$.

Cho $\tan \left( {a + b} \right) = 3,\,\tan \left( {a - b} \right) = 2$.

Tính: $\tan 2a,\,\,\tan 2b$

Cho $\sin a = \frac{2}{{\sqrt 5 }}$. Tính: $\cos 2a,\,\cos 4a$

Cho $\sin a + \cos a = 1$. Tính: $\sin 2a$

Cho $\cos 2a = \frac{1}{3}$ với $\frac{\pi }{2} < a < \pi$. Tính $\sin a,\,\,\cos a,\,\,\tan a$

Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12m. Biết rằng hai sợi cáp trên cũng được gắn với mặt đất tại một vị trí cách chân cột 15m (Hình 18)

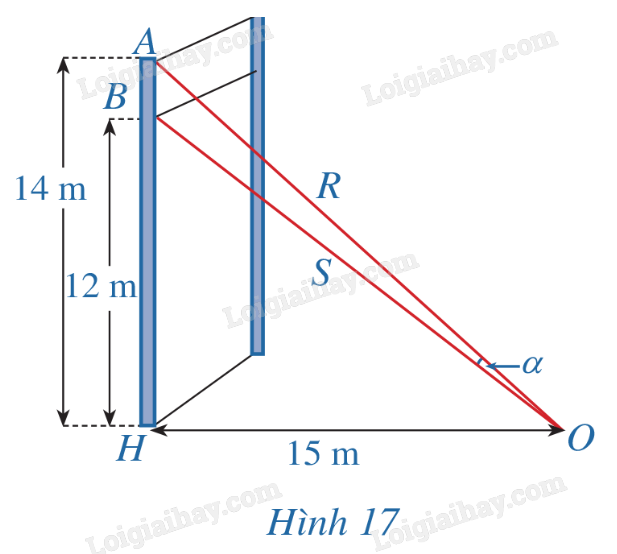
a)     Tính $\tan \alpha$, ở đó $\alpha$ là góc giữa hai sợi cáp trên

b)     Tìm góc $\alpha$ (làm tròn đến kết quả hàng đơn vị theo đơn vị độ)

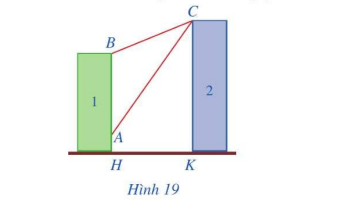
Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là $HK = 20m$. Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được (Hình 19). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là $CK = 32m,AH = 6m,BH = 24m$ (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Nếu $\tan \left( {a + b} \right) = 3,\tan \left( {a - b} \right) =  - 3$ thì $\tan 2a$ bằng:

A. 0

B. $\frac{3}{5}$

C. 1

D. $- \frac{3}{4}$

Nếu $\cos a = \frac{3}{5}$ và $\cos b =  - \frac{4}{5}$ thì $\cos \left( {a + b} \right)\cos \left( {a - b} \right)$ bằng:

A.0

B.2

C.4

D.5

Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?

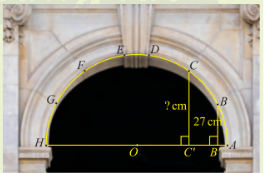
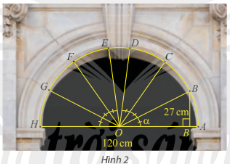
Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính $\sin \alpha$ và $\cos \alpha$, từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.

Tính các giá trị lượng giác của góc 2$\alpha$, biết:

a, $\sin \alpha  = \frac{{\sqrt 3 }}{3},0 < \alpha  < \frac{\pi }{2}$

b, $\sin \frac{\alpha }{2} = \frac{3}{4},\pi  < \alpha  < 2\pi$

Rút gọn các biểu thức sau:

a, $\sqrt 2 \sin \left( {\alpha  + \frac{\pi }{4}} \right) - cos\alpha$,

b, ${\left( {cos\alpha  + \sin \alpha } \right)^2} - \sin 2\alpha$

Tính các giá trị lượng giác của góc $\alpha$, biết:

a, $cos2\alpha  = \frac{2}{5}, - \frac{\pi }{2} < \alpha  < 0$

b, $\sin 2\alpha  =  - \frac{4}{9},\frac{\pi }{2} < \alpha  < \frac{{3\pi }}{4}$

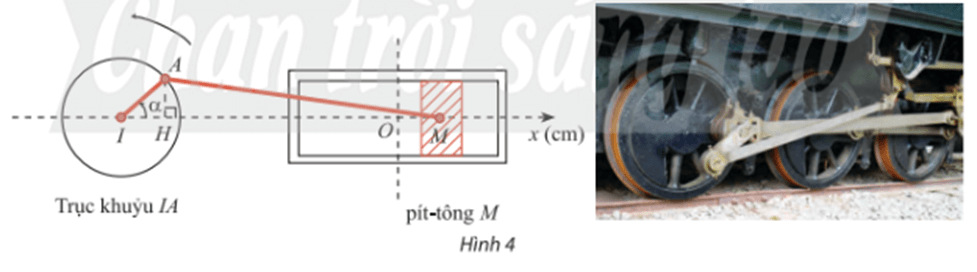
Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho $\alpha$ là góc quay của trục khuỷu, O là vị trí của pít – tông khi $\alpha  = \frac{\pi }{2}$ và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.

a) Biết IA = 8cm, viết công thức tính tọa độ ${x_M}$của điểm M trên trục Ox theo $\alpha$.

b) Ban đầu $\alpha  = 0$. Sau 1 phút chuyển động, ${x_M}$= – 3cm. Xác định${x_M}$ sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười

Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là $\frac{{2\pi }}{3}$ và số đo góc (OA, OM) là $\alpha$.

a) Tính sin$\alpha$ và cos $\alpha$.

b) Tính sin của các góc lượng giác (OA, ON) và (OA, OP) từ đó tính chiều cao của các điểm N và P so với mặt đất (theo đơn vị mét). Làm tròn kết quả đến hàng phần trăm.

Cho $cos\alpha  = \frac{1}{3}$ và $- \frac{\pi }{2} < \alpha  < 0$. Tính

$\begin{array}{l}a)\;sin\alpha \\b)\;sin2\alpha \\c)\;cos\left( {\alpha  + \frac{\pi }{3}} \right)\end{array}$

Chứng minh đẳng thức lượng giác:

$\begin{array}{l}a)\;sin(\alpha  + \beta ).sin(\alpha  - \beta ) = si{n^2}\alpha  - si{n^2}\beta \\b)\;co{s^4}\alpha  - co{s^4}\left( {\alpha  - \frac{\pi }{2}} \right) = cos2\alpha \end{array}$

Cho $\cos 2x =  - \frac{4}{5}$ với $\frac{\pi }{4} < x < \frac{\pi }{2}$

Tính $\sin x,\cos x,\sin \left( {x + \frac{\pi }{3}} \right),\cos \left( {2x - \frac{\pi }{4}} \right)$.

Tính giá trị các biểu thức sau:

a) $A = \sin \frac{\pi }{9} - \sin \frac{{5\pi }}{9} + \sin \frac{{7\pi }}{9}$;                         

b) $B = \sin {6^0}\sin {42^0}\sin {66^0}\sin {78^0}$.

Cho $\cos \alpha  = \frac{3}{4},\,\sin \alpha  > 0;\,\,\sin \beta  = \frac{3}{5};\,\beta  \in \left( {\frac{{9\pi }}{2};5\pi } \right)$.

Hãy tính $\cos 2\alpha ,\,\,\sin 2\alpha ,\,\,\cos 2\beta ,\,\,\sin 2\beta ,\,\,\cos (\alpha  + \beta ),\,\,\sin (\alpha  - \beta )$.

Rút gọn các biểu thức sau

a) $\frac{{\sin ({{45}^0} + \alpha ) - \cos ({{45}^0} + \alpha )}}{{\sin ({{45}^0} + \alpha ) + \cos ({{45}^0} + \alpha )}}$;                    

b) $\frac{{\sin 2\alpha  + \sin \alpha }}{{1 + \cos 2\alpha  + \cos \alpha }}$;

c) $\frac{{1 + \cos \alpha  - \sin \alpha }}{{1 - \cos \alpha  - \sin \alpha }}$;

d) $\frac{{\sin \alpha  + \sin 3\alpha  + \sin 5\alpha }}{{\cos \alpha  + \cos 2\alpha  + \cos 5\alpha }}$.

Chứng minh các biểu thức sau không phụ thuộc vào x

a) $A = \sin \left( {\frac{\pi }{4} + x} \right) - \cos \left( {\frac{\pi }{4} - x} \right)$;           

b) $B = \cos \left( {\frac{\pi }{6} - x} \right) - \sin \left( {\frac{\pi }{3} + x} \right)$;

c) $C = {\sin ^2}x + \cos \left( {\frac{\pi }{3} - x} \right)\cos \left( {\frac{\pi }{3} + x} \right)$;               

d) $D = \frac{{1 - \cos 2x + \sin 2x}}{{1 + \cos 2x + \sin 2x}}.\cot x$.

Hai sóng âm có phương trình lần lượt là

${f_1}\left( t \right) = C\sin \omega t$ và ${f_2}\left( t \right) = C\sin \left( {\omega t + \alpha } \right)$.

Hai sóng này giao thoa với nhau tạo ra một âm kết hợp có phương trình

$f(t) = {f_1}\left( t \right) + {f_2}\left( t \right) = C\sin \omega t + C\sin \left( {\omega t + \alpha } \right)$.

a) Sử dụng công thức cộng chỉ ra rằng hàm số f (t) có thể viết được dưới dạng $f(t) = {\rm{A}}\sin \omega t + {\rm{B}}\cos \omega t$, ở đó A, B là hai hằng số phụ thuộc vào $\alpha$.

b) Khi $C = 10$ và $\alpha  = \frac{\pi }{3}$, hãy tìm biên độ và pha ban đầu của sóng âm kết hợp, tức là tìm hai hằng số $k$ và $\varphi$ sao cho $f(t) = k\sin \left( {\omega t + \varphi } \right)$.

Cho $\sin a = \frac{2}{3}$ với $\frac{\pi }{2} < a < \pi$. Tính:

a) $\cos a$, $\tan a$

b) $\sin \left( {a + \frac{\pi }{4}} \right)$, $\cos \left( {a - \frac{{5\pi }}{6}} \right)$, $\tan \left( {a + \frac{{2\pi }}{3}} \right)$

c) $\sin 2a$, $\cos 2a$

Cho $\cos a = 0,2$ với $\pi  < a < 2\pi$. Tính $\sin \frac{a}{2}$, $\cos \frac{a}{2}$, $\tan \frac{a}{2}$.

Cho $\tan \frac{a}{2} = \frac{1}{{\sqrt 2 }}$. Tính $\sin a$, $\cos a$, $\tan a$.

Trên một mảnh đất hình vuông $ABCD$, bác An đặt một chiếc đèn pin tại vị trí $A$ chiếu chùm sáng phân kì sang phía góc $C$. Bác An nhận thấy góc chiếu sáng của đèn pin giới hạn bởi hai tia $AM$ và $AN$, ở đó các điểm $M$, $N$ lần lượt thuộc các cạnh $BC$, $CD$ sao cho $BM = \frac{1}{2}BC$, $DN = \frac{1}{3}DC$ (xem hình vẽ).

a) Tính $\tan \left( {\widehat {BAM} + \widehat {DAN}} \right)$.

b) Góc chiếu sáng của đèn pin bằng bao nhiêu độ?