Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình sau:

  

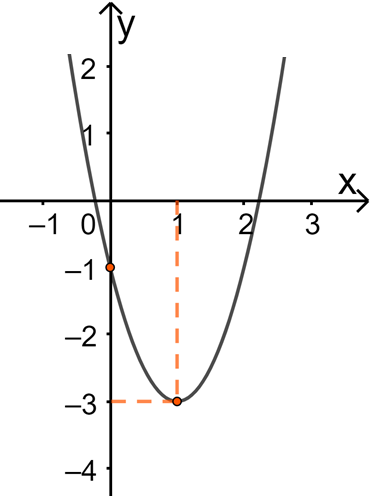
Phương trình của parabol này là

A. \(y =  - {x^2} + x - 1\).

B. \(y = 2{x^2} + 4x + 1\).

C. \(y = {x^2} - 2x - 1\).

D. \(y = 2{x^2} - 4x - 1\).

Đồ thị hàm số cắt trục tung tại điểm \(\left( {0\,\,;\,\, - 1} \right)\) nên \(c =  - 1\).

Tọa độ đỉnh \(I\left( {1\,\,;\, - 3} \right)\), ta có phương trình: \(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 1\\a{.1^2} + b.1 - 1 =  - 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b =  - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b =  - 4\end{array} \right.\).

Vậy parabol cần tìm là: \(y = 2{x^2} - 4x - 1\).

Chọn D