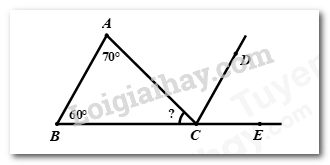
Cho hình vẽ bên dưới. Biết \(AB//CD\)\(,\angle A = {70^0},\angle B = {60^0}.\) Tính số đo của góc \(ACB?\)
A. \(\angle ACB = {70^0}\)
B. \(\angle ACB = {60^0}\)
C. \(\angle ACB = {130^0}\)
D. \(\angle ACB = {50^0}\)
Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song với nhau thì hai góc ở vị trí so le trong bằng nhau; hai góc ở vị trí đồng vị bằng nhau.
Hai góc kề bù có tổng số đo góc bằng \({180^0}\).
Vì \(AB//CD\) nên ta có:
\(\angle BAC = \angle ACD = {70^0}\) (hai góc so le trong)
\(\angle ABC = \angle DCE = {60^0}\) (hai góc đồng vị)
Ta có: \(\angle ACD\) và \(\angle DCE\) là hai góc kề nhau nên \(\angle ACE = \angle ACD + \angle DCE = {70^0} + {60^0} = {130^0}\)
Ta có: \(\angle ACB\) và \(\angle ACE\) là hai góc kề bù nên \(\angle ACB + \angle ACE = {180^0}\)
\(\begin{array}{l} \Rightarrow \angle ACB + {130^0} = {180^0}\\ \Rightarrow \angle ACB = {180^0} - {130^0} = {50^0}\end{array}\)
Vậy \(\angle ACB = {50^0}\)
Chọn D.
