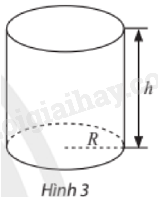
Một người muốn làm một thùng chứa hình trụ có nắp, có dung tích 500 dm3. Cần chọn bán kính đáy và chiều cao của thùng bằng bao nhiêu để tiết kiệm nguyên liệu nhất? Biết đáy và mặt xung quanh của thùng có độ dày như nhau và xác định trước.
• Tìm mối quan hệ giữa \(R,h\), biểu thị diện tích thùng thông qua các đại lượng đã biết và ẩn.
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Thể tích của bể là: \(V = \pi {R^2}h\left( {d{m^3}} \right)\).
Do bể có thể tích 500 dm3 nên ta có: \(\pi {R^2}h = 500 \Rightarrow h = \frac{{500}}{{\pi {R^2}}}\).
Diện tích toàn phần của thùng là: \(S = 2\pi Rh + 2\pi {R^2} = 2\pi R.\frac{{500}}{{\pi {R^2}}} + 2\pi {R^2} = \frac{{1000}}{R} + 2\pi {R^2}\).
Xét hàm số \(S\left( R \right) = \frac{{1000}}{R} + 2\pi {R^2}\) trên khoảng \(\left( {0; + \infty } \right)\).
Ta có: \(S'\left( R \right) = - \frac{{1000}}{{{R^2}}} + 4\pi R\)
\(S'\left( R \right) = 0 \Leftrightarrow - \frac{{1000}}{{{R^2}}} + 4\pi R = 0 \Leftrightarrow \frac{{1000}}{{{R^2}}} = 4\pi R \Leftrightarrow R = \sqrt[3]{{\frac{{250}}{\pi }}}\).
Bảng biến thiên của hàm số trên khoảng \(\left( {0; + \infty } \right)\):
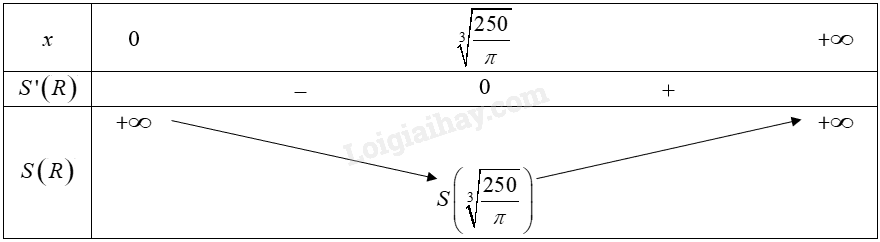
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} S\left( R \right) = S\left( {\sqrt[3]{{\frac{{250}}{\pi }}}} \right)\).
Vậy để tiết kiệm nguyên liệu nhất, cần chọn bán kính \(R = \sqrt[3]{{\frac{{250}}{\pi }}} \approx 4,3\left( {dm} \right)\) và chiều cao\(h = \frac{{500}}{{\pi .{{\left( {\sqrt[3]{{\frac{{250}}{\pi }}}} \right)}^2}}} \approx 8,6\left( {dm} \right)\).

Các bài tập cùng chuyên đề
Mặt cắt ngang của một máng dẫn nước là một hình thang cân có độ dài đáy bé bằng độ dài cạnh bên và bằng \(a\left( {cm} \right)\) không đổi (Hình 5). Gọi \(\alpha \) là một góc của hình thang cân tạo bởi đáy bé và cạnh bên \(\left( {\frac{\pi }{2} \le \alpha < \pi } \right)\). Tìm \(\alpha \) để diện tích mặt cắt ngang của máng lớn nhất.
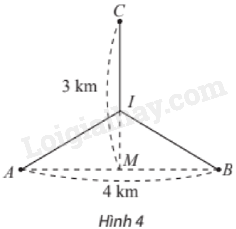
Hai nhà máy được đặt tại các vị trí \(A\) và \(B\) cách nhau 4 km. Nhà máy xử lí nước thải được đặt ở vị trí \(C\) trên đường trung trực của đoạn thẳng \(AB\), cách trung điểm \(M\) của đoạn thẳng \(AB\) một khoảng là 3 km. Người ta muốn làm đường ống dẫn nước thái từ hai nhà máy \(A,B\) đến nhà máy xử lí nước thải \(C\) gồm các đoạn thẳng \(AI,BI\) và \(IC\), với \(I\) là vị trí nằm giữa \(M\) và \(C\) (Hình 4). Cần chọn vị trí điểm \(I\) như thế nào để tổng độ dài đường ống nhỏ nhất? Tìm giá trị nhỏ nhất đó.
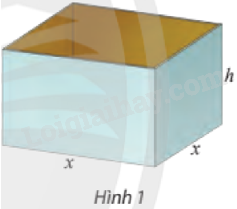
Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp, có đáy là hình vuông và thể tích chứa là \(500d{m^3}\) (Hình 1). Biết rằng chiều cao của thùng trong khoảng từ \(3dm\) đến \(10dm\).
a) Nếu gọi độ dài cạnh đáy của thùng là \(x\left( {dm} \right)\), chiều cao của thùng là \(h\left( {dm} \right)\) thì tổng diện tích các mặt của thùng, kí hiệu \(S\), có thể được biểu thị bằng biểu thức nào?
b) Có thể biểu thị tổng diện tích \(S\) theo \(x\) không? Biến \(x\) nhận giá trị trong miền nào?
c) Với giá trị nào của \(x\) thì \(S\) có giá trị nhỏ nhất?
Hiện tại, mỗi tháng một cửa hàng đồ lưu niệm bán được 100 sản phẩm A. Với mỗi sản phẩm A bán được, cửa hàng thu được 20 nghìn đồng lợi nhuận. Qua khảo sát, người ta thấy rằng với mỗi nghìn đồng giảm giá, cửa hàng bán thêm được 10 sản phẩm A. Cửa hàng nên giảm giá bao nhiêu cho mỗi sản phẩm A để thu được lợi nhuận lớn nhất từ việc bán sản phẩm này? Tính lợi nhuận lớn nhất đó.
Cơ sở A chuyên cung cấp một loại sản phẩm nông nghiệp X cho nhà phân phối B. Hai bên thoả thuận rằng, nếu đầu tháng B đặt hàng 1 tạ sản phẩm X thì giá bán mỗi tạ sản phẩm là \(P\left( x \right) = 5 - 0,0005{x^2}\) (triệu đồng) \(\left( {x \le 40} \right)\). Chi phí A phải bỏ ra cho \(x\) tạ sản phẩm X trong một tháng là \(C\left( x \right) = 10 + 3,5x\) (triệu đồng).
a) Nếu trong một tháng A bán \(x\) tạ sản phẩm X cho B thì A nhận được bao nhiêu doanh thu, bao nhiêu lợi nhuận?
b) Trong một tháng B đặt hàng bao nhiêu tạ sản phẩm X từ A thì A nhận được lợi nhuận lớn nhất?
Tại một xưởng sản xuất, chi phí để sản xuất \(x\) sản phẩm mỗi tháng là
\(C\left( x \right) = 5000 + 50x + 0,005{x^2}\) (nghìn đồng).
a) Tính chi phí trung bình để sản xuất một sản phẩm.
b) Mỗi tháng xưởng sản xuất bao nhiêu sản phẩm thì chi phí trung bình để sản xuất một sản phẩm thấp nhất?
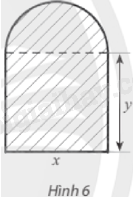
Người ta muốn xây một đường cống thoát nước có mặt cắt ngang là hình tạo bởi một nửa hình tròn ghép với một hình chữ nhật (Hình 6). Biết rằng mặt cắt ngang có diện tích 2 m2. Các kích thước \(x,y\) (đơn vị: m) bằng bao nhiêu để chu vi của mặt cắt ngang là nhỏ nhất? Tính chu vi nhỏ nhất đó.
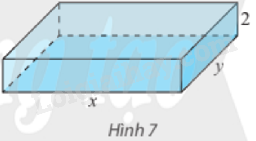
Người ta muốn xây một bể bơi có dạng hình hộp chữ nhật, thể tích 1800 m3 và chiều sâu 2 m (Hình 7). Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Cần chọn chiều dài và chiều rộng của bể bằng bao nhiêu để tiết kiệm chi phí xây dựng bể nhất?
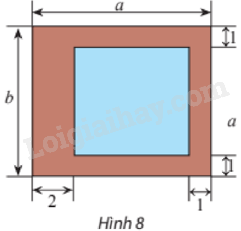
Người ta muốn thiết kế một lồng nuôi cá có bề mặt hình chữ nhật bao gồm phần mặt nước có diện tích bằng 54 m2 và phần đường đi xung quanh với kích thước (đơn vị: m) như Hình 8. Bề mặt của lồng có chiều dài và chiều rộng bằng bao nhiêu để diện tích phần đường đi là bé nhất?
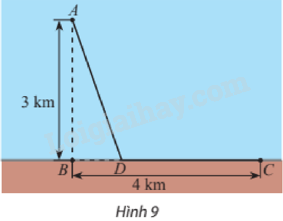
Một giếng dầu ngoài khơi được đặt ở vị trí \(A\) cách bờ biển 3 km, \(B\) là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí \(C\) trên bờ biển, cách vị trí \(B\) một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng \(AD\) và \(DC\) (\(D\) là một vị trí nằm giữa \(B\) và \(C\)). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của \(D\) như thế nào để giảm thiểu chi phí lắp đặt nhất?
Tại một xí nghiệp, nếu trong một tuần xí nghiệp sản xuất \(x\) nghìn sản phẩm thì chi phí sản xuất gồm: 10 triệu đồng chi phí cố định, 3 triệu đồng cho mỗi nghìn sản phẩm và \(0,001{x^2}\) triệu đồng chi phí bảo dưỡng thiết bị.
a) Tính chi phí trung bình trên mỗi nghìn sản phẩm theo \(x\).
b) Mỗi tuần xí nghiệp cần sản xuất bao nhiêu sản phẩm để chi phí trung bình thấp nhất?
Một người muốn làm một bể chứa hình hộp chữ nhật không nắp có thể tích 4 m3, chiều cao 1 m. Biết rằng chi phí làm đáy bể là 3 triệu đồng/m2, chi phí làm thành bể là 2 triệu đồng/m2. Chi phi tối thiểu để làm bể là
A. 20.
B. 24.
C. 28.
D. 32.
Chi phí để sản xuất \(x\) sản phẩm là \(C\left( x \right) = 2500 + 10x + \frac{1}{4}{x^2}\) (nghìn đồng). Chi phí trung bình trên mỗi sản phẩm là thấp nhất khi số lượng sản phẩm được sản xuất là
A. 20.
B. 50.
C. 100.
D. 1000.
Cho mạch điện có sơ đồ như Hình 4. Nguồn điện có suất điện động \(E = 4V\) và điện trở trong \(r = 2{\Omega }\). Điện trở ở mạch ngoài là \(R\left({\Omega } \right)\) thay đổi. Cường độ dòng điện \(I\left( A \right)\) chạy trong mạch và công suất \(P\left( W \right)\) của dòng điện ở mạch ngoài được tính lần lượt theo các công thức
\(I = \frac{E}{{r + R}}\) và \(P = {I^2}R\)
(Vật lí 11, Nhà xuất bản Giáo dục Việt Nam, 2012, trang 49, 51).
Điện trở \(R\) bằng bao nhiêu thì công suất \(P\) có giá trị lớn nhất? Tính giá trị lớn nhất đó.
Theo kết quả thăm dò trước một buổi biểu diễn văn nghệ ngoài trời, nếu giá bán mỗi vé là \(p\) nghìn đồng thì sẽ có \({\rm{x}}\) người mua vé xem biểu diễn, giữa \(p\) và \({\rm{x}}\) có mối liên hệ: \(p = 500.{e^{ - 0,0005x}}\). Đơn vị tổ chức nên bán vé với giá bao nhiêu thì đạt được doanh thu (tổng số tiền bán vé) cao nhất?
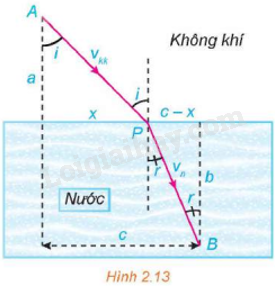
Gọi \({v_{kk}}\) là vận tốc ánh sáng trong không khí và \({v_n}\) là vận tốc ánh sáng trong nước. Theo nguyên lí Fermat, một tia sáng di chuyển từ một điểm A trong không khí đến một điểm B trong nước theo đường gấp khúc APB sao cho tổng thời gian di chuyển là nhỏ nhất (Hình 2.13). Vận dụng đạo hàm tìm vị trí cực trị của hàm số T(x) (tổng thời gian tia sáng đi từ A đến B theo đường gấp khúc APB) để chứng tỏ rằng khi T(x) nhỏ nhất thì góc tới i và góc khúc xạ r thỏa mãn phương trình \(\frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}\).
Phương trình này được gọi là Định luật Snell.
Một vật được ném từ mặt đất lên trời xiên góc \(\alpha \) với phương nằm ngang với vận tốc ban đầu \({v_0}\; = 9{\rm{ }}m/s\)(Hình 2.10). Khi đó quỹ đạo chuyển động của vật tuân theo phương trình \(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) , ở đó x (mét) là khoảng cách vật bay được theo phương ngang từ điểm ném, y (mét) là độ cao so với mặt đất của vật trong quá trình bay, g là gia tốc trọng trường (theo Vật lí đại cương, Nhà xuất bản Giáo dục Việt Nam, 2016).
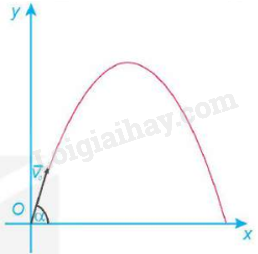
a) Tính độ cao nhất của vật trên quỹ đạo và xác định thời điểm mà vật đạt được độ cao đó (giả sử gia tốc trọng trường là g = 9,8 m/s2).
b) Xác định góc ném α để tầm ném xa của vật đạt giá trị lớn nhất.
Một người đánh cá đang ở trên thuyền (vị trí A) cách bờ biển (điểm P) 2 km về phía đông trên đường bờ biển thẳng theo phương bắc nam. Nhà anh ấy nằm bên bờ biển, cách vị trí điểm P khoảng 6 km về phía bắc. Anh ấy có thể chèo thuyền với vận tốc 3 km/h và đi bộ với vận tốc 5 km/h (giả sử vận tốc của dòng nước là không đáng kể so với vận tốc mà người đánh cá chèo thuyền). Anh ấy dự kiến sẽ chèo thuyền thẳng đến một điểm Q đâu đó trên bờ biển về phía bắc điểm P, với 0 ≤ PQ ≤ 6 (km), rồi đi bộ quãng đường còn lại để về nhà.
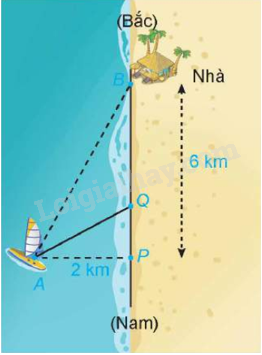
a) Hãy chọn các kí hiệu cho các đại lượng đã biết và đại lượng chưa biết trong bài toán trên.
b) Tìm các mối quan hệ giữa các kí hiệu trong câu a).
c) Nếu anh ấy chèo thuyền đến P rồi đi bộ về nhà thì hết bao nhiêu thời gian?
d) Nếu anh ấy chèo thuyền đến điểm Q, rồi đi bộ về nhà thì hết bao nhiêu thời gian?
Biết rằng \(C\left( x \right) = 16{\rm{ }}000 + 500x--1,64{x^2} + 0,004{x^3}\;\)là hàm chi phí và \(p\left( x \right) = 1{\rm{ }}700--7x\) là hàm cầu của x đơn vị hàng hóa. Hãy tìm mức sản xuất để lợi nhuận là lớn nhất.
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay, doanh nghiệp đang tập trung chiến lược kinh doanh một loại xe máy với chi phí mua vào là 27 triệu đồng/chiếc và giá bán ra là 31 triệu đồng/chiếc. Với giá bán này thì số lượng xe bán ra mỗi năm là 600 chiếc. Nhằm tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán. Ước tính rằng cứ giảm 1 triệu đồng/chiếc thì số lượng xe bán ra trong một năm tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để thu được lợi nhuận là cao nhất?
Một cửa sổ có dạng hình phía dưới là hình chữ nhật, phía trên là nửa hình tròn có đường kính bằng chiều rộng của hình chữ nhật (Hình 2.17). Biết độ dài mép ngoài của cửa sổ, phần sát tường (kể cả phần nửa đường tròn phía trên) là 10 m. Hãy tính các kích thước của hình chữ nhật để cửa sổ có diện tích lớn nhất (kết quả làm tròn đến chữ số thập phân thứ hai).

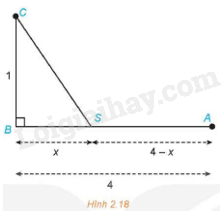
Người ta muốn kéo một đường dây điện tử nhà máy điện đặt tại điểm A đến một hòn đảo nhỏ C. Biết rằng nhà máy điện nằm sát bờ biển, bờ biển được coi là thẳng, khoảng cách CB từ hòn đảo C đến bờ biển là 1 km, khoảng cách giữa hai điểm A và B là 4 km. Mỗi kilômét dây nếu đặt ngầm dưới nước sẽ mất 5 000 USD, còn nếu đặt ngầm dưới đất sẽ mất 3 000 USD. Người ta dự định kéo dây điện ngầm dưới đất từ điểm A đến một điểm S trên bờ biển, nằm giữa A và B, sau đó chạy ngầm dưới nước từ điểm S đến hòn đảo C (Hình 2.18). Tìm vị trí điểm S sao cho chi phí kéo đường dây là nhỏ nhất.
Một xe khách tuyến có sức chứa tối đa là 60 hành khách. Nếu chuyến xe chở x hành khách thì giá mỗi hành khách là \(50{\rm{ }}000{\left( {3 - \frac{x}{{40}}} \right)^2}\)(đồng). Xe có doanh thu cao nhất khi chở bao nhiêu hành khách, và doanh thu đó bằng bao nhiêu?
Một công ty dự kiến chi 1 tỉ đồng sản xuất các thùng đựng sơn hình trụ với dung tích \(5{\rm{ }}l\). Giá sản xuất mặt xung quanh là 100 nghìn đồng/m2, giá sản xuất mặt đáy là 120 nghìn đồng/m2. Hỏi công ty có thể sản xuất được tối đa bao nhiêu thùng sơn? (Giả sử chi phí cho các mối nối không đáng kể)
Giả sử \(C\left( x \right) = 18{\rm{ }}000 + 500x--1,6{x^2} + 0,004{x^3}\;\)(nghìn đồng) là hàm chi phí và \(p\left( x \right) = 1{\rm{ }}500--3x\) (nghìn đồng) là hàm cầu của \(x\) đơn vị một loại hàng hóa nào đó.
a) Tìm công thức của hàm lợi nhuận \(P\left( x \right)\), biết rằng hàm lợi nhuận bằng hiệu của hàm doanh thu và hàm chi phí.
b) Tìm mức sản xuất x để lợi nhuận thu được là lớn nhất.
Một vật nặng có khối lượng m được kéo dọc theo mặt phẳng nằm ngang nhờ một sợi dây hợp với phương ngang một góc 0. Trong Vật lí, ta biết rằng lực kéo F cần thiết để di chuyển vật được cho bởi công thức
\(F = \frac{{cmg}}{{c\sin \theta + \cos \theta }}\)
trong đó g là gia tốc trọng trưởng và c là hệ số ma sát của bề mặt (Theo Sullivan and Miranda, Calculus, W.H. Freeman and Company, 2014). Chứng tỏ rằng lực kéo F nhỏ nhất khi \(\tan \theta = c.\)
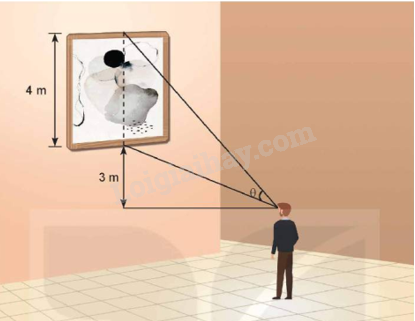
Một bức tranh cao 4 m được treo trên tường có mép dưới cao hơn tầm mắt người quan sát là 3 m (như hình vẽ). Người quan sát phải đứng cách tường bao nhiêu mét để có được tầm nhìn thuận lợi (tức là, có góc nhìn \(\theta \) lớn nhất)?
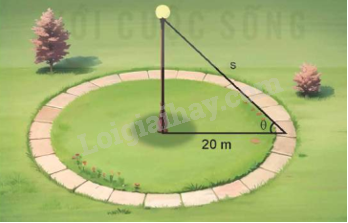
Một khu vực hình tròn có bán kính 20 m được bao quanh bởi một lối đi bộ (như hình vẽ). Một bóng đèn được lắp ở trên đỉnh cột nằm ở trung tâm của khu vực. Hỏi độ cao của cột đèn là bao nhiêu thì sẽ chiếu sáng mạnh nhất cho lối đi bộ? Biết rằng cường độ chiếu sáng cho bởi công thức \(I = \frac{{\sin \theta }}{s}\), trong đó s là khoảng cách từ nguồn sáng và \(\theta \) là góc mà ánh sáng chiếu vào bề mặt.
Giả sử một loại hàng hóa có hàm cầu được mô hình hóa bởi \(p = 100--0,5x\) và hàm chi phí được mô hình hóa bởi \(C = 40x + 37,5\), trong đó p (nghìn đồng) là giá của một đơn vị hàng hóa đó.
a) Mức giá nào sẽ mang lại lợi nhuận lớn nhất?
b) Khi lợi nhuận là lớn nhất, chi phí trung bình cho mỗi đơn vị là bao nhiêu?
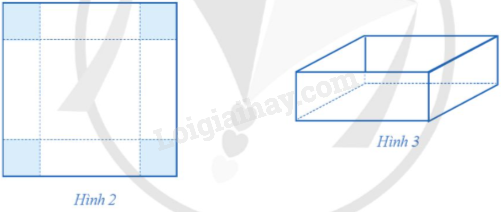
Bạn Hà có một tấm bìa hình vuông cạnh 60 cm (Hình 2). Bạn muốn làm một cái hộp đựng đồ có dạng hình hộp chữ nhật mà có thể để được vào một ngăn sách có dạng hình hộp chữ nhật, đáy là hình vuông cạnh 37 cm, chiều cao bằng 28 cm. Bạn cắt bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x\) (cm), rồi gập lại thành một cái hộp không nắp (Hình 3). Tìm số nguyên dương \(x\) để làm được cái hộp đựng đồ có thể tích lớn nhất.







Danh sách bình luận