Hãy tự thiết kế một cổng chào hình parabol.
Bước 1: Khởi động phần mềm Geogebra đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online
Bước 2: Mở tính năng thanh trượt, nhập các công thức sau
\(y = a{x^2} + bx + c\) vào vùng nhập lệnh bằng cú pháp y = ax^2 + bx + c
\(\Delta = {b^2} - 4ac\) vào vùng nhập lệnh bằng cú pháp D = b^2 – 4ac
Bước 3: Điều chỉnh a, b, c trên thanh trượt cho tới khi được cồng chào như mong muốn
Bước 4: Xác định chiều cao của cổng mong muốn
Khởi động phần mềm Geogebra và mở tính năng thanh trượt.
Nhập các công thức y = ax^2 + bx + c , D = b^2 – 4ac vào vùng lệnh.
Điều chỉnh các thanh trượt ta có parabol như hình dưới.
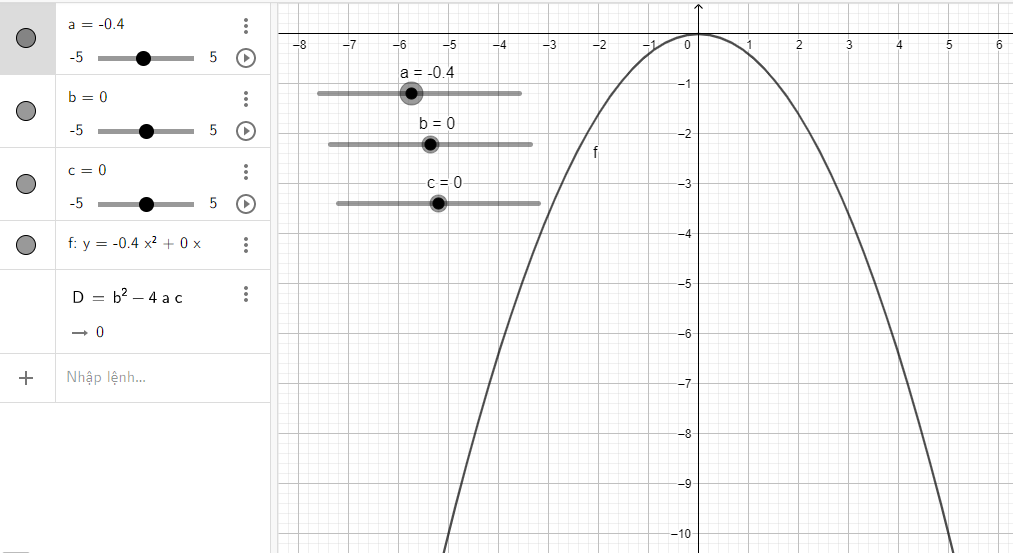
Ta được hình dạng của cổng chào hình parabol.

Các bài tập cùng chuyên đề
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x - 2y + 3 \le 0\\x + 3y > - 2\\x \le 0\end{array} \right.\)
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau:
Vẽ đồ thị các hàm số bậc hai sau:
a) \(y = - {x^2} + 4x - 3\)
b) \(y = {x^2} + 2\)
c) \(y = \frac{1}{2}{x^2} + x + 1\)
d) \(y = {x^2} - 4x + 4\)
Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau:
a) \(\)\(y = {x^2} - 3x + 2\)
b) \(y = {x^2}\)
c) \(y = - {x^2}\)
d) \(y = 2{x^2} + 1\)
e) \(y = - \frac{1}{2}{x^2} + 4\)







Danh sách bình luận