Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và có vectơ chỉ phương \(\overrightarrow u {\rm{ }} = \left( {a;{\rm{ }}b} \right)\). Xét điểm M(x ; y) nằm trên \(\Delta \) (Hình 26).
a) Nhận xét về phương của hai vectơ \(\overrightarrow u {\rm{ }}\)và\(\overrightarrow {{M_o}M} \).
b) Chứng minh có số thực t sao cho \(\overrightarrow {{M_o}M} \) = \(t\overrightarrow u {\rm{ }}\).
c) Biểu diễn toạ độ của điểm M qua toạ độ của điểm \({M_o}\) và toạ độ của vectơ chỉ phương \(\overrightarrow u {\rm{ }}\).
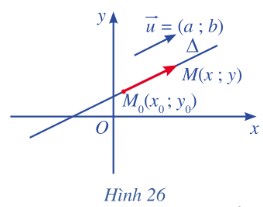
a) Hai vectơ \(\overrightarrow u {\rm{ }}\)và \(\overrightarrow {{M_o}M} \) cùng phương với nhau.
b) Xét \(M\left( {x;y} \right)\). Vì cùng phương với nên có số thực t sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }}\).
c) Do \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\) nên:
\(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }} \Leftrightarrow \left\{ \begin{array}{l}x - {x_o} = at\\y - {y_o} = bt\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = {x_o} + at\\y = {y_o} + bt\end{array} \right.\)
Vậy tọa độ điểm M là: \(M\left( {{x_o} + at;{y_o} + bt} \right)\).

Các bài tập cùng chuyên đề
Lập phương trình tham số của đường thẳng \(\Delta \) đi qua điểm \(M\left( { - 1;2} \right)\) và song song với đường thẳng \(d:3x - 4y - 1 = 0\).
Phương trình nào sau đây là phương trình tham số của đường thẳng?
A. \(2x - y + 1 = 0\)
B. \(\left\{ \begin{array}{l}x = 2t\\y = t\end{array} \right.\)
C. \({x^2} + {y^2} = 1\)
D. \(y = 2x + 3\)
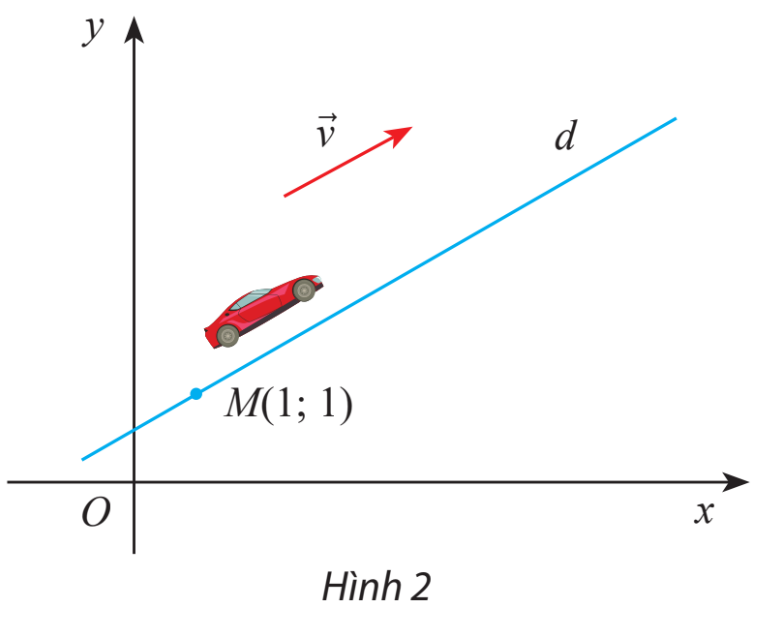
Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm \(M(1;1)\) với vectơ vận tốc\(\overrightarrow v = (40;30)\).
a) Viết phương trình tham số của đường thẳng d biểu diễn đường đi của ô tô.
b) Tìm tọa độ của xe tương ứng với t = 2; t = 4.
a) Viết phương trình tham số của đường thẳng d đi qua điểm \(B( - 9;5)\) và nhận \(\overrightarrow v = (8; - 4)\) là vectơ chỉ phương.
b) Tìm tọa độ điểm P trên \(\Delta \), biết P có tung độ bằng 1.
Cho đường thẳng \(\Delta \) có phương trình tham số \(\left\{ \begin{array}{l}x = 1 - 2t\\y = - 2 + t\end{array} \right.\)
a) Chỉ ra tọa độ của hai điểm thuộc đường thẳng \(\Delta \).
b) Điểm nào trong các điểm \(C( - 1: - 1).{\rm{ }}D\left( {1:3} \right)\) thuộc đường thẳng \(\Delta \)?
Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 3 - t\\y = 4 + 2t\end{array} \right.\). Vectơ nào dưới đây là một vectơ chỉ phương của ∆?
A. \(\overrightarrow {{u_1}} = (3;4)\)
B. \(\overrightarrow {{u_2}} = ( - 2;1)\)
C. \(\overrightarrow {{u_3}} = ( - 1;2)\)
D. \(\overrightarrow {{u_4}} = ( - 2; - 1)\)
Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 - 5t\\y = - 1 + 3t\end{array} \right.\). Trong các điểm có tọa độ dưới đây điểm nào nằm trên đường thẳng ∆?
A. (-3; -2)
B. (2; -1)
C. (-2; 1)
D. (-5; 3)
A. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array}} \right.\).
B. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + at}\\{y = {y_0} - bt}\end{array}} \right.\).
C. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + bt}\\{y = {y_0} + at}\end{array}} \right.\)
D. \(\left\{ {\begin{array}{*{20}{c}}{x = {x_0} - bt}\\{y = {y_0} - at}\end{array}} \right.\).







Danh sách bình luận