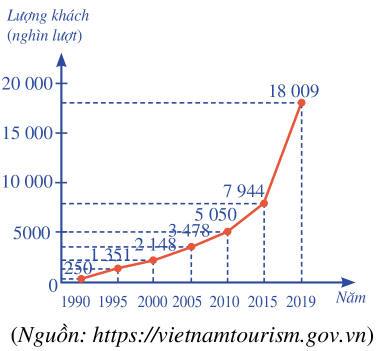
Biểu đồ đoạn thẳng ở Hình 6 cho biết lượng khách du lịch quốc tế đến Việt Nam trong một số năm (từ 1990 đến 2019).
a) Viết mẫu số liệu thống kê số lượt khách du lịch Lượng khách quốc tế đến Việt Nam nhận được từ biểu đồ bên.
b) Viết mẫu số liệu theo thứ tự tăng dần. Tìm số trung bình cộng, trung vị và tứ phân vị của mẫu số liệu đó.
c) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
a) Quan sát biểu đồ
b) Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \({X_1},{X_2},...,{X_n}\)
Bước 2: Số trung bình cộng : \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
Bước 3: Trung vị \({Q_2} = {M_e} = \left\{ \begin{array}{l}{X_{k + 1}}\quad \quad \quad \quad \quad (n = 2k + 1)\\\frac{1}{2}({X_k} + {X_{k + 1}})\quad \;\,(n = 2k)\end{array} \right.\)
\({Q_1}\) là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
\({Q_3}\) là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
c) Khoảng biến thiên: \(R = {X_n} - {X_1}\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
d) Tính phương sai \({s^2} = \frac{1}{n}\left[ {{{\left( {{x_1} - \overline x } \right)}^2} + {{\left( {{x_2} - \overline x } \right)}^2} + ... + {{\left( {{x_n} - \overline x } \right)}^2}} \right]\)
Độ lệch chuẩn \(s = \sqrt {{s^2}} \)
a) Mẫu số liệu thống kê số lượt khách du lịch Lượng khách quốc tế đến Việt Nam nhận được từ biểu đồ bên là:
250 1351 2148 3478 5050 7944 18009
b) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được: 250 1351 2148 3478 5050 7944 18009
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{250{\rm{ + }}1351{\rm{ + }}2148{\rm{ + }}3478{\rm{ + }}5050{\rm{ + }}7944{\rm{ + }}18009}}{7} = \frac{{38230}}{7}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 7 số liệu ( lẻ ) nên trung vị \({Q_2} = 3478\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 250 1351 2148 là: \({Q_1} = 1351\)
- Trung vị của dãy 5050 7944 18009 là: \({Q_3} = 7944\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 1351\), \({Q_2} = 3478\), \({Q_3} = 7944\)
c) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 18009 - 250 = 17759\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 7944 - 1351 = 6593\)
d) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {250 - \overline x } \right)}^2} + {{\left( {351 - \overline x } \right)}^2} + ... + {{\left( {18009 - \overline x } \right)}^2}} \right]}}{7} \approx 31820198,82\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 5640,93\)

Các bài tập cùng chuyên đề
Một hằng số quan trọng trong toán học là số e có giá trị gần đúng với 12 chữ số hập phân là 2,718281828459.
a) Giả sử ta lấy giá trị 2,7 làm giá trị gần đúng của e. Hãy chứng tỏ sai số tuyệt đối không vượt quá 0,02 và sai số tương đối không vượt quá 0,75%
b) Hãy quy tròn e đến hàng phần nghìn.
c) Tìm số gần đúng của số e với độ chính xác 0,00002.
Cho các số gần đúng \(a = 54919020 \pm 1000\) và \(b = 5,7914003 \pm 0,002.\)
Hãy xác định số quy tròn của a và b.
Mỗi học sinh lớp 10A đóng góp 2 quyển sách cho thư viện trường. Lớp trưởng thống kê lại số sách mà mỗi tổ trong lớp đóng góp ở bảng sau:
|
Tổ |
Tổng số sách |
|
1 |
16 |
|
2 |
20 |
|
3 |
20 |
|
4 |
19 |
|
5 |
18 |
Hãy cho biết lớp trưởng thống kê đã chính xác chưa. Tại sao?
Sản lượng nuôi tôm phân theo địa phương của các tỉnh Cà Mau và Tiền Giang được thể hiện ở hai biểu đồ sau (đơn vị: tấn):
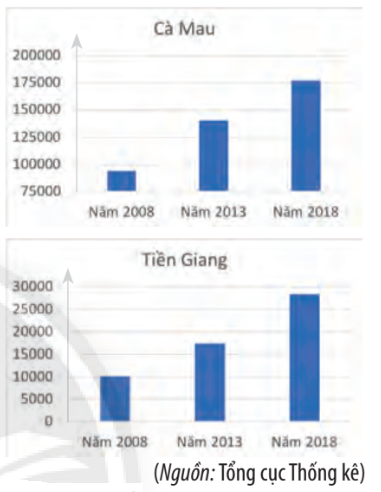
a) Hãy cho biết các phát biểu sau là đúng hay sai?
i. Sản lượng nuôi tôm mỗi năm của tỉnh Tiền Giang đều cao hơn tỉnh Cà Mau.
ii. Ở tỉnh Cà Mau, sản lượng nuôi tôm năm 2018 tăng gấp hơn 4 lần so với năm 2008.
iii. Ở tỉnh Tiền Giang, sản lượng nuôi tôm năm 2018 tăng gấp hơn 2,5 lần so với năm 2008.
iv. Ở tỉnh Tiền Giang, từ năm 2008 đến năm 2018, sản lượng nuôi tôm mỗi năm tăng trên 50% so với năm cũ.
v. Trong vòng 5 năm từ 2013 đến 2018, sản lượng nuôi tôm của tỉnh Cà Mau tăng cao hơn của tỉnh Tiền Giang.
b) Để so sánh sản lượng nuôi tôm của hai tỉnh Cà Mau và Tiền Giang, ta nên sử dụng loại biểu đồ nào?
Bạn Châu cân lần lượt 50 quả vải thiều Thanh Hà được lựa chọn ngẫu nhiên từ vườn nhà mình và được kết quả như sau:
|
Cân nặng (đơn vị: gam) |
Số quả |
|
8 |
1 |
|
19 |
10 |
|
20 |
19 |
|
21 |
17 |
|
22 |
3 |
a) Hãy tìm số trung bình, trung vị, mốt của mẫu số liệu trên
b) Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ của mẫu số liệu trên.
Độ tuổi của 22 cầu thủ ở đội hình xuất phát của hai đội bóng đá được ghi lại ở bảng sau:
|
Đội A |
Đội B |
|
28 |
32 |
|
24 |
20 |
|
26 |
19 |
|
25 |
21 |
|
25 |
28 |
|
23 |
29 |
|
20 |
21 |
|
29 |
22 |
|
21 |
29 |
|
24 |
19 |
|
24 |
29 |
a) Hãy tìm số trung bình, mốt, độ lệch chuẩn và tứ phân vị của tuổi mỗi cầu thủ của từng đội bóng.
b) Tuổi của các cầu thủ ở đội bóng nào đồng đều hơn? Tại sao?
Một cửa hàng bán xe ô tô thay đổi chiến lược kinh doanh vào cuối năm 2019. Số xe của hàng bán được mỗi tháng trong năm 2019 và 2020 được ghi lại ở bảng sau:
|
Tháng |
Năm 2019 |
Năm 2020 |
|
1 |
54 |
45 |
|
2 |
22 |
28 |
|
3 |
24 |
31 |
|
4 |
30 |
34 |
|
5 |
35 |
32 |
|
6 |
40 |
35 |
|
7 |
31 |
37 |
|
8 |
29 |
33 |
|
9 |
29 |
33 |
|
10 |
37 |
35 |
|
11 |
40 |
34 |
|
12 |
31 |
37 |
a) Hãy tính số trung bình, khoảng tứ phân vị và độ lệch chuẩn của số lượng xe bán được trong năm 2019 và năm 2020.
b) Nêu nhận xét về tác động của chiến lược kinh doanh mới lên số lượng xe bán ra hằng tháng.
Hãy tìm phương sai, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ (nếu có) của mỗi mẫu số liệu sau:
a) 90; 56; 50; 45; 46; 48; 52; 43.
b) 19; 11; 1; 16; 19; 12; 14; 10; 11.
c) 6,7; 6,2; 9,7; 6,3; 6,8; 6,1; 6,2.
d) 0,79; 0,68; 0,35; 0,38; 0,05; 0,35.
Khuê và Trọng ghi lại số tin nhắn điện thoại mà mỗi người nhận được từ ngày 1/9 đến ngày 15/9 năm 2020 ở bảng sau:
|
Khuê |
2 |
4 |
3 |
4 |
6 |
2 |
3 |
2 |
4 |
5 |
3 |
4 |
6 |
7 |
3 |
|
Trọng |
3 |
4 |
1 |
2 |
2 |
3 |
4 |
1 |
2 |
30 |
2 |
2 |
2 |
3 |
6 |
a) Hãy tìm phương sai của từng dãy số liệu.
b) Sau khi bỏ đi các giá trị ngoại lệ (nếu có), hãy so sánh số lượng tin nhắn mỗi bạn nhận được theo số trung bình và theo trung vị.
Bình dùng đồng hồ đo thời gian để một vật rơi tự do (đơn vị: giây) từ vị trí A đến vị trí B trong 10 lần kết quả như sau:
|
0,398 |
0,399 |
0,408 |
0,410 |
0,406 |
0,405 |
0,402 |
0,401 |
0,290 |
0,402 |
Bình nghĩ là giá trị 0,290 ở lần đo thứ 9 không chính xác. Hãy kiểm tra nghi ngờ của Bình.
Một nhân viên kiểm tra định kỳ một cột đo xăng dầu, kết quả đo (trong một thời gian nhất định) là 50 lít. Đồng hồ của cột đo xăng dầu báo là 50,3 lít. Theo quy định, sai số lớn nhất đối với kiểm tra định kỳ là 0,5% (Theo Văn bản kỹ thuật đo lường Việt Nam, ĐLVN \(10:2017\)). Giá trị trên đồng hồ của cột đo xăng dầu có nằm trong giới hạn cho phép không?
Z-score là chỉ số được tổ chức y tế thế giới WHO sử dụng để đánh giá tình trạng dinh dưỡng của người thông qua các thông số chiều cao, cận nặng và độ tuổi.
\(Z = \frac{{H - \overline h }}{s}.\)
Trong đó \(\overline h \) là chiều cao trung bình của lứa tuổi, \(s\) là độ lệch chuẩn, \(H\) là chiều cao người đang xét. Nếu \(Z < - 3\) thì người đó suy dinh dưỡng thể thấp còi, mức độ năng; Nếu \( - 3 \le Z < - 2\) thì người đó suy dinh dưỡng thể thấp còi, mức độ vừa.
Hỏi một người 17 tuổi, cao 155cm có bị suy dinh dưỡng thể thấp còi không? Nếu bị thì ở mức độ nào? Biết rằng chiều cao trung bình của nam 17 tuổi là 175,16 cm và độ lệch chuẩn là 7,64 cm (Theo WHO).
Thu nhập theo tháng (đơn vị: triệu đồng) của các công nhân trong một công ty nhỏ được cho như sau:
|
5,5 |
6,0 |
8,0 |
7,0 |
7,5 |
8,0 |
7,0 |
9,5 |
|
12,0 |
10,0 |
4,5 |
11,0 |
13,0 |
9,5 |
8,5 |
4,0 |
a) Tính thu nhập trung bình theo tháng của công nhân công ty này.
b) Trong đại dịch Covid-19 công ty có chính sách hỗ trợ 25% công nhân có thu nhập thấp nhất. Số nào trong các tứ phân vị giúp xác định các công nhân trong diện được hỗ trợ? Tính giá trị tứ phân vị đó.
Số liệu thống kê kết quả 5 bài kiểm tra môn Toán của bạn Dũng là: 8 6 7 5 9 (3) (xem Bảng 4).
Số trung bình cộng của mẫu số liệu (3) là: \(\overline x = \frac{{8 + 6 + 7 + 5 + 9}}{5} = 7\)
a) Tính các độ lệch sau: (8 – 7); (6 – 7); (7 – 7); (5 – 7); (9 – 7).
b) Tính bình phương các độ lệch và tính trung bình cộng của chúng.
Trong 5 lần nhảy xa, hai bạn Hùng và Trung có kết quả (đơn vị: mét) lần lượt là
|
Hùng |
2,4 |
2,6 |
2,4 |
2,5 |
2,6 |
|
Trung |
2,4 |
2,5 |
2,5 |
2,5 |
2,6 |
a) Kết quả trung bình của hai bạn có bằng nhau hay không?
b) Tính phương sai của mẫu số liệu thống kê kết quả 5 lần nhảy xa của mỗi bạn. Từ đó cho biết bạn nào có kết quả nhảy xa ổn định hơn.
Cho mẫu số liệu: 1 2 4 5 9 10 11
a) Số trung bình cộng của mẫu số liệu trên là:
A. 5.
B. 5,5.
C. 6.
D. 6,5.
b) Trung vị của mẫu số liệu trên là:
A. 5.
B. 5,5.
C. 6.
D. 6,5.
c) Tứ phân vị của mẫu số liệu trên là:
A. \({Q_1}{\rm{ }} = {\rm{ }}4,{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}5,{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}9\) .
B. \({Q_1}{\rm{ }} = {\rm{ }}1,{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}5,5,{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}11\) .
C. \({Q_1}{\rm{ }} = {\rm{ }}1,{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}5,{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}11\) .
D. \({Q_1}{\rm{ }} = {\rm{ }}2,{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}5,{Q_3} = {\rm{ }}10\) .
d) Khoảng biến thiên của mẫu số liệu trên là:
A. 5.
B. 6.
C. 10.
D. 11.
e) Khoảng tứ phân vị của mẫu số liệu trên là:
A. 7.
B. 8.
C. 9.
D. 10.
g) Phương sai của mẫu số liệu trên là:
A. \(\sqrt {\frac{{96}}{7}} \).
B. \(\frac{{96}}{7}\).
C. 96.
D. \(\sqrt {96} \).
h) Độ lệch chuẩn của mẫu số liệu trên là:
A. \(\sqrt {\frac{{96}}{7}} \)
B. \(\frac{{96}}{7}\)
C. 96
D. \(\sqrt {96} \)
Em hãy tìm hiểu chiều cao của tất cả các bạn trong tổ và lập mẫu số liệu với kết quả tăng dần. Với mẫu số liệu đó, hãy tìm:
a) Số trung bình cộng, trung vị và tứ phân vị.
b) Khoảng biến thiên và khoảng tứ phân vị.
c) Phương sai và độ lệch chuẩn.
Tỉ lệ hộ nghèo (%) của 10 tỉnh/ thành phố thuộc đồng bằng sông hồng trong năm 2010 và năm 2016 được cho trong bảng sau:
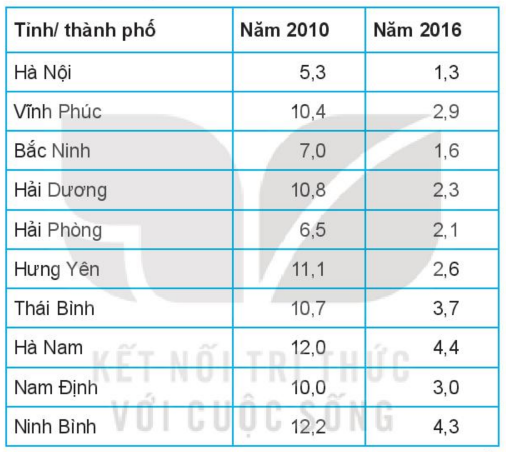
a) Tính số trung bình và độ lệch chuẩn của tỉ lệ hộ nghèo các tỉnh/ thành phố thuộc đồng bằng sông Hồng trong các năm 2010, 2016.
b) Dựa trên kết quả nhận được, em có nhận xét gì về số trung bình và độ phân tán của tỉ lệ hộ nghèo các tỉnh/ thành phố thuộc đồng bằng sông Hồng trong các năm 2010 và 2016.
Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2021, bạn Lan thu được kết quả như bảng sau:

Giả sử \({x_1};{x_2};...;{x_{40}}\) là số cuốn sách mỗi bạn trong lớp đọc được trong năm 2021 được sắp xếp theo thứ tự không giảm.
a) \({x_{13}} = 4\).
b) Mốt của mẫu số liệu là 5.
c) Số cuốn sách trung bình mỗi bạn đọc được là 5 (làm tròn đến hàng đơn vị).
d) Phương sai của mẫu số liệu trên là 2 (làm tròn đến hàng đơn vị).
Cho mẫu số liệu thống kê về sản lượng chè thu được trong một năm (kg/sào) của 10 hộ gia đình.

a) Sản lượng chè trung bình thu được trong một năm của mỗi gia đình là 113,6.
b) Khoảng biến thiên của mẫu số liệu là 5.
c) Số trung vị là 113.
d) Khoảng tứ phân vị của mẫu số liệu đã cho là 3.
Giá bán lúc 10h sáng của một mã cổ phiếu A trong 10 ngày liên tiếp được ghi lại ở biểu đồ sau (đơn vị: nghìn đồng).
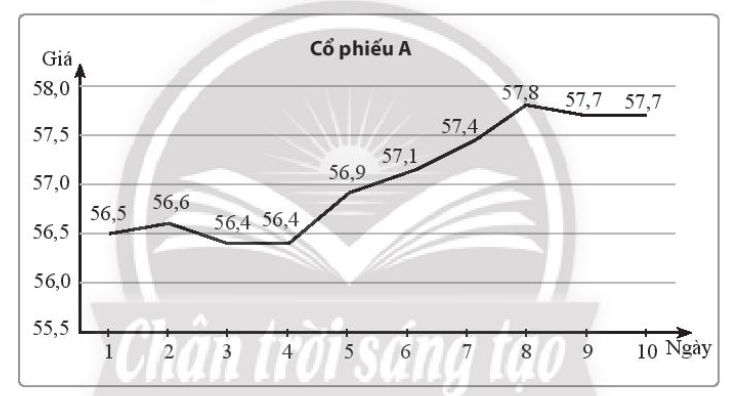
a) Viết mẫu số liệu thống kê giá của mã cổ phiếu A từ biểu đồ trên.
b) Tìm khoảng biến thiện, khoảng tứ phân vị của mẫu số liệu đó.
c) Tính trung bình, độ lệch chuẩn của mẫu số liệu trên.
Cho mẫu số liệu: 1 3 6 8 9 12
a) Số trung bình cộng của mẫu số liệu trên là:
A. 6
B. 6,5
C. 7
D. 8
b) Trung vị của mẫu số liệu trên là:
A. 6
B. 6,5
C. 7
D. 8
c) Tứ phân vị của mẫu số liệu trên là:
A. \({Q_1} = 3;{Q_2} = 6,5;{Q_3} = 9\)
B. \({Q_1} = 1;{Q_2} = 6,5;{Q_3} = 12\)
C. \({Q_1} = 6;{Q_2} = 7;{Q_3} = 8\)
D. \({Q_1} = 3;{Q_2} = 7;{Q_3} = 9\)
Tính đến ngày 19/01/2022, trong bảng xếp hạng giải bóng đá Ngoại hạng Anh (Vòng 24), số điểm của 5 đội dẫn đầu bảng như sau:
|
Đội |
Manchester City |
Liverpool |
Chelsea |
West Ham |
Arsenal |
|
Điểm |
56 |
45 |
43 |
37 |
35 |
a) Số trung bình cộng của mẫu số liệu trên là:
A. 43
B. 43,2
C. 44
D. 56
b) Trung vị của mẫu số liệu trên là:
A. 43
B. 43,2
C. 44
D. 56
c) Tứ phân vị của mẫu số liệu trên là:
A. \({Q_1} = 45;{Q_2} = 43;{Q_3} = 37\)
B. \({Q_1} = 56;{Q_2} = 43;{Q_3} = 35\)
C. \({Q_1} = 36;{Q_2} = 43;{Q_3} = 50,5\)
D. \({Q_1} = 50,5;{Q_2} = 43;{Q_3} = 36\)
Thời gian (đơn vị: phút) hoàn thành một bài kiểm tra trực tuyến của 8 học sinh lần lượt là:
40 35 45 42 44 38 43 39
Đối với mẫu số liệu trên, hãy tìm:
a) Sô trung bình cộng.
b) Trung bị.
c) Tứ phân vị.
Cho mẫu số liệu: 21 22 23 24 25.
a) Khoảng biến thiên của mẫu số liệu trên là:
A. 1
B. 2
C. 3
D. 4
b) Khoảng tứ phân vị của mẫu số liệu trên là:
A. 1
B. 2
C. 3
D. 4
c) Phương sai của mẫu số liệu trên là:
A. 1
B. 2
C. 3
D. 4
d) Độ lệch chuẩn của mẫu số liệu trên là:
A. 1
B. \(\sqrt 2 \)
C. \(\sqrt 3 \)
D. 4
Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được cho ở bảng sau:
|
Ngày |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
Nhiệt độ (độ C) |
23 |
25 |
26 |
27 |
27 |
27 |
27 |
21 |
19 |
18 |
a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên.
b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó.
Cho mẫu số liệu: 3 4 6 9 13
a) Trung vị của mẫu số liệu trên là:
A. 7
B. 6
C. 6,5
D. 8
b) Số trung bình cộng của mẫu số liệu trên là:
A. 7
B. 6
C. 6,5
D. 8
c) Khoảng biến thiên của mẫu số liệu trên là:
A. 7
B. 6
C. 1
D. 10
d) Tứ phân vị của mẫu số liệu trên là:
A. \({Q_1} = 4;{Q_2} = 6;{Q_3} = 9\)
B. \({Q_1} = 3,5;{Q_2} = 6;{Q_3} = 9\)
C. \({Q_1} = 4;{Q_2} = 6;{Q_3} = 11\)
D. \({Q_1} = 3,5;{Q_2} = 6;{Q_3} = 11\)
e) Khoảng tứ phân vị của mẫu số liệu trên là:
A. 7,5
B. 6
C. 1
D. 10
g) Phương sai của mẫu số liệu trên là:
A. 66
B. 13,2
C. \(\sqrt {66} \)
D. \(\sqrt {13,2} \)
h) Độ lệch chuẩn của mẫu số liệu trên là:
A. 66
B. 13,2
C. \(\sqrt {66} \)
D. \(\sqrt {13,2} \)
Bảng dưới đây thống kê sản lượng thủy sản của VN từ năm 2013 đến năm 2020 (đơn vị: triệu tấn).
|
Năm |
2013 |
2014 |
2015 |
2016 |
2017 |
2018 |
2019 |
2020 |
|
Sản lượng (triệu tấn) |
6,053 |
6,319 |
6,563 |
6,728 |
7,279 |
7,743 |
8,150 |
8,410 |
a) Viết mẫu số liệu thống kê sản lượng thủy sản của VN nhận đươc từ bảng trên.
b) Tìm số trung bình cộng, trung bị và tứ phân vị của mẫu số liệu đó.
c) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.
d) Tìm phương sai và độ lệch chuẩn của mẫu số liệu đó.
Bảng sau đây cho biết lượng mưa trung bình hằng tháng tại Đà Nẵng và Hà Nội (mm).
|
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đà Nẵng |
39,5 |
13,2 |
14,1 |
28,0 |
60,2 |
62,5 |
58,6 |
119,6 |
291,2 |
253,5 |
304,0 |
145,1 |
|
Hà Nội |
13,0 |
11,9 |
29,2 |
52,5 |
126,3 |
160,1 |
204,0 |
226,2 |
173,8 |
84,8 |
45,0 |
14,1 |
(Theo WWW.Weatherspark.com)
a) Đà Nẵng hay Hà Nội có lượng mưa trung bình cả năm cao hơn?
b) Tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của hai mẫu số liệu về lượng mưa trung bình các tháng tại Đà Nẵng và Hà Nội. Nhận xét gì về sự phân tán của hai mẫu số liệu này?
Nhiệt độ trung bình các tháng trong một năm gần đây của tỉnh Bắc Ninh được cho bởi bảng thống kê bên dưới (đơn vị: độ C, nguồn: https://vi.weatherspark.com/):
17, 18, 21, 24, 27, 29, 29, 28, 25, 22, 18.
a) Một của mẫu số liệu trên là 29.
b) Khoảng biến thiên của mẫu số liệu trên là 9.
c) Số trung bình của mẫu số liệu đã cho bằng 23,92.
d) Số trung vị của mẫu số liệu đã là 24,5.







Danh sách bình luận