Tung một đồng xu hai lần liên tiếp. Tính xác suất của biến cố “Kết quả của hai lần tung là khác nhau”.
+) Bước 1: Tính số phần tử của không gian mẫu “\(n\left( \Omega \right)\)” và số phần tử của kết quả có lợi cho biến cố “\(n\left( A \right)\)”
+) Bước 2: Xác suất của biến cố là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)
+) Không gian mẫu trong trò chơi trên là tập hợp \(\Omega = {\rm{ }}\left\{ {SS;{\rm{ }}SN;{\rm{ }}NS;{\rm{ }}NN} \right\}\). Vậy \(n\left( \Omega \right) = 4\)
+) Gọi A là biến cố “Kết quả của hai lần tung là khác nhau”.
Các kết quả thuận lợi cho biến cố A là: \(SN;{\rm{ }}NS\) tức là \(A = \left\{ {SN;NS} \right\}\).Vậy \(n\left( A \right) = 2\)
+) Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{2}{4} = \frac{1}{2}\)

Các bài tập cùng chuyên đề
Tung một đồng xu hai lần liên tiếp. Xét biến cố “Có ít nhất một lần xuất hiện mặt sấp”. Tính xác suất của biến cố nói trên.
Viết tỉ số giữa số phần tử của tập hợp A và số phần tử của tập hợp \(\Omega \).
Gieo một xúc xắc hai lần liên tiếp. Xét biến cố “Số chấm trong hai lần gieo đều là số nguyên tố”. Tính xác suất của biến cố đó.
Viết tỉ số giữa số phần tử của tập hợp C và số phần tử của tập hợp \(\Omega\).
Tung một đồng xu ba lần liên tiếp.
a) Viết tập hợp \(\Omega \) là không gian mẫu trong trò chơi trên.
b) Xác định mỗi biến cố:
A: “Lần đầu xuất hiện mặt ngửa”.
B: “Mặt ngửa xảy ra đúng một lần”.
Gieo một xúc xắc hai lần liên tiếp. Tính xác suất của mỗi biến cố sau:
a) “Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10”.
b) “Mặt 1 chấm xuất hiện ít nhất một lần”.
Có 5 bông hoa màu trắng, 5 bông hoa màu vàng và 6 bông hoa màu đỏ. Người ta chọn ra 4 bông hoa từ các bông hoa trên. Tính xác suất của biến cố “Bốn bông hoa chọn ra có cả ba màu”.
Xét phép thử “Tung một đồng xu hai lần liên tiếp”. Tính xác suất của biến cố A: “Mặt xuất hiện của đồng xu ở cả hai lần tung là giống nhau”.
Xét phép thử T: “Tung một đồng xu hai lần liên tiếp”. Không gian mẫu của phép thử trên là tập hợp \(\Omega {\rm{ }} = {\rm{ }}\left\{ {SS;{\rm{ }}SN;{\rm{ }}NS;{\rm{ }}NN} \right\}.\)
a) Sự kiện “Kết quả của hai lần tung là giống nhau” tương ứng với tập con A nào của tập hợp \(\Omega \)?
b) Phát biểu tập con \(B{\rm{ }} = {\rm{ }}\left\{ {SN;{\rm{ }}NS} \right\}\) của không gian mẫu \(\Omega \) dưới dạng mệnh đề nêu sự kiện.
Giao một xúc xắc hai lần liên tiếp. Xét biến cố "Có ít nhất một lần xuất hiện mặt 6 chấm". Làm thế nào để tính được xác suất biến cố nói trên?
Có 15 bông hoa màu trắng và 15 bông hoa màu vàng. Người ta chọn ra đồng thời 10 bông hoa. Tính xác suất của biến cố “Trong 10 bông hoa được chọn ra có ít nhất một bông màu trắng”.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên đồng thời 2 chiếc thẻ từ trong hộp.
a) Gọi \(\Omega \) là không gian mẫu trong trò chơi trên. Tính số phần tử của tập hợp \(\Omega \).
b) Tính xác suất của biến cố “Tích các số trên hai thẻ là số lẻ”.
Một hộp có 4 tấm bìa cùng loại, mỗi tấm bìa được ghi một trong các số 1, 2, 3, 4 hai tấm bìa khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên đồng thời 3 tấm bìa từ trong hộp.
a) Tính số phần tử của không gian mẫu.
b) Xác định các biến cố sau:
A: “Tổng các số trên ba tấm bìa bằng 9”.
B: “Các số trên ba tấm bìa là ba số tự nhiên liên tiếp”.
c) Tính P(A), P(B).
Hai bạn nữ Hoa, Thảo và hai bạn nam Dũng, Huy được xếp ngồi ngẫu nhiên vào bốn ghế đặt theo hàng dọc. Tính xác suất của mỗi biến cố:
a) “Bạn Thảo ngồi ghế đầu tiên”.
b) “Bạn Thảo ngồi ghế đầu tiên và bạn Huy ngồi ghế cuối cùng”.
Có 10 bông hoa màu trắng, 10 bông hoa màu vàng và 10 bông hoa màu đỏ. Người ta chọn ra 4 bông hoa từ các bông hoa trên. Tính xác suất của biến cố “Bốn bông hoa chọn ra có cả ba màu”.
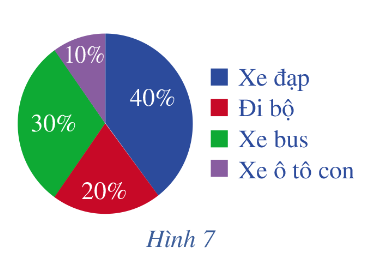
Lớp 10A có 40 học sinh. Tỉ số phần trăm về phương tiện mà các bạn đến trường được mô tả như biểu đồ ở Hình 7.
a) Có bao nhiêu bạn đi xe đạp đến trường?
b) Chọn ngẫu nhiên một bạn để phân công vào đội xung kích của trường. Tính xác suất của biến cố “Bạn được chọn là bạn đến trường bằng xe đạp”.
Trong một hội thảo quốc tế có 10 chuyên gia đến từ các nước ở châu Á, 12 chuyên gia đến từ các nước ở châu Âu. Chọn ngẫu nhiên 2 chuyên gia vào ban tổ chức. Xác suất của biến cố “Chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức” bằng bao nhiêu?
Trong một buổi khiêu vũ có đúng 10 cặp vợ chồng. Chọn ngẫu nhiên 2 người lên khiêu vũ đầu tiên. Xác suất của biến cố “Chọn được 2 người là vợ chồng” bằng bao nhiêu?
Một lô hàng có 20 sản phẩm bao gồm 16 chính phẩm và 4 phế phẩm. Chọn ngẫu nhiên 3 sản phẩm.
a) Có bao nhiêu kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm?
b) Xác suất của biến cố “Cả 3 sản phẩm được chọn là chính phẩm” bằng bao nhiêu?
Trong một hộp có 20 chiếc thẻ cùng loại được viết các số 1, 2, 3, ..., 20 sao cho mỗi thẻ chỉ viết một số và hai thẻ khác nhau viết hai số khác nhau. Chọn ngẫu nhiên 2 chiếc thẻ. Tính xác suất của biến cố “Hai thẻ được chọn có tích của hai số được viết trên đó là số lẻ”.
Gieo một con xúc xắc. Gọi K là biến cố: “Số chấm xuất hiện trên con xúc xắc là một số nguyên tố".
a) Biến cố: “Số chấm xuất hiện trên con xúc xắc là một hợp số" có là biến cố K không?
b) Biến cố K và K là tập con nào của không gian mẫu?
Một hộp chứa 12 tấm thẻ được đánh số 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Rút ngẫu nhiên từ hộp đó một tấm thẻ.
a) Mô tả không gian mẫu \(\Omega \). Các kết quả có thể có đồng khả năng không?
b) Xét biến cố E: “Rút được thẻ ghi số nguyên tố". Biến cố E là tập con nào của không gian mẫu?
c) Phép thử có bao nhiêu kết quả có thể? Biến cố E có bao nhiêu kết quả thuận lợi? Từ đó, hãy tính xác suất của biến cố E.
Chọn ngẫu nhiên một số nguyên dương không lớn hơn 30.
a) Mô tả không gian mẫu.
b) Gọi A là biến cố: “Số được chọn là số nguyên tố". Các biến cố A và \(\overline A \) là tập con nào của không gian mẫu?
Chọn ngẫu nhiên một số nguyên dương không lớn hơn 22.
a) Mô tả không gian mẫu.
b) Gọi B là biến cố: “Số được chọn chia hết cho 3". Các biến cố B và \(\overline B \) là các tập con nào của không gian mẫu?
Theo định nghĩa cổ điển của xác suất, để tính xác suất của biến cố F: “Bạn An trúng giải độc đắc" và biến cố G: “Bạn An trúng giải nhất" ta cần xác định n(\(\Omega \) ), n(F) và n(G). Liệu có thể tính n(\(\Omega \)), n(F) và n(G) bằng cách liệt kê ra hết các phần tử của \(\Omega \), F và G rồi kiểm đếm được không?
Màu hạt của đậu Hà Lan có hai kiểu hình là màu vàng và màu xanh tương ứng với hai loại gen là gen trội A và gen lặn a. Hình dạng hạt của đậu Hà Lan có hai kiểu hình là hạt trơn và hạt nhân tương ứng với hai loại gen là gen trội B và gen lặn b. Biết rằng, cây Con lấy ngẫu nhiên một gen từ cây bố và một gen từ cây mẹ. Phép thử là cho lai hai loại đậu Hà Lan, trong đó cả cây bố và cây mẹ đều có kiểu gen là (Aa, Bb) và kiểu hình là hạt màu vàng và trơn. Giả sử các kết quả có thể là đồng khả năng. Tính xác suất để cây con cũng có kiểu hình là hạt màu vàng và trơn.
Trong ví dụ 4, hãy xác định các kết quả thuận lợi cho biến cố:
a) “Trong ba bạn được chọn có đúng một bạn nữ”.
b) “Trong ba bạn được chọn không có bạn nam nào”.
Ví dụ 4: Một nhóm có 5 bạn nam và 4 bạn nữ. Chọn ngẫu nhiên cùng một lúc ra 3 bạn đi làm công tác tình nguyện.
Chọn ngẫu nhiên một số nguyên dương nhỏ hơn 100.
a) Hãy mô tả không gian mẫu.
b) Gọi A là biến cố “Số được chọn là số chính phương”. Hãy viết tập hợp mô tả biến cố A.
c) Gọi B là biến cố “Số được chọn chia hết cho 4” Hãy tính số các kết quả thuận lợi cho B.
Gieo hai con xúc xắc. Hãy tính số kết quả thuận lợi cho biến cố:
a) “Số chấm xuất hiện trên hai con xúc xắc hơn kém nhau 3 chấm”.
b) “Tích số chấm xuất hiện trên hai con xúc xắc chia hết cho 5”.
c) “Tổng số chấm xuất hiện trên hai con xúc xắc là số lẻ”.
Xếp 4 viên bi xanh và 5 viên bi trắng có các kích thước khác nhau thành một hàng ngang một cách ngẫu nhiên. Hãy tính số các kết quả thuận lợi cho biến cố:
a) “Không có hai viên bi trắng nào xếp liền nhau”.
b) “Bốn viên bi xanh được xếp liền nhau”.







Danh sách bình luận