Hãy nhắc lại công thức tính khoảng cách giữa 2 điểm \(I\left( {a;b} \right)\) và \(M\left( {x;y} \right)\) trong mặt phẳng Oxy.
Khoảng cách hai điểm M, I (hay độ dài đoạn thẳng MI) chính là độ dài vecto \(\overrightarrow {MI} \)
\(\overrightarrow {MI} = \left( {a - x;b - y} \right) \Rightarrow \left| {\overrightarrow {MI} } \right| = \sqrt {{{\left( {a - x} \right)}^2} + {{\left( {;b - y} \right)}^2}} \)
Vậy khoảng cách giữa hai điểm \(I\left( {a;b} \right)\) và \(M\left( {x;y} \right)\) là \(\sqrt {{{\left( {a - x} \right)}^2} + {{\left( {;b - y} \right)}^2}} \)
Các bài tập cùng chuyên đề
Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)đều khác \(\overrightarrow 0 \). Những khẳng định nào sau đây là đúng?
a) \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đều cùng hướng với vectơ \(\overrightarrow 0 \);
b) Nếu \(\overrightarrow b \)không cùng hướng với \(\overrightarrow a \) thì \(\overrightarrow b \) ngược hướng với \(\overrightarrow a \).
c) Nếu \(\overrightarrow a \) và \(\overrightarrow b \) đều cùng phương với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương.
d) Nếu \(\overrightarrow a \) và \(\overrightarrow b \) đều cùng hướng với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng hướng.
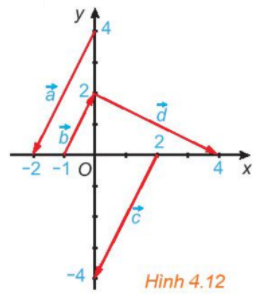
Trong Hình 4.12, hãy chỉ ra các vecto cùng phương, các cặp vecto ngược hướng và các cặp vecto bằng nhau.
Trên mặt phẳng tọa độ Oxy hãy vẽ các vecto \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) với A (1; 2), M (0; -1), N (3; 5).
a) Chỉ ra mỗi quan hệ giữa hai vecto trên.
b) Một vật thể khởi hành từ M chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn vởi vecto \(\overrightarrow v = \overrightarrow {OA} \). Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu sẽ tới N?
Cho đoạn thẳng MN có trung điểm là I.
a) Viết các vectơ khác vectơ-không có điểm đầu, điểm cuối là một trong ba điểm M, N, I.
b) vectơ nào bằng \(\overrightarrow {MI} \)? Bằng \(\overrightarrow {NI} \)?
Cho hình thang ABCD có hai đáy là AB và CD. Tìm vectơ:
a) Cùng hướng với \(\overrightarrow {AB} \)
b) Ngược hướng với \(\overrightarrow {AB} \)
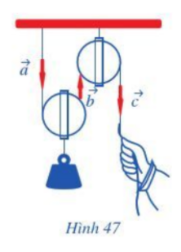
Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)(Hình 47).
a) Hãy chỉ ra các cặp vectơ cùng phương.
b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.
Hãy chỉ ra các cặp vectơ cùng hướng, ngược hướng, bằng nhau trong hình 17.
Gọi O là tâm hình lục giác đều ABCDEF.
a) Tìm các vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \).
b) Tìm các vectơ bằng vectơ \(\overrightarrow {AB} \).
Cho trước hai vectơ không cùng hướng \(\overrightarrow a \) và \(\overrightarrow b \). Hỏi có hay không một vectơ cùng phương với cả \(\overrightarrow a \) và \(\overrightarrow b \)?
Cho ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) cùng phương và cùng khác vectơ \(\overrightarrow 0 \). Chứng minh rằng có ít nhất hai vectơ trong chúng có cùng hướng.
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Xét các vectơ có hai điểm mút lấy từ các điểm \(O,\,\,A,\,\,B,\,\,C,\,\,D,\,\,E,\,\,F\).
a) Hãy chỉ ra các vectơ khác vectơ – không và cùng phương với vectơ \(\overrightarrow {OA} \).
b) Tìm các vectơ bằng vectơ \(\overrightarrow {AB} \).
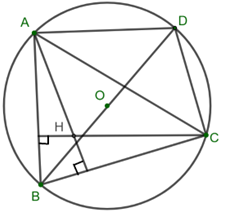
Cho tam giác \(ABC\) không vuông, với trực tâm \(H\), nội tiếp đường tròn \((O).\) Kẻ đường kính \(AA'\) của đường tròn \((O).\)
a) Chứng minh rằng \(\overrightarrow {BH} = \overrightarrow {A'C} .\)
b) Gọi \(M\) là trung điểm của \(BC.\) Tìm mối quan hệ về phương, hướng và độ dài của hai vectơ \(\overrightarrow {AH} \) và \(\overrightarrow {OM} .\)
Cho hình thoi \(ABCD\) có độ dài các cạnh bằng 1 và \(\widehat {DAB} = {120^ \circ }.\) Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AB} = \overrightarrow {CD} \)
B. \(\overrightarrow {BD} = \overrightarrow {AC} \)
C. \(\left| {\overrightarrow {BD} } \right| = 1\)
D. \(\left| {\overrightarrow {AC} } \right| = 1\)
Cho hình thang ABCD có AB và CD song song với nhau. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {AB} = \overrightarrow {CD} \)
B. \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
C. \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
D. \(\overrightarrow {AB} = \overrightarrow {DC} \)
Cho hình vuông ABCD có cạnh bằng a. Tính \(\left| {\overrightarrow {AB} } \right|,\left| {\overrightarrow {AC} } \right|\).
Cho đường tròn tâm O và dây cung BC không đi qua O. Điểm A chuyển động trên cung lớn BC của đường tròn sao cho tam giác ABC nhọn. Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\overrightarrow {AH} \) có độ dài không đổi.
Cho hình chữ nhật ABCD có tâm O là giao điểm của hai đường chéo. Hãy chi ra một cặp vectơ
a) Cùng hướng
b) Ngược hướng
c) Bằng nhau
Cho hình chữ nhật ABCD có \(AB = 3,BC = 4\). Độ dài của vectơ \(\overrightarrow {AC} \) là:
A. 5
B. 6
C. 7
D. 9
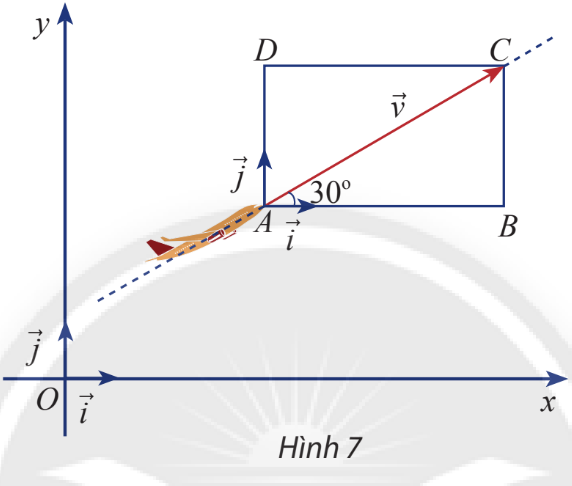
Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc \(30^\circ \) (hình 7).
a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD.
b) Biểu diễn vận tốc \(\overrightarrow v \) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \).
c) Tìm tọa độ của \(\overrightarrow v \).
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\).
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy.
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị \(\overrightarrow i \) và \(\overrightarrow j \) lần lượt trên hai trục tọa độ Ox và Oy.
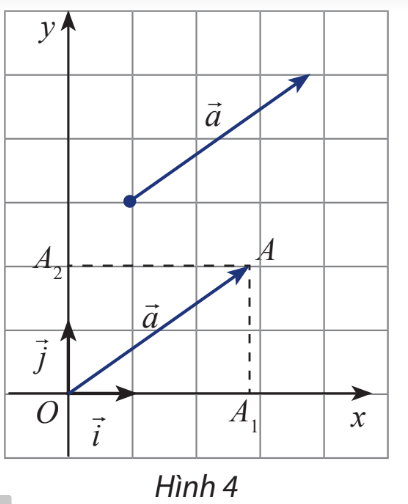
Trong mặt phẳng Oxy, cho một vectơ \(\overrightarrow a \)tùy ý. Vẽ \(\overrightarrow {OA} = \overrightarrow a \)và gọi \({A_1},{A_2}\)lần lượt là hình chiếu vuông góc của A lên Ox và Oy (hình 4). Đặt \({\overrightarrow {OA} _1} = x\overrightarrow i \), \({\overrightarrow {OA} _2} = y\overrightarrow j \). Biểu diễn vectơ \(\overrightarrow a \)theo hai vectơ và \(\overrightarrow j \).
Nêu nhận xét về độ lớn, phương và chiều của vectơ trên trục \(Ox\) và vectơ \(\overrightarrow j \) trên trục \(Oy\) (hình 1).
Chứng minh rằng:
a) \(\overrightarrow a = \left( {4; - 6} \right)\) và \(\overrightarrow b = \left( { - 2;3} \right)\) là hai vectơ ngược hướng.
b) \(\overrightarrow a = \left( { - 2;3} \right)\) và \(\overrightarrow b = \left( { - 8;12} \right)\) là hai vectơ cùng hướng.
c) \(\overrightarrow a = \left( {0;4} \right)\) và \(\overrightarrow b = \left( {0; - 4} \right)\) là hai vectơ đối nhau.
