Xét một elip (E) với các kí hiệu như trong định nghĩa. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm của \({F_1}{F_2}\) , tia Ox trùng tia\(O{F_2}\)(H721).

a) Nêu toạ độ của các tiêu điểm \({F_1},{F_2}\).

b) Giải thích vì sao điểm M(x;y) thuộc elip khi và chỉ khi \(\sqrt {{{\left( {x + c} \right)}^2} + {y^2}}  + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}}  = 2a\).

Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\). Tìm các tiêu điểm và tiêu cự của elip.

Trên bàn bida hình elip có một lỗ thu bị tại một tiêu điểm (H.7.20). Nếu gậy chơi tác động đủ mạnh vào một bị đặt tại tiêu điểm còn lại của bạn, thì sau khi va vào thành bàn, bị sẽ bật lại và chạy về lỗ thu (bỏ qua các tác động phụ). Hỏi độ dài quãng đường bi lăn từ điểm xuất phát tới lỗ thu có phụ thuộc vào đường đi của bị hay không? Vì sao?

Tại sao trong định nghĩa elip cần điều kiện a > c?

Cho Elip có phương trình \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\). Tìm tiêu điểm và tiêu cự của elip.

Lập phương trình chính tắc của elip đi qua hai điểm \(A\left( {5;0} \right)\) và có một tiêu điểm là \({F_2}\left( {3;0} \right)\).

Phương trình nào sau đây là phương trình chính tắc của đường elip?

A. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{9} = 1\)

B. \(\frac{{{x^2}}}{1} + \frac{{{y^2}}}{6} = 1\)

C. \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{1} = 1\)

D. \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} = 1\)

Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\)

a) Tìm các giao điểm \({A_1},{A_2}\)  của (E) với trục hoành và các giao điểm \({B_1},{B_2}\) của (E) với trục tung. Tính \({A_1}{A_2},{B_1}{B_2}\).

b) Xét một điểm bất kì \(M\left( {{x_o};{y_o}} \right)\) thuộc (E).

Chứng minh rằng, \({b^2} \le x_o^2 + y_o^2 \le {a^2}\) và \(b \le OM \le a\).

Chú ý: \({A_1}{A_2},{B_1}{B_2}\)tương ứng được gọi là trục lớn, trục nhỏ của elip (E) và tương ứng có độ dài là 2a, 2b.

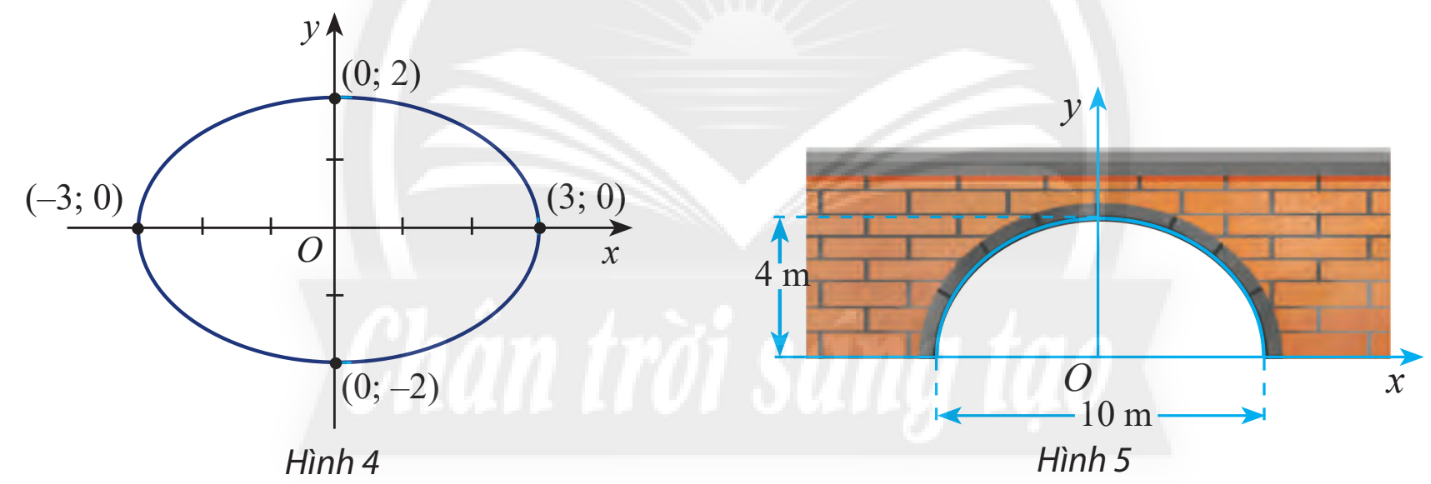
Một đường hầm có mặt các hình nửa Elip cao 4 m, rộng 10 m (hình 5). Viết phương trình chính tắc của elip đó.

Viết phương trình chính tắc của elip trong hình 4.

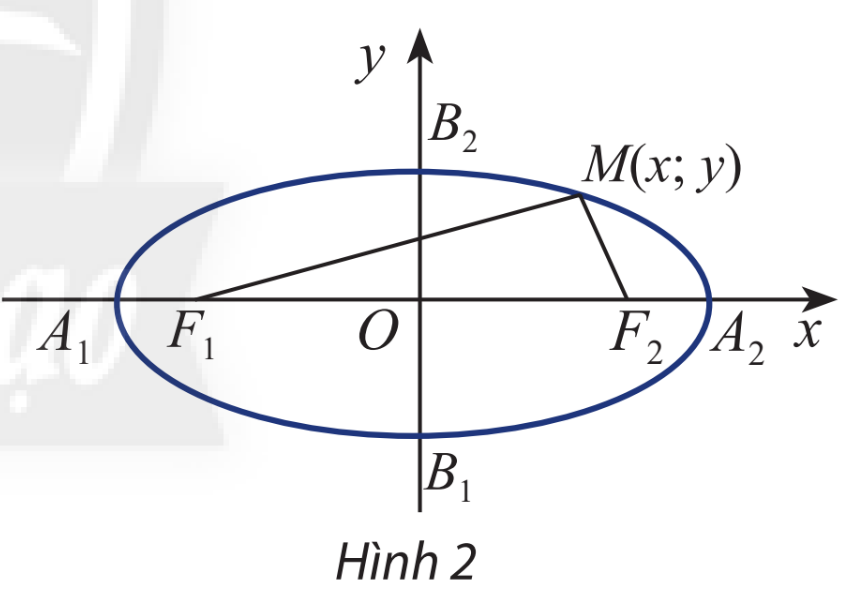
Cho elip (E) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\)

Xét điểm \(M(x;y)\)

a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c.

b) Giải thích phát biểu sau:

\(M(x;y) \in (E) \Leftrightarrow \sqrt {{{\left( {x + c} \right)}^2} + {y^2}}  + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}}  = 2a\).

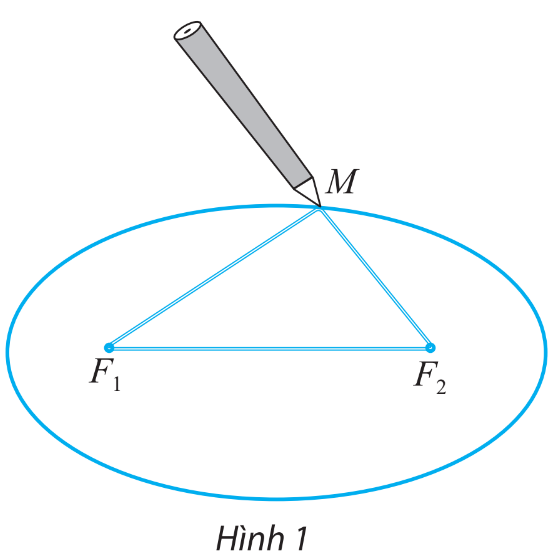
Lấy một tấm bìa, ghim hai cái đinh lên đó tại hai điểm \({F_1}\) và \({F_2}\). Lấy một vòng dây kín không đàn hồi  có độ dài lớn hơn hai lần đoạn \({F_1}{F_2}\). Quàng vòng dây đó qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường mà người ta gọi là đường elip.

Cho biết 2c là khoảng cách \({F_1}{F_2}\) và \(2a + 2c\) là độ dài của vòng dây.

Tính tổng hai khoảng cách \({F_1}M\) và \({F_2}M\).

Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ của các elip sau:

a) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)

b) \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)

c) \({x^2} + 16{y^2} = 16\)

Viết phương trình chính tắc của elip thỏa mãn từng điều kiện:

a) Đỉnh \((5;0),(0;4)\)

b) Đỉnh \((5;0)\), tiêu điểm \((3;0)\)

c) Độ dài trục lớn 16, độ dài trục nhỏ 12

d) Độ dài trục lớn 20, tiêu cự 12

Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M sao cho \(M{F_1} + M{F_2} = 2a\), ở đó \({F_1}{F_2} = {\rm{ }}2c\) (với a > c > 0). Ta chọn hệ trục toạ độ Oxy có gốc là trung điểm của \({F_1}{F_2}\), trục Oy là đường trung trực của \({F_1}{F_2}\), và \({F_2}\) nằm trên tia Ox (Hình 52). Khi đó, \({F_1}\left( { - c;0} \right)\) và \({F_2}\left( {c;0} \right)\) là hai tiêu điểm của elip (E). Chứng minh rằng:

a) \({A_1}\left( { - a;0} \right)\) và \({A_2}\left( {a{\rm{ }};{\rm{ }}0} \right)\) đều là giao điểm của elip (E) với trục Ox.

b) \({B_1}\left( {0; - {\rm{ }}b} \right)\) và\({B_2}\left( {0;{\rm{ }}b} \right)\) , ở đó\(b = \sqrt {{a^2} - {c^2}} \), đều là giao điểm của elip (E) với trục Oy.

Lập phương trình chính tắc của elip (E) đi qua hai điểm M(0 ; 3) và \(N\left( {3; - \frac{{12}}{5}} \right)\).

Phương trình nào sau đây là phương trình chính tắc của elip?

a) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{64}} = 1\)

b) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{64}} = 1\)

c) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\)

d) \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{64}} = 1\)

Cho elip \(\left( E \right)\) có phương trình chính tắc \(\frac{{{x^2}}}{{49}} + \frac{{{y^2}}}{{25}} = 1\) .Tìm tọa độ các giao điểm của \(\left( E \right)\) với trục Ox, Oy và tọa độ các tiêu điểm của \(\left( E \right)\).

Viết phương trình chính tắc của elip \(\left( E \right)\), biết tọa độ hai giao điểm của \(\left( E \right)\) với Ox và Oy lần lượt là \({A_1}\left( { - 5;0} \right)\) và \({B_2}\left( {0;\sqrt {10} } \right)\).

Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có \({A_1}{A_2}\) = 768 800 km và \({B_1}{B_2}{\rm{ }} = {\rm{ }}767{\rm{ }}619{\rm{ }}km\) (Nguồn: Ron Larson (2014), Precalculus Real Mathematics, Real People, Cengage) (Hình 62). Viết phương trình chính tắc của elip đó.

Cho elip \(\left( E \right)\) có phương trình \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\). Tìm tiêu điểm và tiêu cự của elip.

Viết phương trình chính tắc của elip \(\left( E \right)\), biết \(\left( E \right)\) đi qua điểm \(A\left( {6;0} \right)\) và có tiêu cực bằng 8.

Cho điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc elip \(\left( E \right)\) có phương trình \(\frac{{{x^2}}}{2} + \frac{{{y^2}}}{1} = 1\).

a) Tính \(M{F_1}^2 - M{F_2}^2\) theo \({x_0};{y_0}\). Từ đó tính \(M{F_1}^2 - M{F_2}^2\) theo \({x_0};{y_0}\).

b) Tìm điểm M sao cho \(M{F_2} = 2M{F_1}\).

c) Tìm M sao cho góc nhìn của M tới hai điểm \({F_1},{F_2}\) (tức là góc \(\widehat {{F_1}M{F_2}}\)) là lớn nhất?

Cho elip \(\left( E \right)\) có phương trình \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1\). Điểm nào sau đây là một tiêu điểm của \(\left( E \right)\)?

A. \(\left( {0;3} \right)\) 

B. \(\left( {4;0} \right)\) 

C. \(\left( {3;0} \right)\) 

D. \(\left( {0;4} \right)\)

Phương trình chính tắc của elip \(\left( E \right)\) đi qua điểm \(M\left( {8;0} \right)\) và có tiêu cự bằng 6 là:

A. \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{100}} = 1\) 

B. \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{28}} = 1\)

C. \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{73}} = 1\)   

D. \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{55}} = 1\)

Phương trình chính tắc của elip có hai đỉnh là \(\left( { - 3;0} \right),\left( {3;0} \right)\) và hai tiêu điểm là \(\left( { - 1;0} \right),\left( {1;0} \right)\) là:

A. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{1} = 1\)   

B. \(\frac{{{x^2}}}{8} + \frac{{{y^2}}}{9} = 1\) 

C. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{8} = 1\)   

D. \(\frac{{{x^2}}}{1} + \frac{{{y^2}}}{9} = 1\)

Elip với độ dài hai trục là 20 và 12 có phương trình chính tắc là:

A. \(\frac{{{x^2}}}{{40}} + \frac{{{y^2}}}{{12}} = 1\)   

B. \(\frac{{{x^2}}}{{1600}} + \frac{{{y^2}}}{{144}} = 1\)     

C. \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\) 

D. \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{36}} = 1\)

Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ các elip sau:

a) \(\frac{{{x^2}}}{{169}} + \frac{{{y^2}}}{{25}} = 1\).

b) \({x^2} + 4{y^2} = 1\).

Viết phương trình chính tắc của elip thỏa mãn các điều kiện sau:

a) Độ dài trục lớn 26, độ dài trục nhỏ 10.

b) Độ dài trục lớn 10, tiêu cự 6.

Cho biết Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo Elip (E) với Trái Đất là 1 tiêu điểm. Cho biết độ dài hai trục của \(\left( E \right)\) là 768 800 km và 767 619 km. Viết phương trình chính tắc của elip (E).

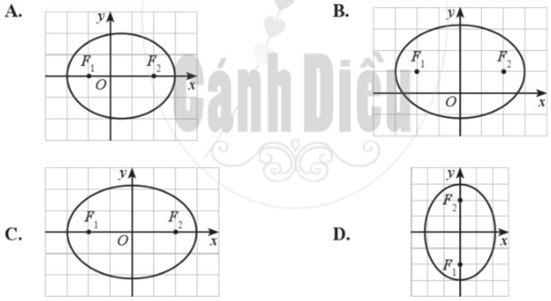
Elip trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng:
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0)?