Chứng minh rằng, đường thẳng đi qua hai điểm \(A\left( {a;0} \right),B\left( {0;b} \right)\left( {ab \ne 0} \right)\) có phương trình \(\frac{x}{a} + \frac{y}{b} = 1\).
Viết phương trình tổng quát của AB rồi biến đổi phương trình về dạng cần chứng minh.
Đường thẳng AB có một vectơ chỉ phương là \(\overrightarrow {{u_{AB}}} = \overrightarrow {AB} = \left( { - a;b} \right)\). Do đó \(\overrightarrow {{n_{AB}}} = \left( {b;a} \right)\)
Phương trình tổng quát của đường thẳng AB có vectơ pháp tuyến \(\overrightarrow {{n_{AB}}} = \left( {b;a} \right)\) và đi qua điểm \(A\left( {a;0} \right)\)là: \(b\left( {x - a} \right) + a\left( {y - 0} \right) \Leftrightarrow bx + ay - ab = 0 \Leftrightarrow \frac{x}{a} + \frac{y}{b} = 1\).

Các bài tập cùng chuyên đề
Trong mặt phẳng tọa độ, cho tam giác có ba đỉnh A(1; 3), B(-1;- 1), C(5 - 3). Lập phương trình tổng quát của đường cao kẻ từ A của tam giác ABC.
Trong mặt phẳng tọa độ, cho đường thẳng \(\Delta \) đi qua điểm \(A\left( {{x_o};{y_o}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n {\rm{ }} = \left( {a;{\rm{ }}b} \right)\). Chứng minh rằng điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \) khi và chỉ khi:
\(a\left( {x - {x_o}} \right) + b\left( {y - {y_o}} \right) = 0\).
Lập phương trình tổng quát của các trục tọa độ.
Phương trình nào sau đây là phương trình tổng quát của đường thẳng?
A. \( - x - 2y + 3 = 0\)
B. \(\left\{ \begin{array}{l}x = 2 + t\\y = 3 - t\end{array} \right.\)
C. \({y^2} = 2x\)
D. \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{6} = 1\)
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), chứng tỏ rằng điểm \(M\left( {x;y} \right)\) có tọa độ thỏa mãn phương trình: \(ax + by + c = 0\) (với \(c = - a{x_0} - b{y_0}\))
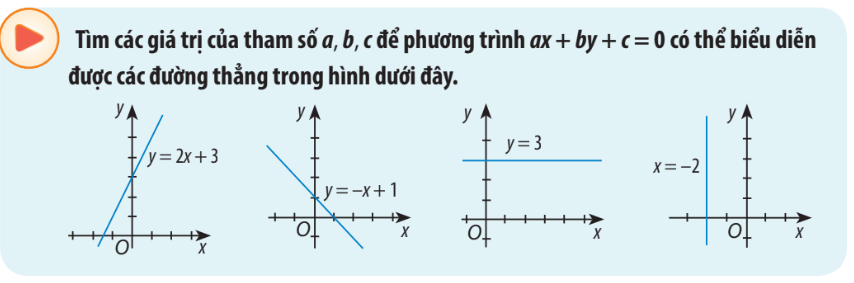
Tìm các giá trị của tham số a, b, c để phương trình ax + by + c = 0 có thể biểu diễn được các đường thẳng trong hình dưới đây.
Cho đường thẳng \(\Delta \) có phương trình tổng quát là: \(x{\rm{ }}-{\rm{ }}y{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0\) .
a) Chỉ ra toạ độ của một vectơ pháp tuyến và một vectơ chỉ phương của \(\Delta \).
b) Chỉ ra toạ độ của hai điểm thuộc \(\Delta \).
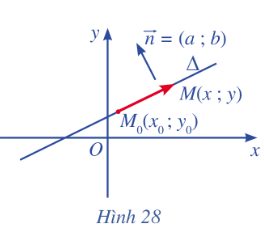
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n {\rm{ }} = \left( {a;{\rm{ }}b} \right)\). Xét điểm M(x ; y) nằm trên \(\Delta \) (Hình 28).
a) Nhận xét về phương của hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \).
b) Tìm mối liên hệ giữa toạ độ của điểm M với toạ độ của điểm \({M_o}\) và toạ độ của vectơ pháp tuyến \(\overrightarrow n \).
Lập phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm A(-1; 2) và:
a) Có vectơ pháp tuyến là \(\overrightarrow n = \left( {3{\rm{ }};{\rm{ }}2} \right).\)
b) Có vectơ chỉ phương là \(\overrightarrow u = \left( { - 2{\rm{ }};{\rm{ 3}}} \right).\)
Cho tam giác ABC, biết A(1; 3), B(-1;- 1), C(5 - 3). Lập phương trình tổng quát của:
a) Ba đường thẳng AB, BC, AC;
b) Đường trung trực cạnh AB;
c) Đường cao AH và đường trung tuyến AM của tam giác ABC.
Cho đường thẳng ∆: 2x − 3y + 5 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của ∆?
A. \(\overrightarrow {{n_1}} = (2; - 3)\)
B. \(\overrightarrow {{n_2}} = ( - 3;2)\)
C. \(\overrightarrow {{n_3}} = (2;3)\)
D. \(\overrightarrow {{n_4}} = (3;2)\)
A. \({y^2} = 3x\).
B. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\).
C. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 - 2t}\\{y = 1 + 3t{\rm{ }}}\end{array}} \right.\).
D. \(2x - y - 1 = 0\).







Danh sách bình luận