Quan sát Hình 6.2 và cho biết những điểm nào sau đây nằm trên đồ thị của hàm số \(y = \frac{1}{2}{x^2}\).
(0; 0), (2; 2), (-2; 2), (1; 2), (-1; 2).
Nêu nhận xét về mối quan hệ giữa hoành độ và tung độ của những điểm nằm trên đồ thị.
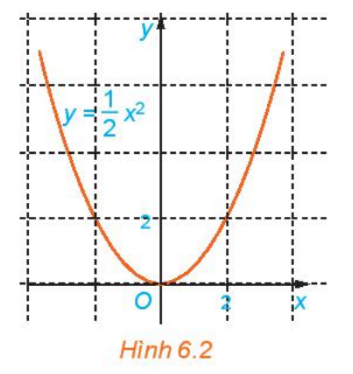
Dựa vào độ thị ta thấy (0; 0); (2; 2); (-2; 2) nằm trên đồ thị hàm số \(y = \frac{1}{2}{x^2}\).
Ta nhận ra được: \(\begin{array}{l}0 = \frac{1}{2}{.0^2}\\2 = \frac{1}{2}{.2^2}\\2 = \frac{1}{2}.{( - 2)^2}\end{array}\) Vì vậy những điểm có tọa độ \(\left( {x;\frac{1}{2}{x^2}} \right)\) sẽ nằm trên đồ thị.

Các bài tập cùng chuyên đề
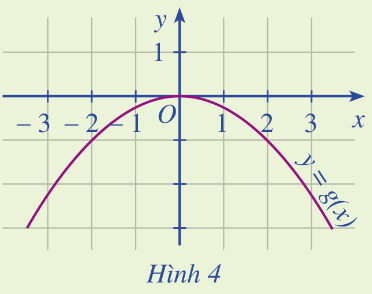
Dựa vào Hình 4, xác định \(g\left( { - 2} \right),g\left( 0 \right),g\left( 2 \right)\).
Cho hàm số \(y = \frac{1}{x}\) và ba điểm \(M\left( { - 1; - 1} \right),N\left( {0;2} \right),P\left( {2;1} \right)\). Điểm nào thuộc đồ thị hàm số trên? Điểm nào không thuộc đồ thị hàm số trên?
Xét hàm số \(y = f\left( x \right) = {x^2}\)
a) Tính các giá trị \({y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)\) tương ứng với giá trị \({x_1} = - 1;{x_2} = 1\).
b) Biểu diễn trong mặt phẳng tọa độ Oxy các điểm \({M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)\).
Cho đồ thị hàm số \(y = f\left( x \right)\) như Hình 8.
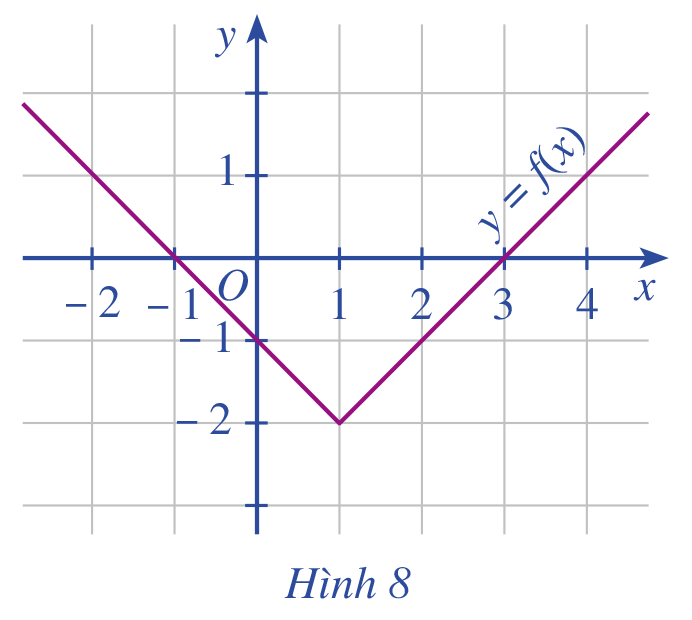
a) Trong các điểm có tọa độ \(\left( {1; - 2} \right),\left( {0;0} \right),\left( {2; - 1} \right)\), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số?
b) Xác định \(f\left( 0 \right);f\left( 3 \right)\).
c) Tìm điểm thuộc đồ thị có tung độ bằng 0.
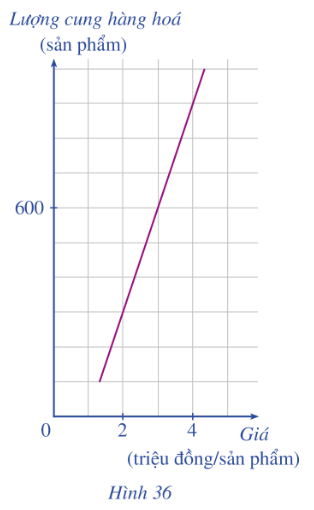
Đồ thị ở Hình 36 cho thấy sự phụ thuộc của lượng hàng hoá được sản xuất (cung) (đơn vị; sản phẩm) bởi giá bán (đơn vị: triệu đồng/sản phẩm) đối với một loại hàng hoá.
a) Xác định lượng hàng hoá được sản xuất khi mức giá bán 1 sản phẩm là 2 triệu đồng; 4 triệu đồng.
b) Biết nhu cầu thị trường đang cần là 600 sản phẩm. Hỏi với mức giá bán là bao nhiêu thì thị trường cân bằng (thị trường cân bằng khi sản lượng cung bằng sản lượng cầu)?
Vẽ đồ thị hàm số \(f(x) = 3x + 8\)
Xét hàm số \(y = f(x)\) cho bởi bảng sau:
|
\(x\) |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
\(f(x)\) |
8 |
3 |
0 |
-1 |
0 |
3 |
8 |
a) Tìm tập xác định D của hàm số trên.
b) Trong mặt phẳng tọa độ Oxy, vẽ tất cả các điểm có tọa độ (x; y) với \(x \in D\) và \(y = f(x).\)
Vẽ đồ thị hàm số \(f\left( x \right) = \left| x \right|\) biết rằng hàm số này còn được viết như sau:
\(f(x) = \left\{ \begin{array}{l}x\quad \quad (x \ge 0)\\ - x\quad \;\;(x < 0)\end{array} \right.\)
Cho đồ thị hàm số \(y = f\left( x \right)\) ở Hình 4. Phát biểu nào sau đây là đúng?
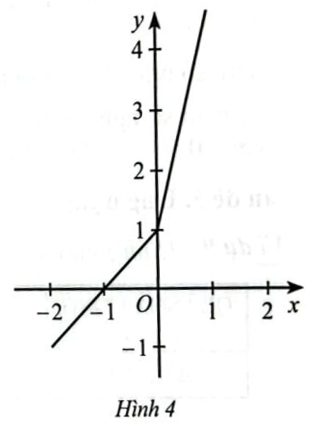
A. Đồ thị hàm số cắt trục hoành tại điểm của hoành độ bằng 1
B. Đồ thị hàm số cắt trục tung tại điểm có tung bộ bằng -1
C. Hàm số đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\), ngịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\)
D. Hàm số đồng biến trên \(\mathbb{R}\)
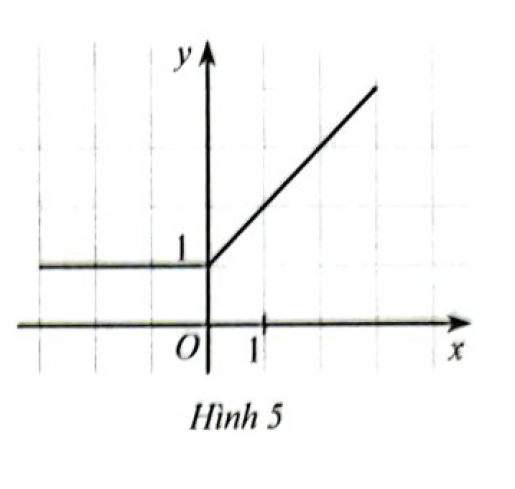
Quan sát đồ thị hàm số \(y = f\left( x \right)\) ở Hình 5.
a) Trong các điểm có tọa độ (1;2), (0;0). (2;3) điểm nào thuộc đồ thị hàm số, điểm nào không thuộc đồ thị hàm số?
b) Xác định \(f\left( 0 \right),f\left( 3 \right)\).
c) Tìm điểm thuộc đồ thị hàm số có tung độ bằng 1.
Cho hàm số \(y = f\left( x \right)\) có đồ thị ở Hình 24.
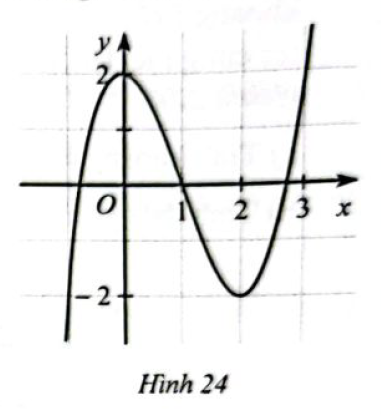
a) Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f\left( x \right)\).
b) Nêu tung độ giao điểm của đồ thị hàm số \(y = f\left( x \right)\) với trục \(Oy\).
Vẽ đồ thị các hàm số sau:
a) \(f\left( x \right) = \left\{ \begin{array}{l}{x^2}{\rm{ }}\quad x \le 2{\rm{ }}\\x + 2{\rm{ }}\quad x > 2\end{array} \right.\)
b) \(f\left( x \right) = \left| {x + 3} \right| - 2\)
Vẽ đồ thị hàm số sau: \(f\left( x \right) = \left\{ \begin{array}{l} - x + 1{\rm{ khi }}x < - 1\\1{\rm{ khi }} - 1 \le x < 1{\rm{ }}\\{x^2}{\rm{ khi }}x \ge 1\end{array} \right.\)
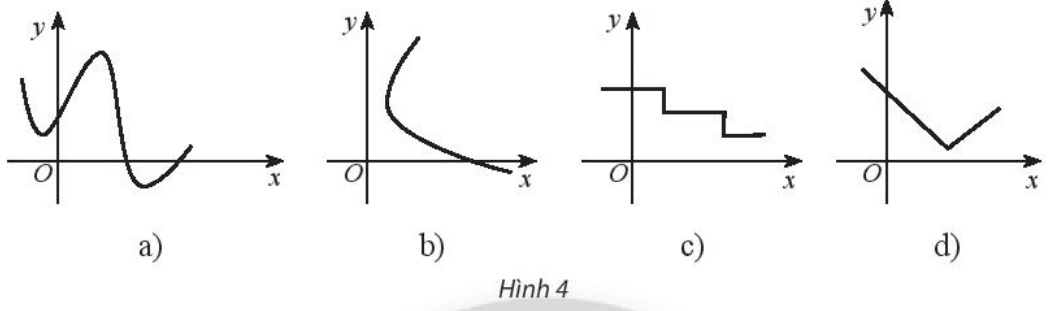
Trong các đường biểu diễn được cho trong hình 4, chỉ ra trường hợp không phải là đồ thị hàm số và giải thích vì sao
Nếu lượng điện tiêu thụ từ trên 50 đến 100 kWh (\(50 < x \le 100\)) thù công thức liên hệ giữa y và x đã thiết lập ở HĐ3 không còn đúng nữa.
Theo bảng giá bán lẻ điện sinh hoạt (Bảng 6.2) thì số tiền phải trả là:
\(y = 1,678.50 + 1,734(x - 50) = 83,9 + 1,734(x - 50)\), hay \(y = 1,734x - 2,8\)(nghìn đồng).
Vậy trên tập xác định \(D = (50;100{\rm{]}}\), hàm số y mô tả số tiền phải thanh toán có công thức là \(y = 1,734x - 2,8\); tập giá trị của nó là (83,9; 170,6].
Hãy vẽ đồ thị ở Hình 6.3 vào vở rồi vẽ tiếp đồ thị của hàm số \(y = 1,734x - 2,8\) trên tập \(D = (50;100{\rm{]}}\).
a) Dựa vào đồ thị \(y = \frac{1}{2}{x^2}\) (H.6.2), tìm x sao cho \(y = 8\)
b) Vẽ đồ thị của các hàm số \(y = 2x + 1\) và \(y = 2{x^2}\) trên cùng một mặt phẳng tọa độ.
Để đổi nhiệt độ từ thang Celsius sang thang Fahrenheit, ta nhân nhiệt độ theo thang Celsius với \(\frac{9}{5}\) sau đó cộng với 32.
a) Viết công thức tính nhiệt độ F ở thang Fahrenheit theo nhiệt độ C ở thang Celsius. Như vậy ta có F là một hàm số của C.
b) Hoàn thành bảng sau:
|
C (Celsius) |
-10 |
0 |
10 |
20 |
30 |
40 |
|
F (Fahrenheit) |
|
|
|
|
|
|
c) Vẽ đồ thị của hàm số F = F(C) trên đoạn [-10; 40].
Đồ thị trong hình vẽ dưới đây là của hàm số nào?
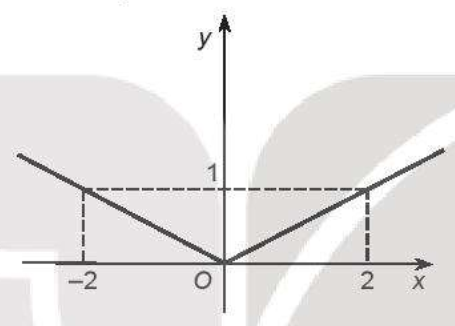
A. \(y = \left| {\frac{1}{2}x} \right|\)
B. \(y = \left| {3 - x} \right|\)
C. \(y = \left| x \right|\)
D. \(y = \left| {2x} \right|\)
Trục đối xứng của Parabol \((P):y = 2{x^2} + 6x + 3\) là:
A. y = -3
B. \(y = - \frac{3}{2}\)
C. x = -3
D. \(x = - \frac{3}{2}\)







Danh sách bình luận