Với giả thiết ở Bài tập 4, hãy:
a) Chứng minh rằng \(BC\parallel \left( {SAD} \right)\) và tính khoảng cách giữa \(BC\) và mặt phẳng \(\left( {SAD} \right)\).
b) Chứng minh rằng \(BD \bot \left( {SAC} \right)\) và tính khoảng cách giữa hai đường thẳng \(BD\) và \(SC\).
‒ Cách chứng minh đường thẳng song song với mặt phẳng: Chứng minh đường thẳng đó song song với một đường thẳng nằm trên mặt phẳng.
‒ Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song: Tính khoảng cách từ một điểm trên đường thẳng đến mặt phẳng.
‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng: Chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trên mặt phẳng.
‒ Cách tính khoảng cách giữa hai đường thẳng chéo nhau:
Cách 1: Dựng đường vuông góc chung.
Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.
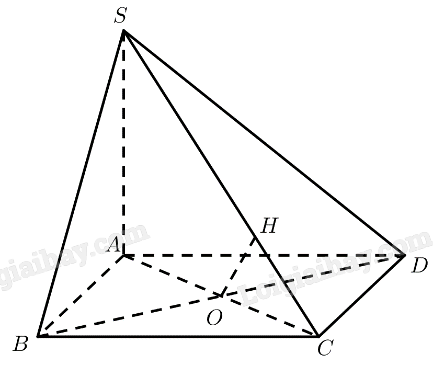
a) \(ABCD\) là hình vuông \( \Rightarrow BC\parallel A{\rm{D}}\)
Mà \(A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\)
\( \Rightarrow BC\parallel \left( {SAD} \right) \Rightarrow d\left( {BC,\left( {SAD} \right)} \right) = d\left( {B,\left( {SAD} \right)} \right)\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\)
\(ABCD\) là hình vuông \( \Rightarrow AB \bot A{\rm{D}}\)
\( \Rightarrow AB \bot \left( {SA{\rm{D}}} \right) \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\)
Vậy \(d\left( {BC,\left( {SAD} \right)} \right) = a\).
b) \(ABCD\) là hình vuông \( \Rightarrow B{\rm{D}} \bot A{\rm{C}}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot B{\rm{D}}\)
\( \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\)
Gọi \(O = AC \cap B{\rm{D}}\), kẻ \(OH \bot SC\left( {H \in SC} \right)\)
\(B{\rm{D}} \bot \left( {SAC} \right) \Rightarrow B{\rm{D}} \bot OH\)
\( \Rightarrow d\left( {B{\rm{D}},SC} \right) = OH\)
\(\Delta ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OC = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 \)
\(\Delta SAC \backsim \Delta OHC\,(g.g) \Rightarrow \frac{{SA}}{{OH}} = \frac{{SC}}{{OC}} \Rightarrow OH = \frac{{SA.OC}}{{SC}} = \frac{{a\sqrt 6 }}{6}\)
Vậy \(d\left( {B{\rm{D}},SC} \right) = \frac{{a\sqrt 6 }}{6}\).
Các bài tập cùng chuyên đề
Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77).
a) Tính khoảng cách từ A đến mặt phẳng (BCC'B').
b) Tam giác ABC' là tam giác gì? Tính khoảng cách từ A đến BC'.
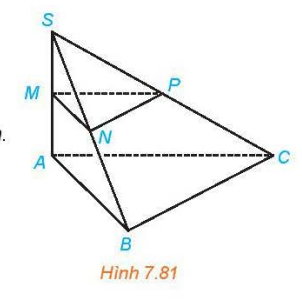
Cho hình chóp S.ABC có SA \( \bot \) (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) Tính d((MNP),(ABC)) và d(NP,(ABC)).
b) Giả sử tam giác ABC vuông tại B và AB = a. Tính d(A,(SBC)).
a) Cho hai đường thẳng m và n song song với nhau. Khi một điểm M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n có thay đổi hay không?
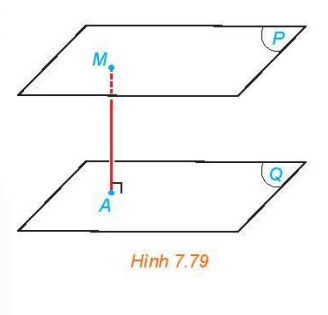
b) Cho hai mặt phẳng song song (P) và (Q) và một điểm M thay đổi trên (P) (H.7.79). Hỏi khoảng cách từ M đến (Q) thay đổi thế nào khi M thay đổi.
Khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia. Hãy thảo luận để làm rõ nhận xét này.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right),SA = a\sqrt 2 .\)
a) Tính khoảng cách từ A đến SC.
b) Chứng minh \(BD \bot \left( {SAC} \right).\)
c) Xác định đường vuông góc chung và tính khoảng cách giữa BD và SC.
Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) \( \bot \) (ABCD).
a) Tính chiều cao của hình chóp.
b) Tính khoảng cách giữa BC và (SAD).
c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, BC = c.
a) Tính khoảng cách giữa CC' và (BB'D'D).
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.
Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) MN là đường vuông góc chung của AB và CD.
b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.
Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình vuông cạnh \(a\). Cho biết \(SA = a\) và \(SA\) vuông góc với \(\left( {ABCD} \right)\).
a) Tính khoảng cách từ điểm \(B\) đến \(\left( {SAD} \right)\).
b) Tính khoảng cách từ điểm \(A\) đến cạnh \(SC\).
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tính khoảng cách:
a) Giữa hai mặt phẳng \(\left( {ACD'} \right)\) và \(\left( {A'C'B} \right)\).
b) Giữa đường thẳng \(AB\) và \(\left( {A'B'C'D'} \right)\).
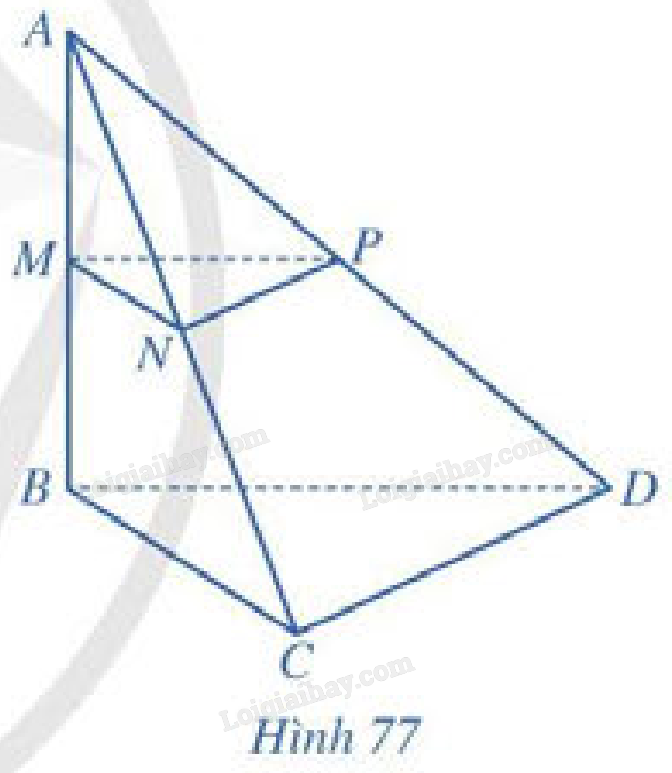
Cho hình tứ diện \(ABCD\) có \(AB = a,BC = b,BD = c\),\(\widehat {ABC} = \widehat {ABD} = \widehat {BCD} = {90^ \circ }\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,AC,AD\) (Hình 77).
a) Tính khoảng cách từ điểm \(C\) đến đường thẳng \(AB\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {ABC} \right)\).
c) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(CD\).
Với giả thiết ở Bài tập 2, hãy:
a) Chứng minh rằng \(MN\parallel BC\). Tính khoảng cách giữa hai đường thẳng \(MN\) và \(BC\).
b) Chứng minh rằng \(MP\parallel \left( {BCD} \right)\). Tính khoảng cách từ đường thẳng \(MP\) đến mặt phẳng \(\left( {BCD} \right)\).
c) Chứng minh rằng \(\left( {MNP} \right)\parallel \left( {BCD} \right)\). Tính khoảng cách giữa hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {BCD} \right)\).
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
a) Tính khoảng cách từ điểm \(S\) đến đường thẳng \(CD\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\).
c) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\).
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính theo a khoảng cách:
a) Giữa hai đường thẳng AB và C'D'.
b) Giữa đường thẳng AC và (A'B'C'D').
c) Từ điểm A đường thẳng B'D'.
d) Giữa hai đường thẳng AC và B'D'.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. \(SA \bot \left( {ABC} \right)\) và SA = 2a. Tính theo a khoảng cách:
a) Từ điểm B đến mặt phẳng (SAC).
b) Từ điểm A đến mặt phẳng (SBC).
c) Giữa hai đường thẳng AB và SC.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, góc ABC bằng \({60^ \circ }\), biết tam giác SBC đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính theo a khoảng cách:
a) Từ điểm S đến mặt phẳng (ABC).
b) Từ điểm B đến mặt phẳng (SAC).
c) Giữa hai đường thẳng AB và SC.
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, \(AD = a\sqrt 2\), \(AA' = a\sqrt 3 \). Tính theo a khoảng cách:
a) Từ điểm A đến mặt phẳng (BDD'B').
b) Giữa hai đường thẳng BD và CD'.
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A và AB = AC = AA' = a. Tính theo a khoảng cách:
a) Từ điểm A đến đường thẳng B'C'.
b) Giữa hai đường thẳng BC và AB'.
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), \(AB \bot BC\), \(SA = AB = 3a\), \(BC = 4a\). Tính khoảng cách:
a) Từ điểm \(C\) đến mặt phẳng \(\left( {SAB} \right)\).
b) Giữa hai đường thẳng \(SA\) và \(BC\).
c) Từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\).
d) Từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
e*) Giữa hai đường thẳng \(AB\) và \(SC\).
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật, \(AB = 2a\), \(AD = 3a\), tam giác \(\left( {SAB} \right)\) vuông cân tại \(S\) và nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right)\). Tính khoảng cách:
a) Từ điểm \(C\) đến mặt phẳng \(\left( {SAB} \right)\).
b) Giữa hai đường thẳng \(SB\) và \(CD\).
c) Giữa hai đường thẳng \(BC\) và \(SA\).
d) Từ điểm \(S\) đến mặt phẳng \(\left( {ABCD} \right)\).
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông cạnh \(a\), \(AC\) cắt \(BD\) tại \(O\), \(SO \bot \left( {ABCD} \right)\), \(SA = 2a\). Tính khoảng cách:
a) Từ điểm \(A\) đến mặt phẳng \(\left( {SBD} \right)\).
b) Giữa hai đường thẳng \(SO\) và \(CD\).
c) Từ điểm \(O\) đến mặt phẳng \(\left( {SCD} \right)\).
d*) Giữa hai đường thẳng \(AB\) và \(SD\).
Cho hình hộp \(ABCD.A'B'C'D'\) có \(ABCD\) là hình thoi cạnh \(a\), \(AA' \bot \left( {ABCD} \right)\), \(AA' = 2a\), \(AC = a\). Tính khoảng cách:
a) Từ điểm \(A\) đến mặt phẳng \(\left( {BCC'B'} \right)\).
b) Giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {CDD'C'} \right)\).
c*) Giữa hai đường thẳng \(BD\) và \(A'C\).
Cho khối tứ diện đều \(ABCD\) cạnh \(a\). Tính:
a) Khoảng cách giữa hai đường thẳng \(AB\) và \(CD\).
b) Chiều cao và thể tích của khối tứ diện đều \(ABCD\).
c) Côsin của góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\).
d) Côsin của số đo góc nhị diện \(\left[ {C,AB,D} \right]\).
