Trong Hình 1, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc trong không gian. Trong không gian, thế nào là hai đường thẳng vuông góc với nhau?

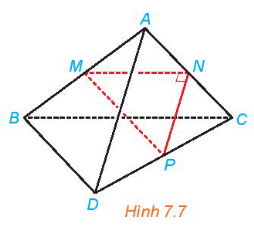
Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (H.7.7). Chứng minh rằng AD và BC vuông góc với nhau và chéo nhau.

Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b hay không?

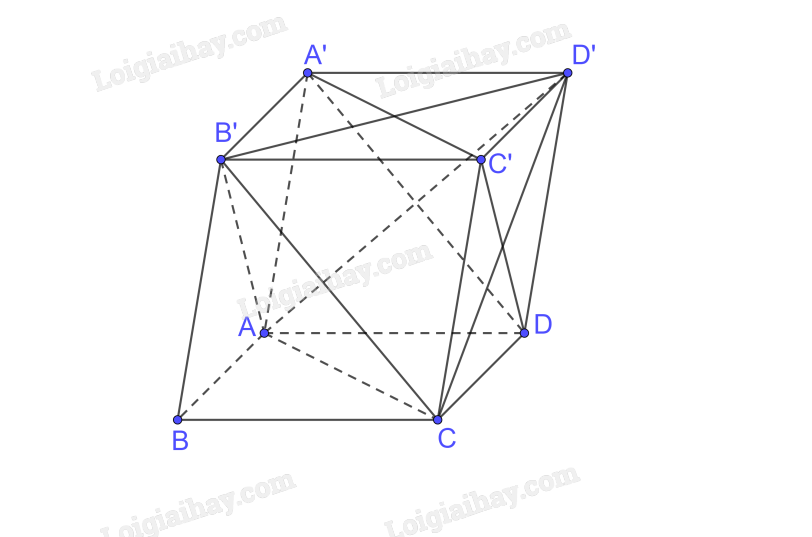
Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau. Chứng minh rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.

Cho tứ diện ABCD có \(\widehat {CBD} = {90^0}.\)

a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc BC.

b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng GK vuông góc với BC.

Đối với nhà gỗ truyền thống, trong các cấu kiện: hoành, quá giang, xà cái, rui, cột tương ứng được đánh số 1, 2, 3, 4, 5 như trong Hình 7.8, những cặp cấu kiện nào vuông góc với nhau?

Hình bên mô tả một người thợ đang ốp gạch vào tưởng có sử dụng thước laser để kẻ vạch. Tìm các đường thẳng vuông góc với đường thẳng \(a\) trong Hình 4. 

Cho tứ diện đều \(ABCD\). Chứng minh rằng \(AB \bot CD\).

Cho hình chóp \(S.ABC\) có \(SA = SB = SC = a,\widehat {BSA} = \widehat {CSA} = {60^ \circ },\) \(\widehat {BSC} = {90^ \circ }\). Cho \(I\) và \(J\) lần lượt là trung điểm của \(SA\) và \(BC\). Chứng minh rằng \(IJ \bot SA\) và \(IJ \bot BC\).

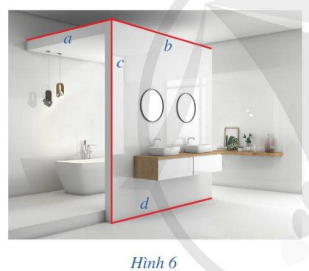
 Hình 6 gợi nên hình ảnh 5 cặp đường thẳng vuông góc. Hãy chỉ ra 5 cặp đường thẳng đó: 

Cho tứ diện \(ABCD\), gọi \(M\) và \(N\) lần lượt là trung điểm của \(AC\) và \(BD\). Biết \(MN = a\sqrt 3 ;AB = 2\sqrt 2 a\) và \(CD = 2a\). Chứng minh rằng đường thẳng \(AB\) vuông góc với đường thẳng \(CD\).

Cho tứ diện ABCD có AB = CD, AC = BD, AD = BC.

a) Chứng minh đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc hai cạnh đó.

b) Chứng minh hai đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với nhau.

Cho tứ diện đều ABCD cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh rằng hai đường thẳng OA và CD vuông góc với nhau.

Trong không gian, khẳng định nào sau đây đúng?

A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng vuông góc với đường thẳng thứ hai.

B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.

C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.

D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.

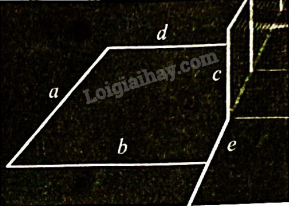
Hình 5 gợi nên hình ảnh một số cặp đường thẳng vuông góc với nhau. Hãy chỉ ra ba cặp đường thẳng vuông góc với nhau.

Cho hình hộp \(ABCD.A'B'C'D'\) có đáy là hình vuông.

a) Chứng minh rằng \(AB \bot A'D'\) và \(AC \bot B'D'.\)

b) Tính góc giữa hai đường thẳng \(AC\) và \(A'B'.\)

Cho hình lăng trụ MNPQ.M'N'P'Q' có tất cả các cạnh bằng nhau. Chứng minh rằng \(M'N \bot P'Q.\)

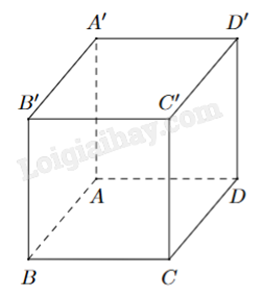
Cho hình hộp chữ nhật ABCD.A’B’C’D’ như hình vẽ bên. Cặp cạnh nào sau đây vuông góc với nhau nhưng không đồng phẳng?