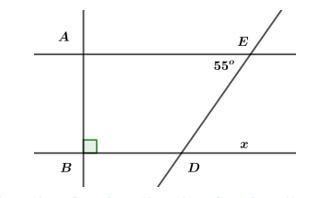
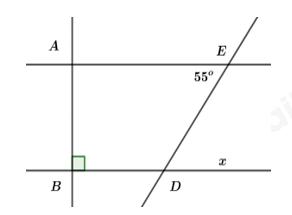
Cho hình vẽ, biết \(AE\,//\,BD,\,\angle ABD = {90^o},\,\angle AED = {55^o}.\) Số đo góc \(\angle BAE\) và \(\angle BDE\) lần lượt là:
A. \({90^o},\,{55^o}\)
B. \({90^o},\,{125^o}\)
C. \({55^o},\,{90^o}\)
D. \({35^o},\,{55^o}\)
- Nếu một đường thẳng cắt hai đường thẳng song song thì:
+ Hai góc so le trong bằng nhau;
+ Hai góc đồng vị bằng nhau.
- Dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt đường thẳng phân biệt ab, và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng hai thì a và b song song với nhau.
- Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì sẽ vuông góc với đường thẳng còn lại.
Ta có \(\angle ABD = {90^o}\left( {gt} \right) \Rightarrow AB \bot BD\)
Mà \(AE\,//\,BD\,\left( {gt} \right)\)
\( \Rightarrow AE \bot AB \Rightarrow \angle BAE = {90^o}\)
Vì \(AE\,//\,BD \Rightarrow \angle EDx = \angle AED = {55^o}\) (đối đỉnh)
Mà \(\angle BDE + \angle EDx = {180^o}\) (hai góc kề bù)
\( \Rightarrow \angle BDE = {180^o} - {55^o} = {125^o}\)
Chọn B.
