Trong hộp có 5 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 5. Lấy ra ngẫu nhiên lần lượt 2 thẻ từ hộp. Gọi \(A\) là biến cố “Thẻ lấy ra lần thứ nhất ghi số chẵn”; \(B\) là biến cố “Thẻ lấy ra lần thứ hai ghi số chẵn” và \(C\) là biến cố “Tích các số ghi trên hai thẻ lấy ra là số chẵn”.
Hãy viết tập hợp mô tả các biến cố trên.
Liệt kê các phần tử của tập hợp.
\(A = \left\{ {\left( {2;1} \right);\left( {2;3} \right);\left( {2;4} \right);\left( {2;5} \right);\left( {4;1} \right);\left( {4;2} \right);\left( {4;3} \right);\left( {4;5} \right)} \right\}\)
\(B = \left\{ {\left( {1;2} \right);\left( {1;4} \right);\left( {2;4} \right);\left( {3;2} \right);\left( {3;4} \right);\left( {4;2} \right);\left( {5;2} \right);\left( {5;4} \right)} \right\}\)
\(C = \left\{ {\left( {1;2} \right);\left( {1;4} \right);\left( {2;1} \right);\left( {2;3} \right);\left( {2;4} \right);\left( {2;5} \right);\left( {3;2} \right);\left( {3;4} \right);\left( {4;1} \right);\left( {4;2} \right);\left( {4;3} \right);\left( {4;5} \right);\left( {5;2} \right);\left( {5;4} \right)} \right\}\)

Các bài tập cùng chuyên đề
Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 12; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”. Phát biểu biến cố \(A \cup B\)dưới dạng mệnh đề nêu sự kiện.
Xét phép thử “Gieo ngẫu nhiên một xúc xắc cân đối và đồng chất một lần”. Gọi \(\Omega \) là không gian mẫu của phép thử đó. Xét hai biến cố A và B nêu trong bài toán ở phần mở đầu.
a) Viết các tập hợp con A, B của tập hợp \(\Omega \) tương ứng với các biến cố A, B.
b) Đặt \(C = A \cup B\). Phát biểu biến cố C dưới dạng mệnh đề nêu sự kiện.
Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 7” và biến cố B: “Số xuất hiện trên thẻ được rút là số chia hết cho 11”. Tính \(P\left( {A \cup B} \right)\).
Một tổ trong lớp 11B có 4 học sinh nữ là Hương, Hồng, Dung, Phương và 5 học sinh nam là Sơn, Tùng, Hoàng, Tiến, Hải. Trong giờ học, giáo viên chọn ngẫu nhiên một học sinh trong tổ đó lên bảng để kiểm tra bài. Xét các biến cố sau:
H: “Học sinh đó là một bạn nữ”;
K: “Học sinh đó có tên bắt đầu là chữ cái H”.
a) Mô tả không gian mẫu.
b) Nêu nội dung của biến cố hợp \(M = H \cup K.\) Mỗi biến cố H, K, M là tập con nào của không gian mẫu?
Một tổ trong lớp 11A có 10 học sinh. Điểm kiểm tra học kì I của 10 bạn này ở hai môn Toán và Ngữ văn được cho như sau:
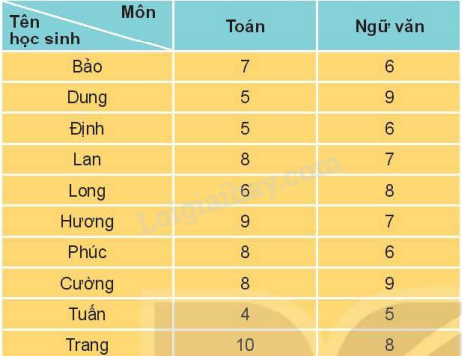
Chọn ngẫu nhiên một học sinh trong tổ. Xét các biến cố sau:
A: “Học sinh đó được điểm giỏi môn Ngữ văn”;
B: “Học sinh đó được điểm giỏi môn Toán”;
C: “Học sinh đó được điểm giỏi môn Ngữ văn hoặc điểm giỏi môn Toán”.
a) Mô tả không gian mẫu và các tập con A, B, C của không gian mẫu.
b) Tìm \(A \cup B\).
Gieo hai con xúc xắc cân đối, đồng chất. Xét các biến cố sau:
E: “Số chấm xuất hiện trên hai con xúc xắc đều là số chẵn”;
F: “Số chấm xuất hiện trên hai con xúc xắc khác tính chẵn lẻ”;
K: “Tích số chấm xuất hiện trên hai con xúc xắc là số chẵn”.
Chứng minh rằng K là biến cố hợp của E và F.
Một hộp đựng 20 tấm thẻ cùng loại được đánh số từ 1 đến 20. Rút ngẫu nhiên một tấm thẻ trong hộp. Gọi A là biến cố "Rút được tấm thẻ ghi số chẵn lớn hơn 9"; B là biến cố "Rút được tấm thẻ ghi số không nhỏ hơn 8 và không lớn hơn 15".
Số phần tử của \(A \cup B\) là
A. 11.
B. 10.
C. 12.
D. 13.
Một lớp học có 15 học sinh nam và 17 học sinh nữ. Chọn ra ngẫu nhiên 3 học sinh của lớp. Gọi \(A\) là biến cố “Cả 3 học sinh được chọn đều là nữ”, \(B\) là biến cố “Có 2 học sinh nữ trong 3 học sinh được chọn”.
a) Có bao nhiêu kết quả thuận lợi cho biến cố \(A\)? Có bao nhiêu kết quả thuận lợi cho biến cố \(B\)?
b) Hãy mô tả bằng lời biến cố \(A \cup B\) và tính số kết quả thuận lợi cho biến cố \(A \cup B\).
Cho \(A\) và \(B\) là hai biến cố độc lập. Biết \(P\left( A \right) = 0,4\) và \(P\left( B \right) = 0,5\). Xác suất của biến cố \(A \cup B\) là
A. 0,9.
B. 0,7.
C. 0,5.
D. 0,2.
Một hộp có 10 viên bi màu hồng và 14 viên bi màu vàng, các viên bi có kích thước và khối lượng như nhau. Lấy ngẫu nhiên hai viên bi. Xét các biến cố: P: “Hai viên bi được lấy ra có màu hồng”; Q: “Hai viên bi được lấy ra có màu vàng”.
Khi đó, biến cố hợp của hai biến cố P và Q là:
A. “Hai viên bi được lấy ra chỉ có màu hồng”.
B. “Hai viên bi được lấy ra có cùng màu”.
C. “Hai viên bi được lấy ra chỉ có màu vàng”.
D. “Hai viên bi được lấy ra có màu khác nhau”.
Một chiến hạm có ba bộ phận A, B, C có tầm quan trọng khác nhau. Chiến hạm sẽ bị chìm khi và chỉ khi:
- Hoặc có một quả ngư lôi bắn trúng bộ phận A;
- Hoặc có hai quả ngư lôi bắn trúng bộ phận B;
- Hoặc có ba quả ngư lôi bắn trúng bộ phận C.
Giả sử có hai quả ngư lôi bắn trúng chiến hạm. Xét hai biến cố \(K\) : "Hai quả trúng vào \({\rm{C}}\)",
\(H\) : "Một quả trúng vào \({\rm{B}}\), một quả trúng vào \({\rm{C}}\) ".
Gọi \(M\) là biến cố: "Chiến hạm không bị chìm". Chứng tỏ rằng \(M\) là biến cố hợp của \(H\) và \(K\).
Xét phép thử chọn ngẫu nhiên một số tự nhiên trong các số tự nhiên có một chữ số và hai biến cố A = {0;2;4;6;8} và B = {0;3;6;9}. Hỏi biến cố C là hợp của hai biến cố A và B là tập hợp gồm bao nhiêu phần tử?
-
A.
7
-
B.
9
-
C.
6
-
D.
8







Danh sách bình luận