Hình 96 minh họa một miếng bìa phẳng có dạng hình tam giác đặt thăng bằng trên đầu ngón tay tại điểm G.
Điểm G được xác định như thế nào?
Dựa vào Tính chất ba đường trung tuyến của tam giác để đưa ra cách xác định điểm G.
Điểm G được xác định bằng cách: lấy giao điểm của ba đường trung tuyến của tam giác.
Các bài tập cùng chuyên đề
Trong tam giác ABC ở ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB.
Trong tình huống mở đầu, người ta chứng minh được G chính là trọng tâm của tam giác ABC. Em hãy cắt một mảnh bìa hình tam giác. Xác định trọng tâm của tam giác và đặt mảnh bìa đó lên một giá nhọn tại trọng tâm vừa xác định. Quan sát xem mảnh bìa có thăng bằng không
Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp vào chỗ chấm hỏi để được các đẳng thức:
BG = ? BN, CG = ? CP;
BG = ? GN, CG = ? GP.
Chứng minh rằng:
a) Trong một tam giác cân, hai đường trung tuyến ứng với 2 cạnh bên là hai đoạn thẳng bằng nhau.
b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN.
Kí hiệu \({S_{ABC}}\) là diện tích tam giác ABC. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC.
a) Chứng minh \({S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\)
Gợi ý: Sử dụng \(GM = \dfrac{1}{3}AM\) để chứng minh \({S_{GMB}} = \dfrac{1}{3}{S_{ABM}},{S_{GCM}} = \dfrac{1}{3}{S_{ACM}}\).
b) Chứng minh \({S_{GCA}} = {S_{GAB}} = \dfrac{1}{3}{S_{ABC}}\).
a) Cắt một tam giác bằng giấy. Gấp lại để xác định trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này với đỉnh đối diện (Hình 4). Bằng cách tương tự, hãy vẽ tiếp hai đường trung tuyến còn lại.
Quan sát tam giác trên hình, em thấy ba đường trung tuyến vừa vẽ có cùng đi qua một điểm hay không.
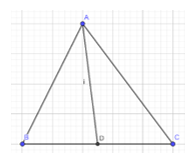
b) Em hãy đếm ô rồi vẽ lại tam giác ABC trong Hình 5 vào giấy kẻ ô vuông. Vẽ hai đường trung tuyến BE và CF của tam giác ABC. Hai đường trung tuyến này cắt nhau tại G. Tia AG cắt BC tại D.
Em hãy quan sát vào cho biết:
- AD có phải đường trung tuyến của tam giác ABC hay không?
- Các tỉ số \(\dfrac{{BG}}{{BE}}\), \(\dfrac{{CG}}{{CF}}\), \(\dfrac{{AG}}{{AD}}\) bằng bao nhiêu ?
Trong Hình 7, G là trọng tâm của tam giác AEF với đường trung tuyến AM.
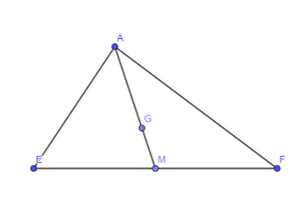
Hãy tính các tỉ số:
a) \(\dfrac{{GM}}{{AM}}\)
b) \(\dfrac{{GM}}{{AG}}\)
c) \(\dfrac{{AG}}{{GM}}\)
Cho tam giác ABC có O là trung điểm của BC, trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Gọi I và J lần lượt là trọng tâm của các tam giác ABC và BCD. Chứng minh rằng AI = IJ = JD.
Quan sát Hình 9
a) Biết AM = 15 cm, tính AG
b) Biết GN = 6 cm, tính CN
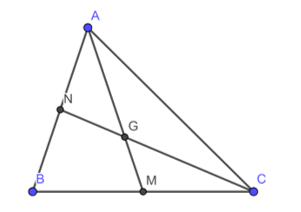
Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG.
a) Chứng minh rằng BG song song với EC.
b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI
Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.
a) Chứng minh rằng BM = CN
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC
Cho tam giác ABC có đường trung tuyến BM bằng đường trung tuyến CN. Chứng minh rằng tam giác ABC cân.
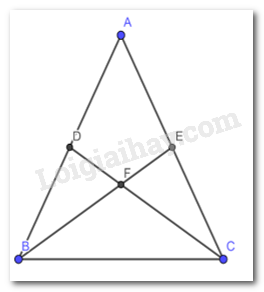
Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF.
Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.
a) Chứng minh rằng \(\Delta \)MFN = \(\Delta \)PFD
b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của GH. Gọi K là trung điểm của GK. Chứng minh rằng ba điểm M, H, K thẳng hàng.
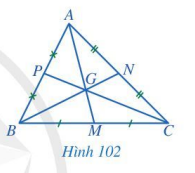
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 102, cho biết ba đường trung tuyến đó có cùng đi qua một điểm hay không.
Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.
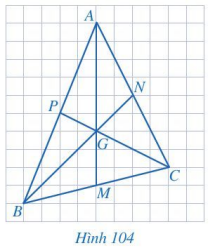
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 104. Bằng cách đếm số ô vuông, tìm các tỉ số
\(\dfrac{{AG}}{{AM}},\dfrac{{BG}}{{BN}},\dfrac{{CG}}{{CP}}\).
Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:
\(GA + GB + GC = \dfrac{2}{3}(AM + BN + CP)\).
Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:
a) BM = CN;
b) \(\Delta GBC\) cân tại G.
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:
a) \(\Delta AHB = \Delta AHM\);
b) \(AG = \dfrac{2}{3}AB\).
Hình 107 là mặt cắt đứng của một ngôi nhà ba tầng có mái dốc. Mỗi tầng cao 3,3 m. Mặt cắt mái nhà có dạng tam giác ABC cân tại A với đường trung tuyến AH dài 1,2 m. Tại vị trí O là trọng tâm tam giác ABC, người ta làm tâm cho một cửa sổ có dạng hình tròn.
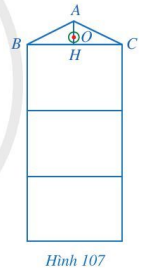
a) AH có vuông góc với BC không? Vì sao?
b) Vị trí O ở độ cao bao nhiêu mét so với mặt đất.
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Khi đó
A.\(AM = 2GM\).
B.\(AM = 2AG\).
C.\(GA = 3GM\).
D.\(GA = 2GM\).
