Chỉ ra các đường vuông góc, các đường xiên kẻ từ điểm I trong Hình 83a và từ điểm C trong Hình 83b.
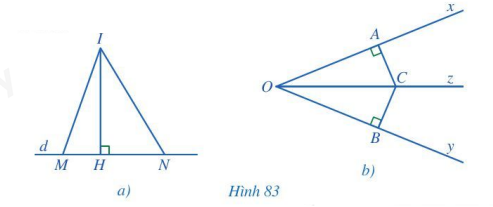
Nhận biết đường vuông góc, đường xiên.
Đường vuông góc kẻ từ điểm I là: IH.
Đường xiên kẻ từ điểm I là: IM, IN.
Đường vuông góc kẻ từ điểm C là: CA, CB.
Đường xiên kẻ từ điểm C là: CO.

Các bài tập cùng chuyên đề
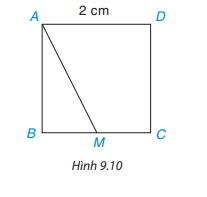
Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10
a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.
b) So sánh hai đoạn thẳng AB và AM.
c) Tìm khoảng cách từ điểm C đến đường thẳng AB.
Tình huống mở đầu
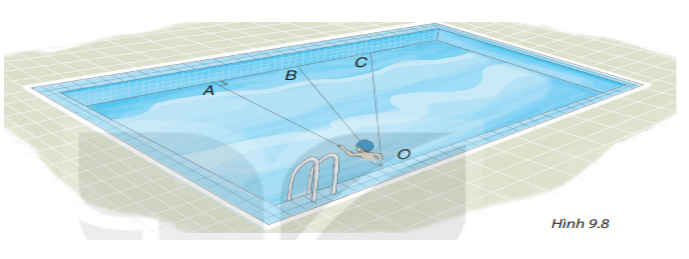
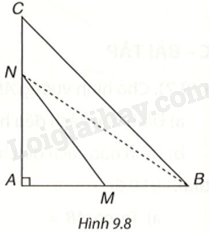
Bạn Nam tập bơi ở một bể bơi hình chữ nhật, trong đó có ba đường bơi OA, OB, OC. Biết rằng OA vuông góc với cạnh của bể bơi (H.9.8)
Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì bạn Nam nên chọn đường bơi nào?
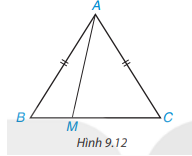
Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C. ( H. 9.12)
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
b) Chứng minh rằng với mọi điểm M thì AM < AB
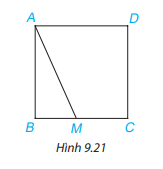
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc cạnh CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó. (H.9.21)
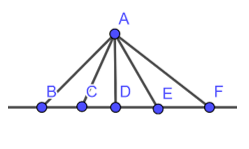
Trong Hình 8, tìm đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BF. Trong số các đường này, đường nào ngắn nhất ?
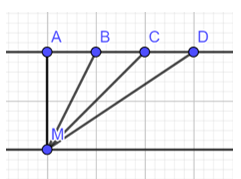
Bạn Minh xuất phát từ điểm M bên hồ bơi (Hình 9). Bạn ấy muốn tìm đường ngắn nhất để bơi đến thành hồ đối diện. Theo em, bạn Minh phải bơi theo đường nào ?
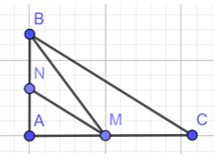
Quan sát Hình 10.
a) Tìm đoạn ngắn nhất trong các đoạn BA, BM, BC.
b) Tìm đoạn ngắn nhất trong các đoạn MA, MN, MB.
c) Chứng minh rằng MA < BC.
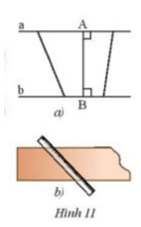
Trong Hình 11a, ta gọi độ dài đoạn thẳng AB là khoảng cách giữa hai đường thẳng song song a và b.
a) Một thanh nẹp gỗ có hai cạnh song song (Hình 11b). Chiều rộng của thanh nẹp gỗ là khoảng cách giữa hai cạnh đó. Hãy cho biết có phải chiều rộng của thanh nẹp gỗ là khoảng cách ngắn nhất từ một điểm trên cạnh này dến một điểm trên cạnh kia không.
b) Muốn đo chiều rộng của thanh nẹp, ta phải đặt thước như thế nào ? Vì sao?
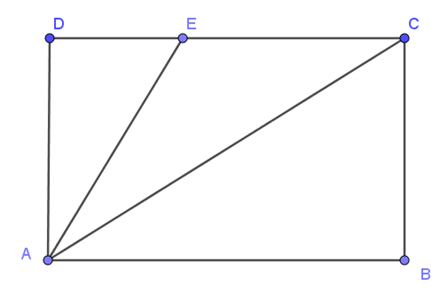
Cho \(ABCD\) là hình chữ nhật như hình vẽ, điểm \(E\) nằm trên cạnh \(CD\). Khẳng định nào sau đây là sai?
-
A.
\(AE < {\rm{ }}AD;\)
-
B.
\(AC > {\rm{ }}AD;\)
-
C.
\(AC >{\rm{ }}AE;\)
-
D.
\(AD < {\rm{ }}AE.\)
Cầu Bãi Cháy nối Hòn Gai và Bãi Cháy (Quảng Ninh). Trụ cầu và dây cáp của cầu gợi nên hình ảnh đường vuông góc và đường xiên.

Đường vuông góc và đường xiên có tính chất như thế nào?
Cho tam giác ABC vuông tại A.
a) Khoảng cách từ B đến đường thẳng AC bằng độ dài đoạn thẳng nào?
b) Đoạn thẳng nào là một đường xiên kẻ từ điểm B đến đường thẳng AC?
Cho tam giác nhọn ABC, \(\widehat B > \widehat C\). Gọi H là hình chiếu của A lên BC. Sắp xếp các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần.
Cho tam giác nhọn ABC.
a) Vẽ H là hình chiếu của B trên đường thẳng AC;
b) Vẽ K là hình chiếu của H trên đường thẳng AB;
c) Chứng minh rằng: HK < BH < BC.
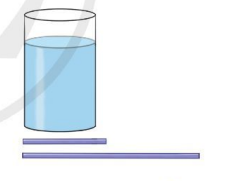
Trong một thí nghiệm khoa học, bạn Duy đặt hai chiếc đũa thủy tinh, một chiếc dài 14 cm và một chiếc dài 30 cm vào một bình thủy tinh có dạng hình trụ đựng dung dịch, cả hai đũa đều chạm đáy bình. Đường kính của đáy bình là 12 cm, chiều cao của dung dịch trong bình là 15 cm (bỏ qua bề dày của bình). Hỏi bạn Duy có thể cầm vào chiếc đũa thủy tinh nào mà ngón tay không bị chạm vào dung dịch? Vì sao?
Hình 85b mô tả mặt cắt đứng của một chiếc thang chữ A (Hình 85a), trong đó độ dài của một bên thang được tính bằng độ dài của đoạn thẳng OM, chiều cao của chiếc thang được tính bằng độ dài đoạn OH, với H là hình chiếu của điểm O trên đường thẳng d. Một người sử dụng thang này có thể đứng ở độ cao 4 m hay không nếu độ dài một bên thang là 3,5 m? Vì sao?

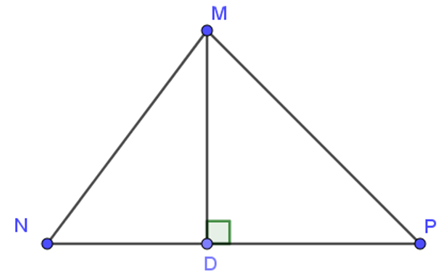
-
A.
DN = DP;
-
B.
MN = MP;
-
C.
MD > MN;
-
D.
MD < MP.
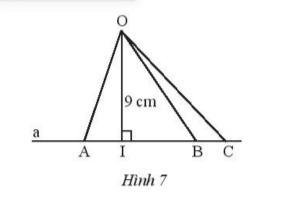
Trong hình 7,
a) Tìm đường ngắn nhất trong các đường OA, OI, OB, OC.
b) Tìm khoảng cách từ O đến đường thẳng a.
a) Chứng minh trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ cùng một đỉnh.
b) Chứng minh trong một tam giác, đường cao không lớn hơn đường phân giác xuất phát từ cùng một đỉnh.
Từ một điểm A nằm ngoài đường thẳng d, vẽ đường vuông góc AH và các đường xiên AB, AC tùy ý (Hình 40).

Cho tam giác ABC vuông tại A, M là trung điểm của AC.
a) Vẽ E là hình chiếu của A trên đường thẳng BM.
b) Vẽ F là hình chiếu của C trên đường thẳng BM.
c) Chứng minh BE + BF > 2AB.
Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh độ dài AD và DC.
Cho tam giác ABC vuông tại A (AB < AC), BD là tia phân giác của góc ABC (D ∈ AC). Qua C kẻ tia Cx vuông góc với AC cắt BD tại M.
a) Chứng minh tam giác CBM là tam giác cân.
b) So sánh độ dài CM và AC.
Cho tam giác ABC có \(\widehat B\) và \(\widehat C\) nhọn. H và K lần lượt là hình chiếu của B và C trên Ax (Hình 41).
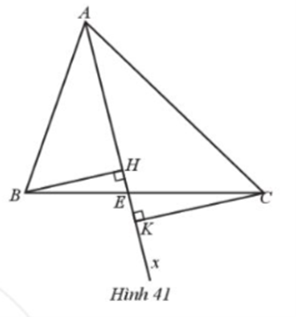
Cho tam giác ABC có đường cao AH. Khi đó:
A. \(AC < AH\).
B. \(AH > AB\).
C. \(AH < AC\).
D. Nếu \(\widehat B < \widehat C\) thì \(AC > AB\).
Cho Hình 9.5, kết luận nào sau đây là đúng?
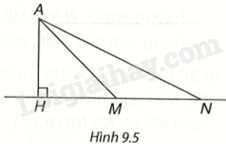
A. \(AH = AM\).
B. \(HM + MN > AN\).
C. \(HM > AM\).
D. \(AH < AN\).
Cho tam giác cân ABC, \(AB = AC\). Lấy điểm M tùy ý nằm giữa B và C (H.9.7).
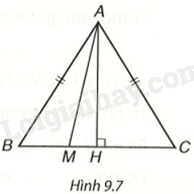
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
b) Chứng minh rằng với mọi điểm M thì \(AM < AB\).
Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC (M, N không phải là đỉnh của tam giác) (H.9.8). Chứng minh rằng \(MN < BC\). (Gợi ý. So sánh MN với NB, NB với BC).
Cho tam giác ABC. D là một điểm bất kì trên đoạn BC. Từ B, C kẻ các đường vuông góc BK, CN đến đường thẳng AD.
a) So sánh BK, BD.
b) So sánh \(BK + CN\) với BC.
c) Chứng minh \(BK + CN < \frac{1}{2}\left( {AB + BC + CA} \right)\).
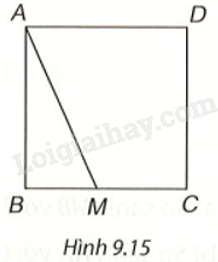
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (H.9.15).
Cho tam giác ABC có \(\widehat {BAC}\) là một góc tù. Lấy điểm D nằm giữa A và B; lấy điểm E nằm giữa A và C (H.9.43).
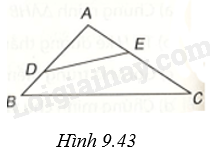
Chứng minh \(DE < BC\).