Lưới chắn bóng sân đá góp phần quan trọng vào việc bảo vệ sự an toàn cho các sân bóng cỏ nhân tạo. Vì vậy cần phải mắc hệ thống lưới bao quanh sân bóng đá. Có thể là lưới sợi dù, sợi nilon hay sợi nhựa, được gắn cố định vào cọc bê tông, gỗ hay cọc sắt. Một sân bóng đá mini ở phường Hiệp Bình Chánh có dạng hình chữ nhật (xem hình bên) có kích thước chiều dài 50m, chiều rộng 30m. Chủ sân cần mua lưới chắn sân với chiều cao lưới là 8m để bao quanh sân bóng.

a) Tính diện tích lưới cần mua?
b) Nếu mỗi mét vuông lưới có giá 20 000 đồng thì chủ sân cần trả bao nhiêu tiền để mua đủ lưới bao quanh sân bóng?
a) Diện tích lưới cần mua chính là diện tích xung quanh của hình hộp chữ nhật.
Sxq = Cđáy.chiều cao.
b) Số tiền mua lưới = Diện tích lưới . 20 000.
a) Diện tích lưới cần mua là:
\({S_{xq}} = \left( {50{\rm{ }} + {\rm{ }}30} \right).2.8 = 1280\left( {{m^2}} \right)\)
b) Số tiền mua lưới là:
\(1280.{\rm{ }}20{\rm{ }}000 = 25{\rm{ }}600{\rm{ }}000\) (đồng)

Các bài tập cùng chuyên đề
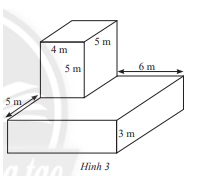
Một khối bê tông, được đặt trên mặt đất có kích thước như hình 3
a) Người ta muốn sơn tất cả các mặt của khối bê tông, trừ mặt tiếp giáp với mặt đất. Hỏi chi phí để sơn là bao nhiêu? Biết rằng để sơn mỗi mét vuông tốn 25 nghìn đồng.
b) Tính thể tích của khối bê tông.
Phần bên trong của một cái khuôn làm bánh có dạng hình hộp chữ nhật với đáy là hình vuông cạnh 20 cm, chiều cao 5 cm ( Hình 3). Người ta dự định sơn phần bên trong bằng loại sơn không dính. Hỏi với một lượng sơn đủ bao phủ được 100 m2 thì sơn được bao nhiêu cái khuôn làm bánh?
Một hình hộp chữ nhật có chiều dài, chiều cao và diện tích xung quanh lần lượt là 8 m; 5 m và 100 \(m^2\). Chiều rộng của hình hộp chữ nhật là:
-
A.
3 m;
-
B.
2 m;
-
C.
4 m;
-
D.
1 m.
Một phòng học hình hộp chữ nhật có chiều dài 8 m, chiều rộng 5 m, chiều cao 4 m. Người ta quét vôi bên trong lớp học, kể cả trần. Biết tổng diện tích các cửa ra vào và cửa sổ là 10 m2. Tính diện tích phải quét vôi.
Một căn phòng có dạng hình hộp chữ nhật với chiều dài là 5 m, chiều rộng là 3,2 m, chiều cao là 3 m. Người ta muốn sơn phía trong bốn bức tường và cả trần của căn phòng. Tính số tiền người đó phải trả, biết rằng diện tích của các cửa của căn phòng đó là 7 m2 và giá tiền sơn mỗi mét vuông (bao gồm tiền công và nguyên vật liệu) là 10 500 đồng.
Một bể bơi có dạng hình hộp chữ nhật với chiều dài là 12 m, chiều rộng là 5 m, chiều sâu là 1,75 m. Người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh bể đó? Biết rằng mỗi viên gạch có dạng hình chữ nhật với chiều dài là 25 cm, chiều rộng là 20 cm và diện tích mạch vữa không đáng kể.
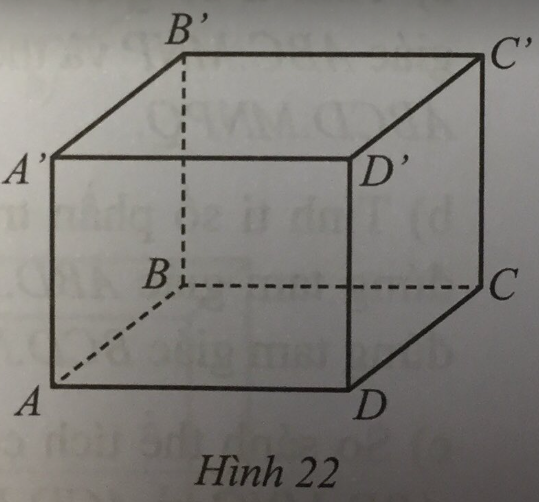
Cho hình hộp chữ nhật ABCD.A’B’C’D’ với các kích thước \(AB = 20{\rm{ cm}}\), \(BC = 15{\rm{ cm}}\), \(CC' = 12{\rm{ cm}}\) (Hình 22). Tính tỉ số diện tích xung quanh và tổng diện tích hai đáy của hình hộp chữ nhật đó là:
A. \(\dfrac{5}{{14}}\)
B. \(\dfrac{7}{5}\).
C. \(\dfrac{5}{7}\).
D. \(\dfrac{{14}}{5}\).
Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một cửa sổ hình vuông với các kích thước như hình vẽ.
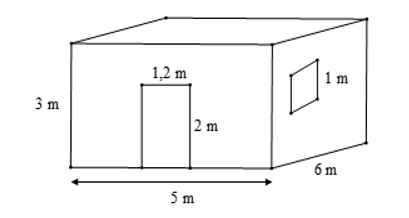
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.
Cho hình hộp chữ nhật có kích thước như hình vẽ.
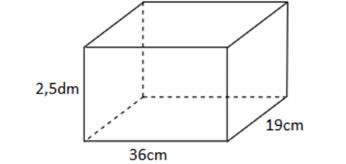
Diện tích xung quanh của hình hộp chữ nhật là:
-
A.
\(2750 \ cm^{2}\)
-
B.
\(275 \ cm^{2}\)
-
C.
\(2770 \ cm^{2}\)
-
D.
\(27 \ cm^{2}\)
Tính tổng diện tích các hình chữ nhật (1), (2), (3), (4). So sánh kết quả vừa tìm với tích của chu vi đáy và chiều cao của hình hộp chữ nhật.
Bác Tú thuê thợ sơn xung quanh bốn mặt ngoài của thành bể nước có dạng hình hộp chữ nhật có chiều dài 3 m, chiều rộng 2 m, chiều cao 1,5 m với giá 20,000đồng /m2 . Hỏi bác Tú phải chi trả chi phí là bao nhiêu?

Người ta xếp một số viên gạch dạng hình hộp chữ nhật tạo thành một khối hình lập phương cạnh 20 cm như hình 10.44.
a) Tính diện tích xung quanh và diện tích toàn phần của khối hình lập phương.
b) Tìm kích thước mỗi viên gạch.

Một căn phòng dạng hình hộp chữ nhật có chiều dài 5m , chiều rộng 4 m và chiều cao 3 m. Người ta muốn lăn sơn tường và trần nhà . Hỏi diện tích cần lăn sơn bao nhiêu mét vuông, biết rằng tổng diện tích các cửa bằng 5,8 m2 ?
Diện tích xung quanh của hình hộp chữ nhật có độ dài hai đáy là \(6\,cm;\,\,8\,cm\) và chiều cao \(10\,cm\) là:
-
A.
\(6.8.10\,\left( {c{m^2}} \right)\).
-
B.
\(\left( {6 + 8} \right).10\,\left( {c{m^2}} \right)\).
-
C.
\(6 + 8 + 10\,\left( {c{m^2}} \right)\).
-
D.
\(2.\left( {6 + 8} \right).10\,\left( {c{m^2}} \right)\).
Một thùng đựng hàng bằng thép không có nắp dạng hình hộp chữ nhật có chiều dài 2m, chiều rộng 1,5m và chiều cao 2m. Người thợ cần bao nhiêu ki-lô-gam sơn để sơn bên ngoài các mặt xung quanh chiếc thùng đó? Biết rằng với mỗi ki-lô-gam sơn sẽ sơn được \(4{m^2}\) mặt thùng.
Một thùng đựng hàng có nắp dạng hình hộp chữ nhật có chiều dài 3m, chiều rộng 2m và chiều cao 1,8m. Người thợ cần bao nhiêu kilogam sơn để đủ sơn toàn bộ mặt ngoài của chiếc thùng đó, biết rằng mỗi kilogam sơn có thể sơn được 5 m2 mặt thùng.
Một bể bơi có chiều dài 12m, chiều rộng 5m và sâu 2,75 m. Hỏi người thợ phải dùng bao nhiêu viên gạch men hình chữ nhật để lát đáy và xung quanh thành bể đó? Biết rằng diện tích mạch vữa lát không đáng kể và mỗi viên gạch có chiều dài 25 cm, chiều rộng 20 cm.
Một căn phòng dạng hình hộp chữ nhật có chiều dài 5m, chiều rộng 4m và chiều cao 3m. Người ta muốn lăn sơn tường và trần nhà. Hỏi diện tích cần lăn sơn là bao nhiêu mét vuông, biết rằng tổng diện tích các cửa bằng \(5,8{m^2}\)?
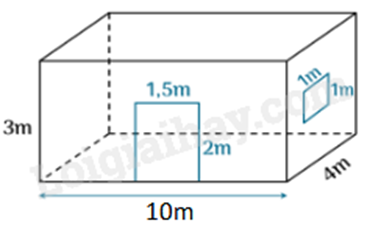
a) Tính thể tích của thùng.
b) Người thợ phải tốn bao nhiêu tiền mua sơn để đủ sơn các mặt xung quanh của chiếc thùng? Biết rằng mỗi kg sơn sơn được 9m2 và giá tiền 1kg sơn có giá 250 000 đồng.







Danh sách bình luận