Tính:
a) \( - 2{x^2} + 6{x^2}\);
b) \(4{x^3} - 8{x^3}\);
c) \(3{x^4}( - 6{x^2})\)
d) \(( - 24{x^6}):( - 4{x^3})\).
Với phép cộng (trừ) các đơn thức có cùng biến và lũy thừa của biến, ta giữ nguyên biến và số mũ lũy thừa của nó rồi thực hiện phép tính (cộng, trừ) giữa các hệ số đi cùng.
Với phép nhân (chia) các đơn thức, ta nhân (chia) hệ số của các biến với nhau, và nhân (chia) biến với nhau:
\({x^m}.{x^n} = {x^{m + n}};{x^m}:{x^n} = {x^{m - n}}\) (với m > n).
a) \( - 2{x^2} + 6{x^2} = ( - 2 + 6).{x^2} = 4{x^2}\);
b) \(4{x^3} - 8{x^3} = (4 - 8).{x^3} = - 4{x^3}\);
c) \(3{x^4}( - 6{x^2}) = 3.( - 6).{x^4}.{x^2} = - 18{x^{4 + 2}} = - 18{x^6}\);
d) \(( - 24{x^6}):( - 4{x^3}) = ( - 24: - 4).({x^6}:{x^3}) = 6{x^{6 - 3}} = 6{x^3}\).

Các bài tập cùng chuyên đề
Rút gọn biểu thức sau:
(5x3 – 4x2) : 2x2 + (3x4 + 6x) : 3x – x(x2 – 1)
Rút gọn các biểu thức sau:
a) 2x(x+3) – 3x2(x+2) + x(3x2 + 4x – 6)
b) 3x(2x2 – x) – 2x2(3x+1) + 5(x2 – 1)
Thực hiện các phép tính sau:
a) (x3 – 8) : (x – 2)
b) (x – 1)(x + 1)(x2 + 1)
Trong một trò chơi ở câu lạc bộ Toán học, chủ trò viết lên bảng biểu thức:
P(x) = x2 (7x – 5) – (28x5 – 20x4 – 12x3) : 4x2
Luật chơi là sau khi chủ trò đọc một số a nào đó, các đội chơi phải tìm giá trị của P(x) tại x = a. Đội nào tính đúng và tính nhanh nhất thì thắng cuộc.
Khi chủ trò vừa đọc a = 5, Vuông đã tính ngay được P(a) = 15 và thắng cuộc. Em có biết Vuông làm cách nào không?
Cho đa thức A = x4 + x3 – 2x – 2
a) Tìm đa thức B sao cho A + B = x3 + 3x + 1
b) Tìm đa thức C sao cho A – C = x5
c) Tìm đa thức D biết rằng D = (2x2 – 3) . A
d) Tìm đa thức P sao cho A = (x+1) . P
e) Có hay không một đa thức Q sao cho A = (x2 + 1) . Q?
Tính:
a) \(({x^2} + 2x + 3) + (3{x^2} - 5x + 1)\);
b) \((4{x^3} - 2{x^2} - 6) - ({x^3} - 7{x^2} + x - 5)\);
c) \( - 3{x^2}(6{x^2} - 8x + 1)\);
d) \((4{x^2} + 2x + 1)(2x - 1)\);
e) \(({x^6} - 2{x^4} + {x^2}):( - 2{x^2})\);
g) \(({x^5} - {x^4} - 2{x^3}):({x^2} + x)\).
Nhân dịp lễ Giáng sinh, một cửa hàng bán quần áo trẻ em thông báo khi mua mỗi bộ quần áo sẽ được giảm 30% so với giá niêm yết. Giả sử giá niêm yết mỗi bộ quần áo là x (đồng). Viết biểu thức tính số tiền phải trả khi mua loại quần áo đó với số lượng:
a) 1 bộ;
b) 3 bộ;
c) y bộ.
Cho đa thức \(A\left( x \right) = - 11{x^5} + 4x - 12{x^2} + 11{x^5} + 13{x^2} - 7x + 2\)
a) Thu gọn, sắp xếp đa thức \(A(x)\) theo số mũ giảm dần của biến rồi tìm bậc, hệ số cao nhất của đa thức.
b) Tìm đa thức \(M(x)\) sao cho \(M(x) = A(x).B(x)\), biết \(B(x) = x - 1\).
c) Tìm nghiệm của đa thức \(A(x)\).
Thực hiện các phép tính sau:
\(a)\left( {5{x^3} - 2{x^2} + 4x - 4} \right)\left( {3{x^2} + x - 1} \right)\)
\(b)\left( {9{x^5} - 6{x^3} + 18{x^2} - 35x - 42} \right):\left( {3{x^3} + 5x + 6} \right);\)
\(c)\left[ {\left( {6{x^3} - 5{x^2} - 8x + 5} \right) - \left( {4{x^2} - 6x + 2} \right)} \right]:\left( {2x - 3} \right).\)
Rút gọn các biểu thức sau:
\(a)A = \left( {x - 1} \right)\left( {x + 2} \right)\left( {x - 3} \right) - \left( {x + 1} \right)\left( {x - 2} \right)\left( {x + 3} \right)\)
b)\(B = \left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right)\left( {{x^4} + 1} \right) - {x^8}.\)
Rút gọn các biểu thức sau:
a) \(4\left( {2y - 3x} \right) - 3\left( {x - 2y} \right)\)
b) \({x^2} + 5y - 2y - 7{x^2}\)
Tính giá trị của mỗi biểu thức sau:
a) \(3(2x - 1) + 5(3 - x)\) tại \(x = - \frac{3}{2}\)
b) \(2x(6x - 1) - 3x(4x - 1)\) tại \(x = \) -2 022
c) \((x - 2)({x^2} + x + 1) - x({x^2} - 1)\) tại x = 0,25
d) \(2{x^2} + 3(x - 1)(x + 1)\) tại \(x = \frac{1}{3}\)
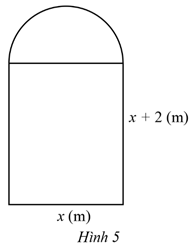
Một ngôi nhà có 4 ô cửa sổ, mỗi ô cửa sổ được mô tả như Hình 5 gồm một hình chữ nhật có độ dài các cạnh là x (m), x + 2 (m) và một nửa hình tròn. Người ta muốn ốp kính cường lực cho các ô cửa sổ đó. Hỏi cần bao nhiêu mét vuông kính (lấy \(\pi \) = 3,14)? Biết diện tích của phần khung gỗ là 0,42 m2.
Tính:
a) \(( - 4{x^3} - 13{x^2} + 2{x^5}) + (13{x^2} + 2{x^3} - 12x - 1)\)
b) \((12{x^6} - 11{x^2} + 3{x^3} + 9) - (13{x^5} + 2{x^3} - 11{x^2} - 11x)\)
c) \((8{x^3} - {x^2} + 1)({x^2} - 1)\)
d) \((8{x^3} + 6{x^2} + 3x + 1):(2x + 1)\)
Giá bán lẻ 1 hộp sữa là 7 000 đồng, giá cho 1 lốc sữa 4 hộp là 26 000 đồng. Nếu mua từ 4 lốc sữa trở lên thì cứ 2 lốc sữa được tặng 1 hộp. Vậy nếu bác Hoa mua 2a \((a \in \mathbb{N},2 \le a < 10)\) lốc sữa thì sẽ tiết kiệm bao nhiêu tiền so với mua lẻ từng hộp?
Nhân dịp cuối năm, một cửa hàng cần thanh lí một lô hàng (gồm 100 sản phẩm cùng loại) với giá bán là x đồng/chiếc. Lần đầu cửa hàng giảm 10% so với giá bán thì bán được 15 sản phẩm, lần sau cửa hàng giảm thêm 5% nữa (so với giá đã giảm lần đầu) thì bán được hết 85 sản phẩm còn lại. Viết biểu thức biểu thị số tiền cửa hàng thu được sau khi đã bán hết 100 sản phẩm trên.
Rút gọn biểu thức sau:
\(\left( {5{x^3} - 4{x^2}} \right):2{x^2} + \left( {3{x^4} + 6x} \right):3x - x\left( {{x^2} - 1} \right)\).
Tìm giá trị của x, biết rằng:
a) \(3{x^2} - 3x\left( {x - 2} \right) = 36\).
b) \(5x\left( {4{x^2} - 2x + 1} \right) - 2x\left( {10{x^2} - 5x + 2} \right) = - 36\).
Thực hiện các phép tính sau:
a) \(\left( {{x^3} - 8} \right):\left( {x - 2} \right)\);
b) \(\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right)\).
Cho đa thức \(A = {x^4} + {x^3} - 2x - 2\).
a) Tìm đa thức B sao cho \(A + B = {x^3} + 3x + 1\).
b) Tìm đa thức C sao cho \(A - C = {x^5}\).
c) Tìm đa thức D sao cho \(D = \left( {2{x^2} - 3} \right).A\).
d) Tìm đa thức P sao cho \(A = \left( {x + 1} \right).P\).
e) Có hay không một đa thức Q sao cho \(A = \left( {{x^2} + 1} \right).Q\)?
a) Tìm đa thức A, biết rằng \(\left( {4{x^2} + 9} \right).A = 16{x^4} - 81\).
b) Tìm đa thức M sao cho \(\left( {27{x^3} + 8} \right):M = 3x + 2\).
Cho đa thức \(F\left( x \right) = {x^4} - {x^3} - 6{x^2} + 15x - 9\)
a)Kiểm tra lại rằng x = 1 và x = -3 là hai nghiệm của F(x).
b)Tìm đa thức G(x) sao cho \(F\left( x \right) = \left( {x - 1} \right)\left( {x + 3} \right).G\left( x \right)\)
Cho hai đa thức \(A = 6{x^3} - 4{x^2} - 12x - 7\) và \(B = 2{x^2} - 7\).
a) Xác định hệ số cao nhất và hệ số tự do trong mỗi đa thức đã cho.
b) Tính giá trị của đa thức \(A + B\) tại \(x = - 2\).
c) Chứng minh rằng \(x = 0,x = - 1\) và \(x = 2\) là ba nghiệm của đa thức \(A - B\).
d) Trình bày phép nhân A.B bằng hai cách.
e) Tìm đa thức R có bậc nhỏ hơn 2 sao cho hiệu \(A - R\) chia hết cho B.
Người ta đổ đầy nước vào một cái bể hình hộp chữ nhật, sau đó nhấn chìm một khối lập phương (đặc) có độ dài các cạnh bằng x(dm) vào trong bể. Biết rằng chiều rộng, chiều dài và chiều cao của bể lần lượt bằng \(x + 1,x + 3\) và \(x + 2\) (xem dưới đây).
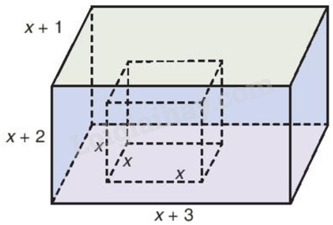
a) Tìm đa thức biểu thị lượng nước còn lại trong bể.
b) Xác định bậc, hệ số cao nhất và hệ số tự do của đa thức trong câu a.
c) Sử dụng kết quả câu a để tính lượng nước còn lại trong bể (đơn vị \(d{m^3}\)) khi \(x = 7\left( {dm} \right)\).
\(Q\left( x \right) = 2{x^3}\; - 4{x^2} + 3x - 6\)
a) Tính \(P(x) - Q(x)\)
b) Chứng tỏ rằng x = 2 là nghiệm của cả hai đa thức P(x) và Q(x).
\(P\left( x \right) = - 2x + \dfrac{1}{2}{x^2} + 3{x^4} - 3{x^2} - 3\)
\(Q\left( x \right) = 3{x^4} + {x^3} - 4{x^2} + 1,5{x^3} - 3{x^4} + 2x + 1\)
a) Thu gọn và sắp xếp các đa thức trên theo thứ tự số mũ của biến giảm dần. Xác định bậc, hệ số cao nhất và hệ số tự do của các đa thức đã cho.
b) Xác định \(P\left( x \right) + Q\left( x \right)\),\(P\left( x \right) - Q\left( x \right)\).
c) Xác định đa thức \(R\left( x \right)\) thỏa mãn \(R\left( x \right) + P\left( x \right) - Q\left( x \right) + {x^2} = 2{x^3} - \dfrac{3}{2}x + 1\).
Tìm đa thức bị chia biết đa thức chia là \(\left( {{x^2} + x + 1} \right)\), thương là \(\left( {x + 3} \right)\), dư là \(x - 2\):
-
A.
\({x^3} + 4{x^2} + 5x + 1\)
-
B.
\({x^3} - 4{x^2} + 5x + 1\)
-
C.
\({x^3} - 4{x^2} - 5x + 1\)
-
D.
\({x^3} + 4{x^2} - 5x + 1\)
\(P\left( x \right) = 3 + 2{x^2} - 5x - 1 + 5{x^3} + 7x\)
\(Q\left( x \right) = - 9x + 5{x^3} + {x^2} + 2 + x\).
a) Thu gọn và sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến.
b) Tính \(G\left( x \right) = P\left( x \right) + Q\left( x \right)\); \(H\left( x \right) = P\left( x \right) - Q\left( x \right)\).
c) Tìm nghiệm của đa thức \(H\left( x \right)\).
\(A\left( x \right) = 9{x^4} + 2{x^2} - x + 6\);
\(B\left( x \right) = - 8{x^4} - 2{x^2} + 4{x^3} + 3 - 5{x^3}\).
a) Thu gọn và sắp xếp đa thức \(B\left( x \right)\) theo luỹ thừa giảm dần của biến.
b) Chứng tỏ \(x = 9\) là nghiệm của đa thức \(P\left( x \right) = A\left( x \right) + B\left( x \right) - {x^4} + {x^3}\).
a) Tính \(P\left( x \right) + Q\left( x \right)\).
b) Tìm đa thức \(A\left( x \right)\)sao cho \(A\left( x \right) + 2.Q\left( x \right) = P\left( x \right)\).







Danh sách bình luận