Cho hình chóp cụt tứ giác đều có cạnh đáy lớn bằng \(2a\), cạnh đáy nhỏ và đường nối tâm hai đáy bằng \(a\). Tính độ dài cạnh bên và đường cao của mỗi mặt bên.
Sử dụng định lí Pitago.
Gọi \(O\) và \(O'\) lần lượt là tâm của hai đáy.
Kẻ \(B'H \bot B{\rm{D}}\left( {H \in B{\rm{D}}} \right),B'K \bot BC\left( {K \in BC} \right)\)
\(\begin{array}{l}B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = 2a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = a\sqrt 2 \\B'D' = \sqrt {A'B{'^2} + A'{\rm{D}}{{\rm{'}}^2}} = a\sqrt 2 \Rightarrow B'O' = \frac{1}{2}B'{\rm{D'}} = \frac{{a\sqrt 2 }}{2}\end{array}\)
\(OO'B'H\) là hình chữ nhật \( \Rightarrow OH = B'O' = \frac{{a\sqrt 2 }}{2},B'H = OO' = a\)
\( \Rightarrow BH = BO - OH = \frac{{a\sqrt 2 }}{2}\)
Tam giác \(BB'H\) vuông tại \(H\) có: \(BB' = \sqrt {B'{H^2} + B{H^2}} = \frac{{a\sqrt 6 }}{2}\)
\(BCC'B'\) là hình thang cân \( \Rightarrow BK = \frac{{BC - B'C'}}{2} = \frac{a}{2}\)
Tam giác \(BB'K\) vuông tại \(K\) có: \(B'K = \sqrt {BB{'^2} - B{K^2}} = \frac{{a\sqrt 5 }}{2}\)
Các bài tập cùng chuyên đề
Hình chóp cụt đều có các cạnh bên bằng nhau hay không?
Cho hình chóp đều S.A1A2...An. Một mặt phẳng không đi qua S và song song với mặt phẳng đáy, cắt các cạnh SA1, SA2,.... SAn, tương ứng tai B1, B2,..., Bn
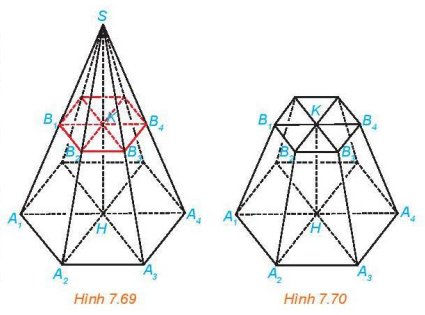
a) Giải thích vì sao S. B1B2...Bn là một hình chóp đều.
b) Gọi H là tâm của đa giác A1A2...An. Chứng minh rằng đường thẳng SH đi qua tâm K của đa giác đều B1B2...Bn, và HK vuông góc với các mặt phẳng (A1A2...An), (B1B2...Bn)
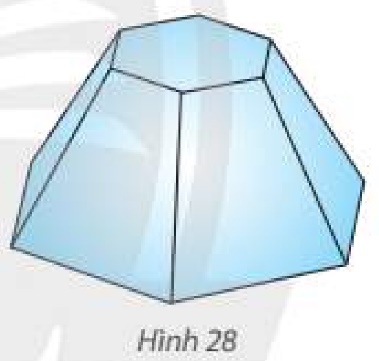
Một người cần sơn tất cả các mặt của một cái bục để đặt tượng có dạng hình chóp cụt lục giác đều có cạnh đáy lớn 1 m, cạnh bên và cạnh đáy nhỏ bằng 0,7 m. Tính tổng diện tích cần sơn.
Cho hình chóp cụt tam giác đều \(ABC.A'B'C'\) có cạnh đáy lớn \(a\), cạnh đáy nhỏ \(\frac{a}{2}\) và cạnh bên \(2a\). Tính độ dài đường cao của hình chóp cụt đó.
Cho hình chóp đều \(S.{A_1}{A_2}{A_3}...{A_6}\). Mặt phẳng \(\left( P \right)\) song song với mặt đáy và cắt các cạnh bên lần lượt tại \({A_1}^\prime ,{A_2}^\prime ,{A_3}^\prime ,...,{A_6}^\prime \).
a) Đa giác \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \) có phải lục giác đều không? Giải thích.
b) Gọi \(O\) và \(O'\) lần lượt là tâm của hai lục giác \({A_1}{A_2}{A_3}...{A_6}\) và \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \). Đường thẳng \(OO'\) có vuông góc với mặt đáy không?
Cho hình chóp đều \(S.ABC\). Gọi \(A',B',C'\) lần lượt là trung điểm của các đoạn thẳng \(SA,SB,SC\). Chứng minh rằng phần hình chóp đã cho giới hạn bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\) là hình chóp cụt đều.
Khối bê tông ở Hình 87a gợi nên hình ảnh một hình chóp bị cắt đi bởi mặt phẳng \(\left( R \right)\) song song với đáy. Hình 87b là hình biểu diễn của khối bê tông ở Hình 87a. Hãy dự đoán về mối quan hệ giữa các đường thẳng chứa các cạnh \({A_1}{B_1},{A_2}{B_2},{A_3}{B_3},{A_4}{B_4}\).
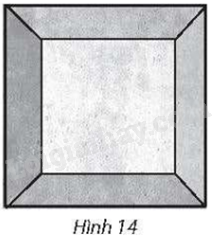
Người ta cần sơn tất cả các mặt của một khối bê tông hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 2m, đáy nhỏ có cạnh bằng 1m và cạnh bên bằng 2m (Hình 14). Tính tổng diện tích các bề mặt cần sơn.
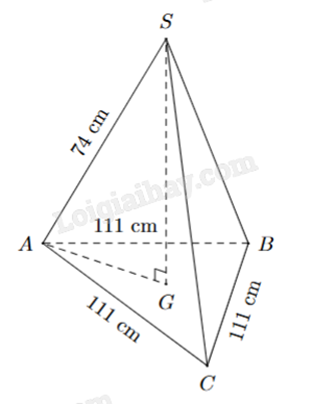
Một tripod (giá đỡ điện thoại, máy ảnh) được thiết kế và đặt như hình vẽ. Chiều cao của tripod là bao nhiêu?
