Mục tiêu
Vận dụng kiến thức về đại lượng tỉ lệ để nhận biết các đại lượng tỉ lệ thuận và tỉ lệ nghịch trong thực tế. Qua đó ôn tập và củng cố các tính chất cơ bản của các đại lượng tỉ lệ.
Chuẩn bị
- Chia lớp theo nhóm học tập từ 8 đến 10 học sinh.
- Mỗi nhóm chuẩn bị một tờ bìa có ghi hai bảng thống kê theo mẫu.
Tiến hành hoạt động
- Nhóm trưởng phân công một số bạn trong nhóm tìm các đại lượng tỉ lệ thuận và tỉ lệ nghịch trong thực tế để ghi vào hai bảng.
- Nhóm trưởng cùng các bạn còn lại kiểm tra và ghi thông tin vào các cột theo yêu cầu trong bảng.
- Các nhóm báo cáo trước lớp.
- Giáo viên cho nhận xét và đánh giá theo ba tiêu chí: đúng, đầy đủ và phong phú.
Chú ý:
- Có thể cho các nhóm bốc thăm để mỗi nhóm chỉ cần tìm một loại đại lượng tỉ lệ thuận hoặc tỉ lệ nghịch.
- Học sinh có thể truy cập vào internet để tìm kiếm các đại lượng tỉ lệ và làm trang trình chiếu minh họa.
Ví dụ minh họa:
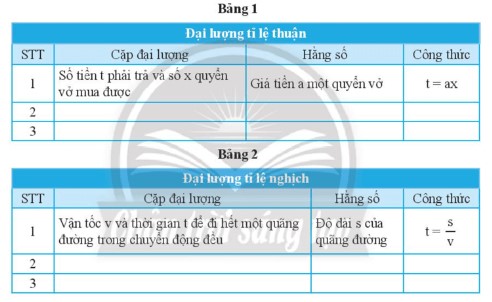
Bảng 1
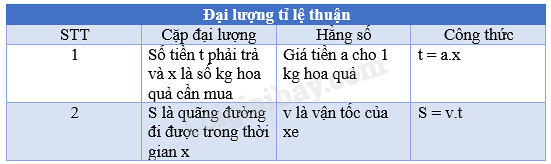
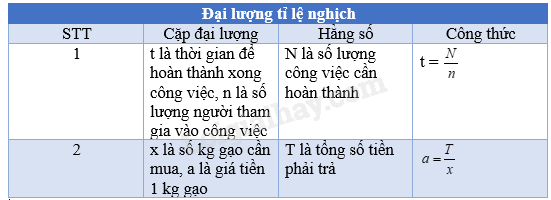
Bảng 2

Các bài tập cùng chuyên đề
Tượng Nữ thần Tự do ở Mĩ cao 151 ft 1 in (không kể bệ tượng).
(Theo nps.gov)
Hãy tính chiều cao của tượng Nữ thần Tự do theo đơn vị mét (làm tròn đến hàng đơn vị).
Dưới đây là một số thông tin về khối lượng của tượng Nữ thần Tự do.

Hãy đổi các thông tin khối lượng trên sang đơn vị tấn (làm tròn đến chữ số thập phân thứ hai).
Dưới đây là một số thông số kĩ thuật của một dòng máy bay.

Hãy đổi các thông số kĩ thuật trên sang các đơn vị đo lường quen thuộc là mét (riêng tầm bay đổi sang kilômét) và kilôgam (làm tròn kết quả đến hàng đơn vị).
Thực hành tính toán việc tăng, giảm theo giá trị phần trăm của một mặt hàng
Trong đợt khuyến mãi, một cửa hàng quần áo giảm giá 15% tất cả các sản phẩm.
a) Viết công thức tính giá mới của một mặt hàng theo giá cũ.
b) Nếu một chiếc áo phông có giá niêm yết là 300 nghìn đồng thì giá của nó sau khi giảm là bao nhiêu?
Trong tài chính, Quy tắc 72 là quy tắc tính nhẩm dùng để ước tính khoảng thời gian cần thiết để số vốn đầu tư ban đầu có thể tăng lên gấp đôi dựa vào mức lãi suất hằng năm cố định. Quy tắc này cho bởi công thức \(t = \dfrac{72}{r}\) , trong đó t là thời gian tính bằng năm, r% mỗi năm là lãi suất kép (tức là cứ sau mỗi năm số tiền lãi của năm đó được cộng vào số tiền gốc cũ để được số tiền gốc mới, dùng để tính lãi cho năm tiếp theo).
a) Một khoản đầu tư sẽ tăng gấp đôi trong bao lâu nếu lãi suất kép là 6% mỗi năm?
b) Bác Nam có 100 triệu đồng và bác muốn đầu tư để tăng gấp đôi số tiền của mình sau 5 năm. Hỏi lãi suất kép cho khoản đầu tư đó phải là bao nhiêu?
Lãi suất kì hạn 12 tháng của một ngân hàng là 5,6%/năm.
a) Viết công thức tính số tiền lãi thu được sau một năm theo số tiền gửi.
b) Bác Hà gửi 120 triệu đồng với kì hạn 12 tháng ở ngân hàng đó. Hỏi sau một năm bác Hà nhận được bao nhiêu tiền cả gốc lẫn lãi?
c) Giả sử lãi suất không thay đổi, hãy dùng Quy tắc 72 ước lượng số năm cần gửi tiết kiệm để số tiền gửi của bác Hà tăng gấp đôi.







Danh sách bình luận