Thực hiện phép nhân.
a) \((4x - 3)(x + 2)\)
b) \((5x + 2)( - {x^2} + 3x + 1)\)
c) \((2{x^2} - 7x + 4)( - 3{x^2} + 6x + 5)\)
Áp dụng các quy tắc nhân đa thức ( phân phối )
a) \((4x - 3)(x + 2) = 4x(x + 2) - 3(x + 2)\)
\(= 4{x^2} + 8x - 3x - 6\)
\( = 4{x^2} + 5x - 6\)
b) \((5x + 2)( - {x^2} + 3x + 1)\)
\( = 5x( - {x^2} + 3x + 1) + 2( - {x^2} + 3x + 1)\)
\( = - 5{x^3} + 15{x^2} + 5x - 2{x^2} + 6x + 2\)
\( = - 5{x^3} + 13{x^2} + 11x + 2\)
c) \((2{x^2} - 7x + 4)( - 3{x^2} + 6x + 5)\)
\( = 2{x^2}( - 3{x^2} + 6x + 5) - 7x( - 3{x^2} + 6x + 5) + 4( - 3{x^2} + 6x + 5)\)
\( = 2{x^2}( - 3{x^2}) + 2{x^2}.6x + 2{x^2}.5 + 7x.3{x^2} - 7x.6x - 7x.5 + 4( - 3{x^2}) + 4.6x + 4.5\)
\(= - 6{x^4} + 33{x^3} - 44{x^2} - 11x + 20\)
Các bài tập cùng chuyên đề
Tính (2x – 3) . (x2 – 5x + 1) bằng cách thực hiện các bước sau:
Bước 1: Nhân 2x với đa thức x2 – 5x + 1
Bước 2: Nhân (-3) với đa thức x2 – 5x + 1
Bước 3: Cộng các đa thức thu được ở hai bước trên và thu gọn
Kết quả thu được là tích của đa thức 2x – 3 với đa thức x2 – 5x + 1
Tính (x3 – 2x2 + x – 1)(3x – 2). Trình bày lời giải theo 2 cách.
Rút gọn biểu thức (x – 2) . (2x3 – x2 + 1) + (x – 2) x2(1 – 2x)
Trở lại bài toán đoán tuổi, để giải thích bí mật trong bài toán đoán tuổi của anh Pi, em hãy thực hiện các yêu cầu sau:
* Gọi x là tuổi cần đoán. Tìm đa thức ( biến x) biểu thị kết quả thứ nhất và kết quả thứ hai
* Tìm đa thức biểu thị kết quả cuối cùng.
Từ đó hãy nêu cách tìm x.
Thực hiện phép nhân sau:
a) (x2 – x) . (2x2 – x – 10)
b) (0,2x2 – 3x) . 5(x2 -7x + 3)
a) Tính (x2 – 2x + 5) . (x – 2)
b) Từ đó hãy suy ra kết quả phép nhân (x2 – 2x + 5) . (2– x). Giải thích cách làm.
Giả sử ba kích thước của một hình hộp chữ nhật là x; x +1; x – 1 ( cm) với x > 1. Tìm đa thức biểu thị thể tích ( đơn vị: cm3) của hình hộp chữ nhật đó.
Thực hiện các phép nhân hai đa thức sau:
a) 5x3 – 2x2 + 4x – 4 và x3 + 3x2 – 5
b) -2,5.x4 + 0,5x2 + 1 và 4x3 – 2x + 6
Người ta dùng những chiếc cọc để rào một mảnh vườn hình chữ nhật sao cho mỗi góc vườn đều có một chiếc cọc và hai cọc liên tiếp cắm cách nhau 0,1 m. Biết rằng số cọc dùng để rào hết chiều dài của vườn nhiều hơn số cọc dùng để rào hết chiều rộng là 20 chiếc. Gọi số cọc dùng để rào hết chiều rộng là x . Tìm đa thức biểu thị diện tích của vườn đó.
Thực hiện phép nhân \((4x - 3)(2{x^2} + 5x - 6)\)
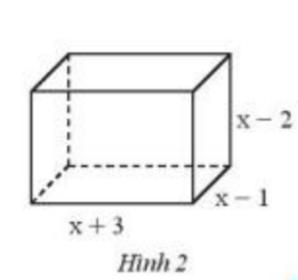
Tìm đa thức theo biến x biểu thị thể tích của hình hộp chữ nhật có kích thước như Hình 2.
Thực hiện phép tính \(\dfrac{1}{5}.({x^2} + 1).5\)
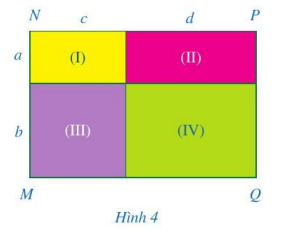
Cho hai hình chữ nhật như Hình 4. Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh
Thực hiện phép nhân.
a) \((3x - 2)(4x + 5)\)
b) \(({x^2} - 5x + 4)(6x + 1)\)
Trong quá trình biến đổi và tính toán những biểu thức đại số, nhiều khi ta phải thực hiện phép nhân hai đa thức một biến, chẳng hạn ta cần thực hiện phép nhân sau:
\((x - 1)({x^2} + x + 1)\)
Làm thế nào để thực hiện được phép nhân hai đa thức một biến?
Quan sát hình chữ nhật MNPQ ở Hình 4.
a) Tính diện tích mỗi hình chữ nhật (I), (II), (III), (IV).
b) Tính diện tích của hình chữ nhật MNPQ.
c) So sánh: \((a + b)(c + d)\) và \(ac + ad + bc + bd\).
Cho đa thức \(P(x) = 2x + 3\) và đa thức \(Q(x) = x + 1\).
a) Hãy nhân mỗi đơn thức của đa thức P(x) với từng đơn thức của đa thức Q(x).
b) Hãy cộng các tích vừa tìm được.
Tính:
a) \(({x^2} - 6)({x^2} + 6)\);
b) \((x - 1)({x^2} + x + 1)\).
Tính:
a) \(\dfrac{1}{2}{x^2}.\dfrac{6}{5}{x^3}\);
b) \({y^2}(\dfrac{5}{7}{y^3} - 2{y^2} + 0,25)\);
c) \((2{x^2} + x + 4)({x^2} - x - 1)\);
d) \((3x - 4)(2x + 1) - (x - 2)(6x + 3)\).
Tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức:
a) \(P(x) = ( - 2{x^2} - 3x + x - 1)(3{x^2} - x - 2)\);
b) \(Q(x) = ({x^5} - 5)( - 2{x^6} - {x^3} + 3)\).
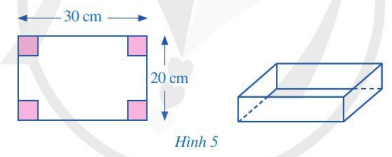
Từ tấm bìa hình chữ nhật có kích thước 20 cm và 30 cm, bạn Quân cắt đi ở mỗi góc của tấm bìa một hình vuông sao cho bốn hình vuông bị cắt đi có cùng độ dài cạnh, sau đó gấp lại để tạo thành hình hộp chữ nhật không nắp (Hình 5). Viết đa thức biểu diễn thể tích của hình hộp chữ nhật được tạo thành theo độ dài cạnh của hình vuông bị cắt đi.
