a) Xét hàm số mũ \(y = {2^x}\) với tập xác định \(\mathbb{R}\).
i) Hoàn thành bảng giá trị sau:

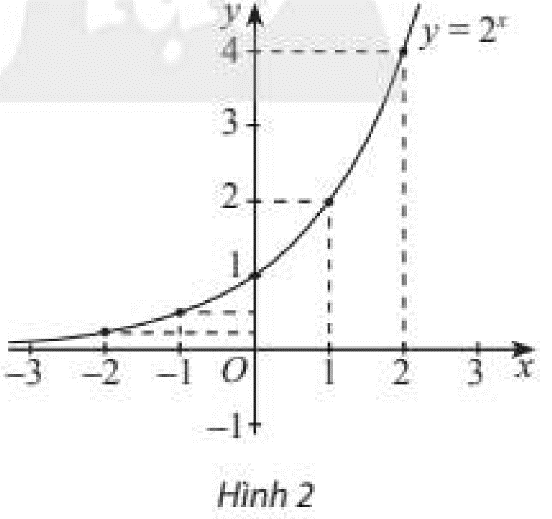
ii) Trong mặt phẳng toạ độ \(Oxy\), xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm \(M\left( {x;{2^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị hàm số \(y = {2^x}\) như Hình 2. Từ đồ thị nảy, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to - \infty \) và tập giá trị của hàm số đã cho.
b) Lập bảng giá trị và vẽ đồ thị của hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\). Từ đó, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to - \infty \) và tập giá trị của hàm số này.
a) Thay các giá trị của \(x\) vào hàm số sau đó dựa vào đồ thị nhận xét.
b) Lập bảng giá trị, vẽ đồ thị hàm số, sau đó dựa vào đồ thị nhận xét.
a) i)

ii) ‒ Hàm số liên tục trên \(\mathbb{R}\).
‒ Hàm số đồng biến trên \(\mathbb{R}\).
‒ Giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {2^x} = + \infty ;\mathop {\lim }\limits_{x \to - \infty } {2^x} = 0\).
‒ Tập giá trị: \(\left( {0; + \infty } \right)\).
b) Bảng giá trị:

Đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\):
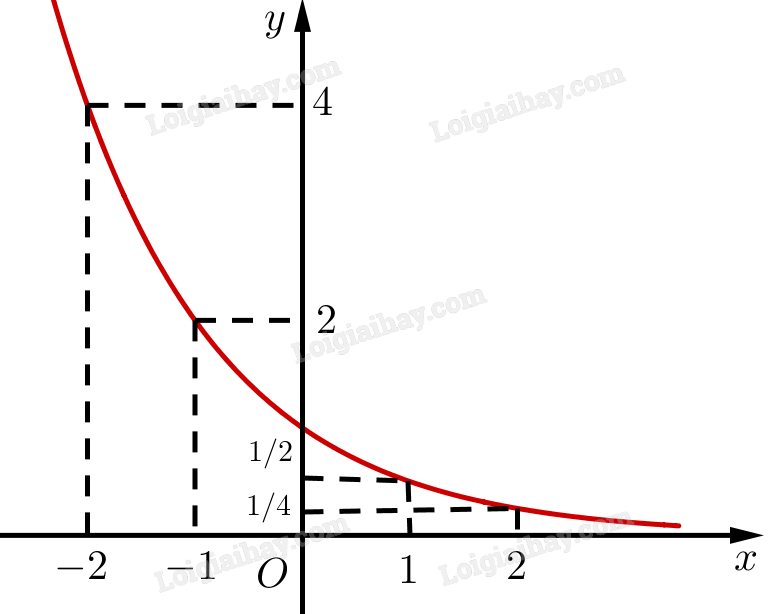
‒ Hàm số liên tục trên \(\mathbb{R}\).
‒ Hàm số nghịch biến trên \(\mathbb{R}\).
‒ Giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{1}{2}} \right)^x} = 0;\mathop {\lim }\limits_{x \to - \infty } {\left( {\frac{1}{2}} \right)^x} = + \infty \).
‒ Tập giá trị: \(\left( {0; + \infty } \right)\).

Các bài tập cùng chuyên đề
Vẽ đồ thị của hàm số \(y = {\left( {\frac{3}{2}} \right)^x}.\)
Cho hàm số mũ \(y = {2^x}.\)
a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; 2x) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị của hàm số.
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số.
Trong các hàm số sau, những hàm số nào là hàm số mũ? Khi đó hãy chỉ ra cơ cố.
a) \(y = {\left( {\sqrt 2 } \right)^x};\)
b) \(y = {2^{ - x}};\)
c) \(y = {8^{\frac{x}{3}}};\)
d) \(y = {x^{ - 2}}.\)
a) Tính \(y = {2^x}\) khi x lần lượt nhận các giá trị - 1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của \(y = {2^x}\) tương ứng?
b) Với những giá trị nào của x, biểu thức \(y = {2^x}\) có nghĩa?
Vẽ đồ thị của các hàm số sau:
a) \(y = {3^x};\)
b) \(y = {\left( {\frac{1}{3}} \right)^x}.\)
Cho hàm số \(y = {2^x}\). Khẳng định nào sau đây là sai?
A. Tập xác định của hàm số là \(\mathbb{R}\).
B. Tập giá trị của hàm số là \((0; + \infty )\).
C. Đồ thị của hàm số cắt trục Ox tại đúng một điểm.
D. Hàm số đồng biến trên tập xác định của nó.
Khối lượng vi khuẩn của một mẻ nuôi cấy sau \(t\) giờ kể từ thời điểm ban đầu được cho bởi công thức \(M\left( t \right) = 50.1,{06^t}\left( g \right)\).
(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, năm 2017, trang 101)
a) Tìm khối lượng vi khuẩn tại thời điểm bắt đầu nuôi cấy (gọi là khối lượng ban đầu).
b) Tính khối lượng vi khuẩn sau 2 giờ và sau 10 giờ (làm tròn kết quả đến hàng phần trăm).
c) Khối lượng vi khuẩn tăng dần hay giảm dần theo thời gian? Tại sao?
So sánh các cặp số sau:
a) \(0,{85^{0,1}}\) và \(0,{85^{ - 0,1}}\).
b) \({\pi ^{ - 1,4}}\) và \({\pi ^{ - 0,5}}\).
c) \(\sqrt[4]{3}\) và \(\frac{1}{{\sqrt[4]{3}}}\).
Trên cùng một hệ trục toạ độ, vẽ đồ thị các hàm số \(y = {3^x}\) và \(y = {\left( {\frac{1}{3}} \right)^x}\).
Nguyên phân là quá trình tế bào phân chia thành hai tế bào con giống hệt nhau về mặt di truyền.
Lập bảng sau đây để tính số tế bào được tạo ra từ một tế bào ban đầu sau những lần nguyên phân.

a) Hoàn thành bảng trên vào vở.
b) Gọi \(y\) là số tế bào được tạo ra từ một tế bào ban đầu sau \(x\left( {x = 0,1,2,...} \right)\) lần nguyên phân. Viết công thức biểu thị \(y\) theo \(x\).
Vẽ đồ thị các hàm số sau:
a) \(y = {4^x}\);
b) \(y = {\left( {\frac{1}{4}} \right)^x}\).
So sánh các cặp số sau:
a) \(1,{3^{0,7}}\) và \(1,{3^{0,6}}\);
b) \(0,{75^{ - 2,3}}\) và \(0,{75^{ - 2,4}}\).
Cường độ ánh sáng \(I\) dưới mặt biển giảm dần theo độ sâu theo công thức \(I = {I_0}.{a^d}\), trong đó \({I_0}\) là cường độ ánh sáng tại mặt nước biển, \(a\) là hằng số \(\left( {a > 0} \right)\) và \(d\) là độ sâu tính bằng mét tính từ mặt nước biển.
(Nguồn: https://www.britannica.com/science/seawer/Optical-properties)
a) Có thể khẳng định rằng \(0 < a < 1\) không? Giải thích.
b) Biết rằng cường độ ánh sáng tại độ sâu 1 m bằng \(0,95{I_0}\). Tìm giá trị của \(a\).
c) Tại độ sâu 20 m, cường độ ánh sáng bằng bao nhiêu phần trăm so với \({I_0}\)? (Làm tròn kết quả đến hàng đơn vị.)
Cho \(\alpha ,\beta \) là hai số thực với \(\alpha < \beta \). Khẳng định nào sau đây đúng?
A. \({\left( {0,3} \right)^\alpha } < {\left( {0,3} \right)^\beta }\).
B. \({\pi ^\alpha } \ge {\pi ^\beta }\).
C. \({\left( {\sqrt 2 } \right)^\alpha } < {\left( {\sqrt 2 } \right)^\beta }\).
D. \({\left( {\frac{1}{2}} \right)^\beta } > {\left( {\frac{1}{2}} \right)^\alpha }\).
Biết \({4^\alpha } + {4^{ - \alpha }} = 5\).
Tính giá trị của các biểu thức:
a) \({2^\alpha } + {2^{ - \alpha }}\);
b) \({4^{2\alpha }} + {4^{ - 2\alpha }}\).
Cho đồ thị ba hàm số mũ \(y = {a^x},y = {b^x}\) và \(y = {c^x}\) như trong hình vẽ dưới đây. Khẳng định nào sau đây là đúng?
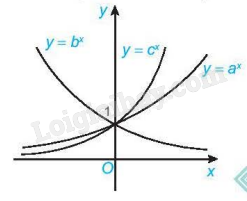
A. \(a > c > b\).
B. \(b > a > c\).
C. \(c > a > b\).
D. \(c > b > a\).
Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\).
Cho hai ví dụ về hàm số mũ.
Cho hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.
Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{{\left( {\frac{1}{2}} \right)}^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) (Hình 2)
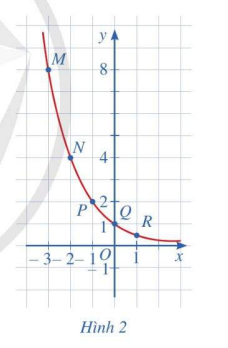
c) Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) với trục tung và vị trí của đồ thị hàm số đó so với trục hoành.
d) Quan sát đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\), nêu nhận xét về:
- \(\mathop {\lim {{\left( {\frac{1}{2}} \right)}^x}}\limits_{x \to + \infty } ;\,\mathop {\lim {{\left( {\frac{1}{2}} \right)}^x}}\limits_{x \to - \infty } \)
- Sự biến thiên của hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) và lập bảng biến thiên của hàm số đó.
Cho hàm số mũ \(y = {2^x}\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.
Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{2^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {2^x}\) (Hình 1)
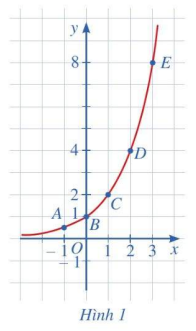
c) Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {2^x}\) với trục tung và vị trí của đồ thị hàm số đó so với trục hoành.
d) Quan sát đồ thị hàm số \(y = {2^x}\), nêu nhận xét về:
- \(\mathop {\lim {2^x}}\limits_{x \to + \infty } ;\,\mathop {\lim {2^x}}\limits_{x \to - \infty } \)
- Sự biến thiên của hàm số \(y = {2^x}\) và lập bảng biến thiên của hàm số đó.
Xét bài toán ở phần mở đầu.
a) Tính số tiền doanh nghiệp đó có được sau 1 năm, 2 năm, 3 năm.
b) Dự đoán công thức tính số tiền doanh nghiệp đó có được sau n năm.
Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\). Từ đó, hãy tìm x sao cho \({\left( {\frac{1}{2}} \right)^x} > 2\).

Điều kiện xác định của \({x^{ - 3}}\) là
A. \(x \in \mathbb{R}\)
B. \(x \ge 0\)
C. \(x \ne 0\)
D. \(x > 0\)
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ \(y = {a^x};\,y = {b^x};\,y = {c^x}\) được cho bởi Hình 14. Kết luận nào sau đây là đúng đối với ba số a, b, c ?
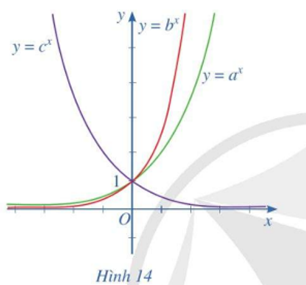
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Vẽ đồ thị của các hàm số mũ sau:
a) \(y = {(\sqrt 3 )^x}\);
b) \(y = {\left( {\frac{1}{4}} \right)^x}\).
Trong các hàm số sau, hàm số nào đồng biến?
A. \(y = {\left( {\frac{{\sqrt 3 }}{2}} \right)^x}\).
B. \(y = {\left( {\frac{e}{3}} \right)^x}\).
C. \(y = {\left( {\frac{\pi }{2}} \right)^x}\).
D. \(y = {\left( {\frac{3}{\pi }} \right)^x}\).
Nếu một ô kính ngăn khoảng \(3{\rm{\% }}\) ánh sáng truyền qua nó thì phần trăm ánh sáng \(\rho \) truyền qua \(n\) ô kính liên tiếp được cho gần đúng bởi hàm số sau:
\(p\left( n \right) = 100 \cdot {(0,97)^n}{\rm{.\;}}\)
a) Có bao nhiêu phần trăm ánh sáng sẽ truyền qua 10 ô kính?
b) Có bao nhiêu phần trăm ánh sáng sẽ truyền qua 25 ô kính? (Kết quả ở câu a và câu b đựơc làm tròn đến hàng đơn vị).
Hàm số \(y = {\rm{ln}}\left( {{x^2} - 2mx + 1} \right)\) có tập xác định là \(\mathbb{R}\) khi
A. \(m = 1\).
B. \(m > 1\) hoặc \(m < - 1\).
C. \(m < 1\).
D. \( - 1 < m < 1\).
Tập xác định của hàm số \(y = 0,{2^{x - 1}}\) là:
A. \(\mathbb{R}\backslash \left\{ 1 \right\}.\)
B. \(\mathbb{R}.\)
C. \(\left( {1; + \infty } \right).\)
D. \(\left( {0; + \infty } \right).\)
Trong các hàm số sau, hàm số nghịch biến trên tập xác định của nó là:
A. \(y = {e^x}.\)
B. \(y = {\left( {\frac{1}{5}} \right)^x}.\)
C. \(y = {\left( {\sqrt 5 } \right)^x}.\)
D. \(y = {\left( {1,2} \right)^x}.\)







Danh sách bình luận