Độ lớn \(M\) (theo độ Richter) của một trận động đất được xác định như Hoạt động mở đầu.
a) Tìm độ lớn theo thang Richter của các trận động đất có biên độ lớn nhất lần lượt là \({10^{3,5}}\mu m;100000\mu m;{100.10^{4,3}}\mu m\).
b) Một trận động đất có biên độ lớn nhất \(A = 65000\mu m\) thì độ lớn \(M\) của nó phải thoả mãn hệ thức nào?
Sử dụng công thức đo biên độ lớn nhất của một trận động đất là \(A = {10^M}\mu m\).
a) Với \(A = {10^{3,5}}\mu m\) thì \(M = 3,5\).
Với \(A = 100000\mu m = 1{0^5}\mu m\) thì \(M = 5\).
Với \(A = {100.10^{4,3}}\mu m = {10^2}{.10^{4,3}}\mu m = {10^{6,3}}\mu m\) thì \(M = 6,3\).
a) Với \(A = 65000\mu m\) ta có: \({10^M} = 65000\).

Các bài tập cùng chuyên đề
Tính:
a) \({\log _3}3\sqrt 3 ;\)
b) \({\log _{\frac{1}{2}}}32.\)
Tìm x, biết:
a) \({2^x} = 8;\)
b) \({2^x} = \frac{1}{4};\)
c) \({2^x} = \sqrt 2 .\)
Tính đạo hàm của hảm số \(y = {x^{10}}\) tại \(x = - 1\) và \(x = \sqrt[3]{2}\).
Tính:
a) \({\log _3}\sqrt[3]{3}\);
b) \({\log _{\frac{1}{2}}}8\);
c) \({\left( {\frac{1}{{25}}} \right)^{{{\log }_5}4}}\).
Cho các số thực dương \(a,M,N\) với \(a \ne 1\). Bạn Quân đã vẽ sơ đồ và tìm ra công thức biến đổi biểu thức \({\log _a}\left( {MN} \right)\) như sau:
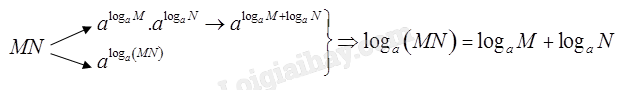
a) Giải thích cách làm của bạn Quân.
b) Vẽ sơ đồ tương tự để tìm công thức biến đổi cho \({\log _a}\frac{M}{N}\) và \({\log _a}{M^\alpha }\left( {\alpha \in \mathbb{R}} \right)\).
Tính giá trị các biểu thức sau:
a) \({\log _2}16\);
b) \({\log _3}\frac{1}{{27}}\);
c) \(\log 1000\);
d) \({9^{{{\log }_3}12}}\).
Nếu \({a^{\frac{1}{2}}} = b\left( {a > 0,a \ne 1} \right)\) thì
A. \({\log _{\frac{1}{2}}}a = b\).
B. \(2{\log _a}b = 1\).
C. \({\log _a}\frac{1}{2} = b\).
D. \({\log _{\frac{1}{2}}}b = a\).
Tính
a) \({\log _4}\sqrt[5]{{16}}\).
b) \({36^{{{\log }_6}8}}\).
Cho \(a > 0;a \ne 1\). Tình:
a) \({\log _a}1\)
b) \({\log _a}a\)
c) \({\log _a}{a^c}\)
d) \({a^{{{\log }_a}b}}\,\,\,(b > 0)\)
Tính
a) \({\log _3}81\).
b) \({\log _{10}}\frac{1}{{100}}\).







Danh sách bình luận