Một hộp sữa tươi có dạng hình hộp chữ nhật với dung tích 1 lít, chiều cao 20 cm, chiều dài 10 cm
a) Tính chiều rộng của hộp sữa.
b) Tính diện tích vật liệu dùng để làm vỏ hộp sữa ? ( coi như phần mép hộp không đáng kể).

a)\(V = a.b.h \Rightarrow b = \frac{V}{{a.h}}\)
b) Diện tích vật liệu = diện tích xung quanh + tổng 2 diện tích đáy.
Đổi : 1 lít = 1 \(d{m^3}\) = 1000 \(c{m^3}\)
a)
Chiều rộng của hộp sữa là:
1000: (20 . 10) = 1000 : 200= 5 (cm)
b)
Diện tích vật liệu dùng để làm vỏ hộp sữa là diện tích xung quanh và diện tích của hai mặt đáy của hình hộp.
Diện tích xung quanh của hộp sữa là:
\(\left( {10 + 5} \right).2.20 = 600\left( {c{m^2}} \right)\)
Diện tích của hai mặt đáy là:
\(2.10.5 = 100\left( {c{m^2}} \right)\)
Vậy diện tích vật liệu cần dùng là:
\(600 + 100 = 700\left( {c{m^2}} \right)\)

Các bài tập cùng chuyên đề
Một viên gạch đất sét nung đặc có dạng hình hộp chữ nhật với các kích thước của đáy dưới là 220 mm, 105 mm và chiều cao là 65 mm. Tính diện tích xung quanh và thể tích của viên gạch đó.
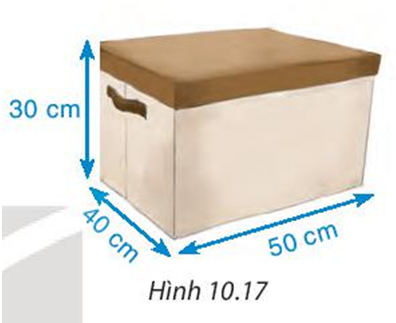
Một chiếc hộp đựng đồ đa năng có dạng hình hộp chữ nhật với khung bằng thép, bên ngoài phủ vải và kích thước như hình 10.17
a) Tính thể tích của hộp.
b) Tính diện tích vải phủ bề mặt ngoài của chiếc hộp.
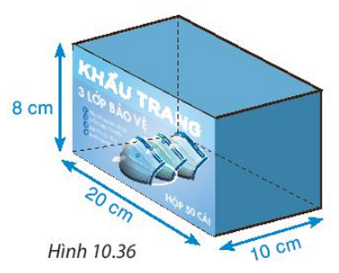
Một hộp đựng khẩu trang y tế được làm bằng bìa cứng có dạng một hình hộp chữ nhật, kích thước như hình 10.36.
a) Hãy tính thể tích của hộp.
b) Tính diện tích bìa cứng dùng để làm hộp (bỏ qua mép dán).
Người ta làm một cái hộp có dạng hình hộp chữ nhật bằng bìa với chiều dài 20 cm, chiều rộng 14 cm và chiều cao 15 cm.
a) Tích thể tích của cái hộp.
b) Tính diện tích bìa dùng để làm cái hộp.
Một bể cá dạng hình hộp chữ nhật làm bằng kính (không có nắp) có chiều dài 80 cm, chiều rộng 50 cm, chiều cao 45 cm. Mực nước ban đầu trong bể cao 35 cm.
a) Tính diện tích kính dùng để làm bể cá đó
b) Người ta cho vào bể một hòn đá trang trí chìm hẳn trong nước thì mực nước của bể dâng lên thành 37,5 cm. Tính thể tích hòn đá.
Một xưởng sản xuất đồ nội thất muốn sản xuất tủ quần áo có kích thước như hình vẽ.
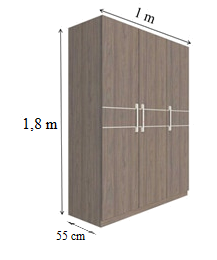
Diện tích gỗ xưởng cần dùng để làm một chiếc tủ như thiết kế đó (giả sử độ dày của gỗ không đáng kể) là:
-
A.
\(5,4\,m^2\);
-
B.
\(5,9\,m^2\);
-
C.
\(6,4\,m^2\);
-
D.
\(6,9\,m^2\).
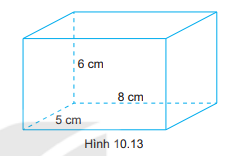
Cho hình hộp chữ nhật có kích thước như Hình 10.13. Tính thể tích, diện tích xung quanh của hình hộp chữ nhật.
Một hộp sữa tươi có dạng hình hộp chữ nhật với dung tích 1 lít, chiều cao 20cm, chiều dài 10cm.
a) Tính chiều rộng của hộp sữa.
b) Coi diện tích vật liệu dùng để làm vỏ hộp sữa? (Coi như phần mép hộp không đáng kể).

Một chiếc hộp đựng đồ đa năng có dạng hình hộp chữ nhật với khung bằng thép, bên ngoài phủ vải và có kích thước như Hình 10.7.
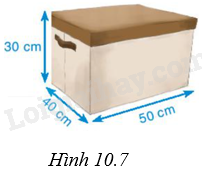
a) Tính thể tích của hộp.
b) Tính diện tích vải phủ bề mặt ngoài của chiếc hộp.
Người ta làm một cái hộp có dạng hình hộp chữ nhật bằng bìa với chiều dài 20cm, chiều rộng 14cm và chiều cao 15cm.
a) Tính thể tích của cái hộp.
b) Tính diện tích bìa dùng để làm cái hộp.
Một bể cá dạng hình hộp chữ nhật làm bằng kính (không có nắp) có chiều dài 80cm, chiều rộng 50cm, chiều cao 45cm. Mực nước ban đầu trong bể cao 35cm.
a) Tính diện tích kính dùng để làm bể cá đó.
b) Người ta cho vào bể một hòn đá trang trí chìm hẳn trong nước thì mực nước của bể dâng lên thành 37,5cm. Tính thể tích hòn đá.







Danh sách bình luận