Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.
\(At\parallel BC\)
\(\widehat {ABC} = \widehat {BAt}\)(Hai góc so le trong)
\(\widehat {ACB} = \widehat {MAt}\)(Hai góc đồng vị)
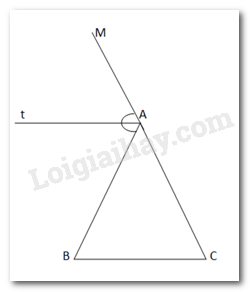
Gọi AM là tia đối của AC. At là đường phân giác của \(\widehat {MAB} \Rightarrow \widehat {MAt} = \widehat {BAt}\)
Ta có: \(At\parallel BC\) nên:
\(\widehat {ABC} = \widehat {BAt}\)(Hai góc so le trong)
\(\widehat {ACB} = \widehat {MAt}\)(Hai góc đồng vị)
Mà \(\widehat {MAt} = \widehat {BAt}\)\( \Rightarrow \widehat {ABC} = \widehat {ACB}\)
Vậy tam giác ABC cân tại A ( Dấu hiệu nhận biết tam giác cân).

Các bài tập cùng chuyên đề
Mỗi tam giác có mấy đường phân giác?
Cắt một tam giác bằng giấy. Hãy gấp tam giác vừa cắt để được ba đường phân giác của nó. Mở tờ giấy ra, hãy quan sát và cho biết ba nếp gấp đó có cùng đi qua một điểm không (H.9.33)
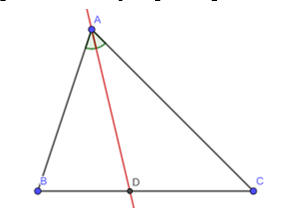
Vẽ và cắt hình tam giác ABC rồi gấp hình sao cho cạnh AB trùng với cạnh AC ta được nếp gấp AD (Hình 1). Đoạn thẳng AD nằm trên tia phân giác của góc nào của tam giác ABC ?
Trong Hình 3, hãy vẽ các đường phân giác GM, EN và FP của tam giác EFG.
Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.
a) Chứng minh rằng tam giác MBE cân.
b) Chứng minh rằng \(\widehat {EBH} = \widehat {ACM}\)
c) Chứng minh rằng \(EB \bot BC\)
Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D (Hình 110). Các đầu mút của đoạn thẳng AD có đặc điểm gì?
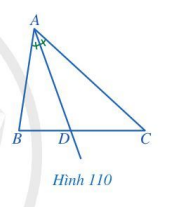
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung tuyến của tam giác đó.
Tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh:
a) \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \);
b) \(\widehat {BIC} = 90^\circ + \dfrac{1}{2}\widehat {BAC}\).
Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.
a) Chứng minh \(\widehat {CBI} > \widehat {ACI}\);
b) So sánh IB và IC.
a) Gọi I là giao điểm của hai đường phân giác BE và CF của tam giác ABC. Đường thẳng qua I song song với BC cắt AB tại J và cắt AC tại K. Chứng minh: JK = BJ + CK.
b) Đường thẳng qua B vuông góc với BI cắt đường thẳng qua C vuông góc với CI tại điểm I’. Qua I’ kẻ đường thẳng song song với BC cắt AB tại J’, cắt AC tại K’. Chứng minh J’K’ = BJ’ + CK’.
Tam giác ABC có số đo ba góc thoả mãn: \(\widehat A = \widehat B + \widehat C\). Hai tia phân giác của góc A và góc B cắt nhau tại điểm I. Khi đó góc BIC có số đo là:
A. \({120^0}\)
B. \({125^0}\)
C. \({130^0}\)
D. \({135^0}\)
Xét tam giác ABC vuông tại A; đường phân giác góc B cắt cạnh AC tại E; đường thẳng qua E vuông góc với BC cắt đường thẳng AB tại K. Chứng minh:
a) AE < EC
b) BK = BC.
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Gọi H và K là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh rằng DH = DK.
Cho tam giác ABC có M là giao điểm của hai đường phân giác của góc B và góc C. Cho biết \(\widehat {BMC} = {132^o}\). Tính số đo các góc \(\widehat {MAB}\) và \(\widehat {MAC}\).
Cho tam giác ABC có \(\widehat {ABC} + \widehat {ACB} = 2\widehat {BAC}\). Hai tia phân giác của góc B và góc C cắt nhau tại K. Trong các phát biểu sau, phát biểu nào sai?
a) Số đo góc KAC bằng 30°.
b) Số đo góc BAK bằng 25°.
c) Số đo góc BKC bằng 120°.
d) Số đo góc BKC bằng 115°.
Cho tam giác ABC vuông tại C có \(\widehat{CAB}=60^\circ\), AE là tia phân giác của góc CAB (E ∈ BC). Gọi D là hình chiếu của B trên tia AE, K là hình chiếu của E trên AB. Chứng minh:
a) EB là tia phân giác của góc DEK, EK là tia phân giác của góc BEA;
b) EC = ED = EK.
Cho tam giác ABC vuông tại A có góc B bằng \({60^o}\). Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC \(\left( {M \in BC} \right)\).
a) Chứng minh \(\Delta ABE = \Delta MBE\).
b) Chứng minh \(MB = MC\).
c) Gọi I là giao điểm của BA và ME. Chứng minh \(IE > EM\).
Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của tia AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.
A. \(\widehat {BOC} = {120^\circ }\).
B. \(\widehat {BAO} = \dfrac{1}{2}\widehat {BAC}\).
C. \(\widehat {BOC} = {160^\circ }\).
D. \(\widehat {BAO} < {30^\circ }\).







Danh sách bình luận