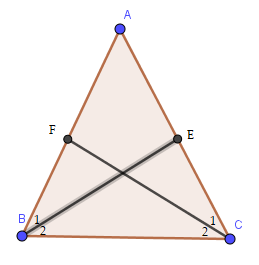
Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.
Sử dụng tính chất của tam giác cân, xét 2 tam giác bằng nhau rồi chỉ ra 2 cạnh tương ứng bằng nhau.
Vì tam giác ABC cân tại A nên AB = AC; \(\widehat {ABC} = \widehat {ACB}\) ( tính chất)
Vì BE là là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì CF là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Do đó, \(\widehat {{B_1}} = \widehat {{C_1}}\)
Xét \(\Delta ABE\) và \(\Delta ACF\), ta có:
\(\widehat A\) chung
AB = AC
\(\widehat {{B_1}} = \widehat {{C_1}}\)
\( \Rightarrow \Delta ABE = \Delta ACF\left( {g.c.g} \right)\)
\( \Rightarrow \)BE = CF ( 2 cạnh tương ứng)

Các bài tập cùng chuyên đề
Điểm cách đều ba cạnh của tam giác là:
-
A.
Giao điểm của ba đường cao
-
B.
Giao điểm của ba đường trung trực
-
C.
Giao điểm của ba đường trung tuyến
-
D.
Giao điểm của ba đường phân giác
Cho tam giác ABC có hai đường phân giác AM, BN cắt nhau tại điểm I. Hỏi CI có là đường phân giác của góc C không?
Chứng minh rằng trong tam giác đều, điểm cách đều 3 cạnh của tam giác là trọng tâm của tam giác đó.
Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC bằng 120\(^\circ \).
Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB.
a) Hãy giải thích tại sao DP = DR.
b) Hãy giải thích tại sao DP = DQ.
c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A? ( Đây là một cách chứng minh định lí 2)
Vẽ một tam giác trên giấy. Cắt rời tam giác ra khỏi tờ giấy rồi gấp hình tam giác đó để xác định ba đường phân giác của tam giác (Hình 4). Em hãy quan sát và nhận xét xem ba đường phân giác có cùng đi qua một điểm không.
Một nông trại nằm trên mảnh đất hình tam giác có ba cạnh tường rào tiếp giáp với ba con đường (Hình 7). Hỏi phải đặt trạm qua sát ở đâu để nó cách đều ba cạnh tường rào?
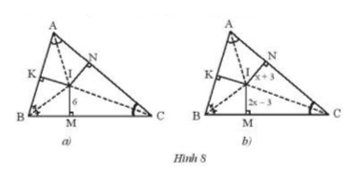
Trong Hình 8, I là giao điểm của ba đường phân giác của tam giác ABC.
a) Cho biết IM = 6 (Hình 8a). Tính IK và IN.
b) Cho biết IN = x + 3, IM = 2x – 3 (Hình 8b). Tìm x
Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C.
Cho tam giác ABC cân tại A. Tia phân giác của các góc B và C cắt nhau tại M. Tia AM cắt BC tại H. Chứng minh rằng H là trung điểm của BC
Cho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thằng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN.
Cho tam giác AMN vuông tại A. Tia phân giác của góc M và N cắt nhau tại I. Tia MI cắt AN tại R. Kẻ RT vuông góc với AI tại T. Chứng minh rằng AT = RT.
Ba thành phố A, B, C được nối với nhau bởi xa lộ (Hình 9). Người ta muốn tìm một địa điểm để làm một sân bay sao cho địa điểm này phải cách đều ba xa lộ đó. Hãy xác định vị trí của sân bay thỏa mãn điều kiện trên và giải thích cách thực hiện.
Cho tam giác ABC vuông tại A có AB = \(\dfrac{1}{2}\)AC, AD là tia phân giác \(\widehat {BAC}\)(D ∈ BC). Gọi E là trung điểm của AC.
a) Chứng minh rằng DE = DB
b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.
c) AD cắt CK tại H. Chứng minh rằng AH\( \bot \)KC.
Bạn Ngân gấp một miếng bìa hình tam giác để các nếp gấp tạo thành ba tia phân giác của các góc ở đỉnh của tam giác đó (Hình 109).
Ba nếp gấp đó có đặc điểm gì?
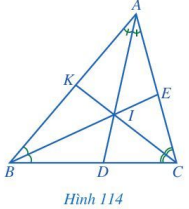
Quan sát các đường phân giác AD, BE, CK của tam giác ABC (Hình 114), cho biết ba đường phân giác đó có cùng đi qua một điểm hay không.
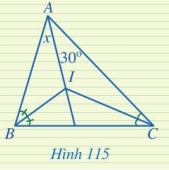
Tìm số đo x trong Hình 115.
Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.
Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.
a) Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao?
b) Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?
Cho tam giác ABC cân tại A có \(\widehat {ABC} = 70^\circ \). Hai đường cao BD và CE cắt nhau tại H.
a) Tính số đo các góc còn lại của tam giác ABC.
b) Chứng minh BD = CE.
c) Chứng minh tia AH là tia phân giác của góc BAC.
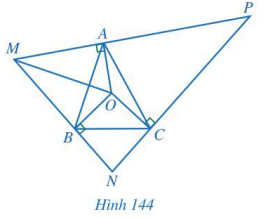
Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144). Chứng minh:
a) \(\Delta OMA = \Delta OMB\) và tia MO là tia phân giác của góc NMP;
b) O là giao điểm của ba đường phân giác của tam giác MNP.
Tam giác ABC có AD, BE là hai đường phân giác và \(\widehat {BAC} = {120^0}\). Chứng minh rằng DE là tia phân giác của góc ADC.
Cho tam giác ABC có \(\widehat {{A^{}}} = {42^o}\), ba đường phân giác đồng quy tại I. Tính số đo góc BIC.
Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác. Chứng minh tam giác ABC là tam giác cân.
Cho tam giác ABC có M là điểm đồng quy của ba đường phân giác. Qua M vẽ đường thẳng song song với Bc và cắt AB, AC lần lượt tại N và P. Chứng minh rằng
NP = BN + CP.
Cho tam giác ABC có ba đường phân giác AD, BE, CF đồng quy tại I. Vẽ IH vuông góc với BC tại H. Chứng minh rằng \(\widehat {BIH} = \widehat {CI{\rm{D}}}\).
Cho tam giác ABC (AB < AC). Trên tia phân giác của góc A, lấy điểm E nằm trong tam giác ABC sao cho E cách đều hai cạnh AB, BC. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Điểm E không nằm trên tia phân giác của góc B.
b) \(\widehat {EBC} = \widehat {ECB}\).
c) Điểm E cách đều AB, BC, CA.
d) Điểm E nằm trên tia phân giác của góc C.
Cho tam giác ABC cân tại A có K là trung điểm của đoạn BC. Hai đường phân giác BD và CE cắt nhau tại I. Chứng minh:
a) I cách đều ba cạnh của tam giác ABC;
b) KI là tia phân giác của góc EKD.
Cho hai đường thẳng song song a, b và một đường thẳng c (c cắt a tại E, c cắt b tại F). Hai tia phân giác của các góc aEF và bFE cắt nhau tại I. Gọi A, B lần lượt là hình chiếu của I trên các đường thẳng a và b (Hình 52).
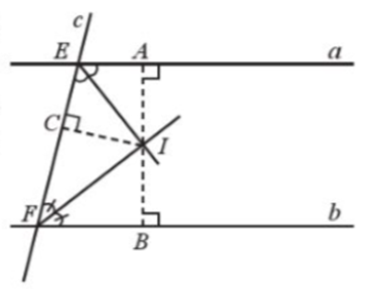
Chứng minh:
a) Tam giác EIF là tam giác vuông;
b) IA = IB.
Cho tam giác ABC cân tại A có M là trung điểm của BC. G là giao điểm của hai trung tuyến BD và CE.
a) Chứng minh: GA, GM, MA lần lượt là tia phân giác của các góc DGE, BGC, EMD.
b) Tìm điều kiện của tam giác ABC để EG là tia phân giác của góc DEM.







Danh sách bình luận