Cho tam giác ABC nội tiếp trong đường tròn (O). Gọi H là trực tâm tam giác ABC và B’ là điểm đối xứng với B qua tâm O . Hãy so sánh các vectơ \(\overrightarrow {AH} \) và \(\overrightarrow {B'C} ,\overrightarrow {AB'} \) và \(\overrightarrow {HC} \).
Ta có B’ là điểm đối xứng với B qua tâm O nên BB’ là đường kính, suy ra \(\widehat {B'CB} = 90^\circ \Rightarrow B'C \bot BC\) và \(\widehat {B'AB} = 90^\circ \Rightarrow B'A \bot BA\)
Mặt khác ta có: \(AH \bot BC,CH \bot AB\), suy ra \(B'C//AH,AB'//CH\).
Suy ra AB’CH là hình bình hành.
Vậy \(\overrightarrow {AH} = \overrightarrow {B'C} \) và \(\overrightarrow {AB'} = \overrightarrow {HC} \).
Các bài tập cùng chuyên đề
Trong các điều kiện dưới đây, chọn điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B,
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
Cho hình thang cân ABCD với hai đáy AB, CD, \(AB < CD\). Hãy chỉ ra mối quan hệ về độ dài, phương, hướng giữa các cặp vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \), \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \). Có cặp vectơ nào trong các cặp vectơ trên bằng nhau hay không?
Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi \(\overrightarrow {BC} = \overrightarrow {AD}.\)
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập hợp S gồm tất cả các vecto khác \(\overrightarrow 0 \). Hãy chỉ ra tập hợp S gồm tất cả các vceto khác \(\overrightarrow 0 \), có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
Thế nào là hai lực cân bằng? Nếu dùng hai vectơ để biểu diễn hai lực cần bằng thì hai vectơ này có mối quan hệ gì với nhau?
Cho tam giác ABC. Vẽ điểm D thỏa mãn \(\overrightarrow {AD} = \overrightarrow {BC} .\) Tứ giác ABCD là hình gì?
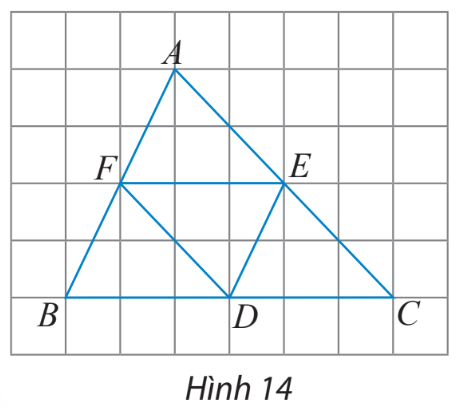
Quan sát hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ở hình 42.
a) Nhận xét về phương của hai vectơ đó.
b) Nhận xét về hướng của hai vectơ đó.
c) So sánh độ dài của hai vectơ đó.
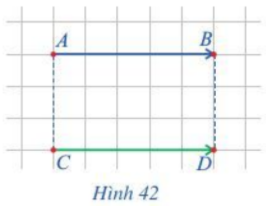
Trong Hình 54, hai ròng rọc có trục quay nằm ngang và song song với nhau, hai vật có trọng lượng bằng nahu. Mỗi dây có một đầu buộc vào vật, một đầu buộc vào một mảnh nhựa cứng. Hai vật lần lượt tác động lên mảng nhựa các lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} .\) Nhận xét về hướng và độ dài của mỗi cặp vecto sau:
a) \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{P_2}} \) biểu diễn trọng lực của hai vật
b) \(\overrightarrow {{F_1}} \) và \(\;\overrightarrow {{F_2}} .\)
(Bỏ qua trọng lượng các dây và các lực ma sát).
Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn. Tìm điều kiện cần và đủ để hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau.
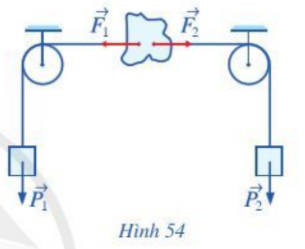
Cho D, E, F lần lượt là trung điểm của cạnh BC, CA, AB của tam giác ABC (hình 14).
a) Tìm các vectơ bằng vectơ \(\overrightarrow {EF} \).
b) Tìm các vectơ đối vectơ \(\overrightarrow {EC} \).
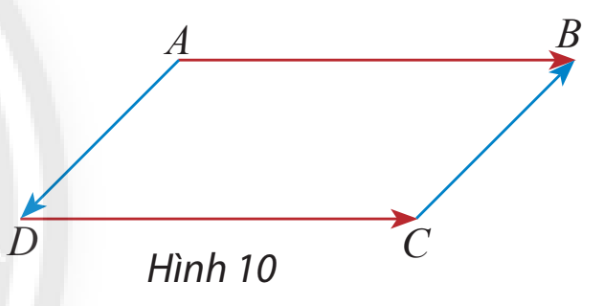
Cho hình bình hành ABCD (hình 30), hãy so sánh độ dài và hướng của hai vectơ :
a) \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \)
b) \(\overrightarrow {AD} \) và \(\overrightarrow {CB} \)
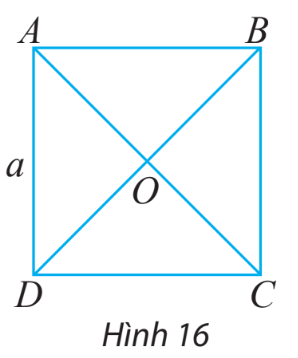
Cho hình vuông ABCD có tâm O và có các cạnh bằng a (hình 16)
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\)
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \)
Cho hình bình hành \(ABCD\) tâm \(O\). Gọi \(K,\,\,L,\,\,M,\,\,N\) tướng ứng là trung điểm các cạnh \(AB,\,\,BC,\,\,CD,\,\,DA.\) Trong các vectơ có đầu mút lấy từ các điểm \(A,\,\,B,\,\,C,\,\,D,\,\,K,\)\(L,\,\,M,\,\,O\) có bao nhiêu vectơ bằng vectơ \(\overrightarrow {AK} \)?
A. 2
B. 6
C. 4
D. 8
Cho hình bình hành \(ABCD\) tâm \(O.\) Gọi \(M,\,\,N\) theo thứ tự là trung điểm của \(BC,\,\,AD.\) Gọi \(I,\,\,J\) lần lượt là giao điểm của \(BD\) với \(AM,\,\,CN.\) Xét các cevtơ khác \(\overrightarrow 0 ,\) các đầu mút lấy từ các điểm \(A,\,\,B,\,\,C,\,\,D,\,\,M,\,\,N,\,\,I,\,\,J,\,\,O.\)
a) Hãy chỉ ra những vectơ bằng vectơ \(\overrightarrow {AB} ;\) những vectơ cùng hướng với \(\overrightarrow {AB} .\)
b) Chứng minh rằng \(BI = IJ = JD.\)
Trong mặt phẳng cho hai điểm phân biệt A, B. Tập hợp tất cả các điểm M thỏa mãn \(\left| {\overrightarrow {AM} } \right| = \left| {\overrightarrow {AB} } \right|\) là hình gì?
A. Đường trung trực của đoạn thẳng AB
B. Đường tròn tâm A bán kính AB
C. Đường tròn tâm B bán kính AB
D. Đoạn thẳng AB
Cho \(\overrightarrow a = \overrightarrow b \). Phát biểu nào sau đây là sai?
A. \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng
B. \(\overrightarrow a \) và \(\overrightarrow b \) cùng độ dài
C. \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương
D. \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Cho điểm I là trung điểm của đoạn thẳng AB. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {IA} = \overrightarrow {IB} \)
B. \(\overrightarrow {IA} \) và \(\overrightarrow {IB} \) cùng hướng
C. \(\overrightarrow {AI} = \overrightarrow {BI} \)
D. \(\overrightarrow {AI} = \overrightarrow {IB} \)
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng:
a) \(\overrightarrow {MN} = \overrightarrow {PA} \).
b) \(\overrightarrow {MP} = \overrightarrow {CN} \).
Cho hình thoi ABCD cạnh bằng a và có tâm O, góc \(\widehat {BAD} = 60^\circ \)
a) Tìm trong hình hai vectơ bằng nhau, và có độ dài bằng \(\frac{{a\sqrt 3 }}{2}\)
b) Tìm trong hai hình đối nhau và có độ dài bằng \(a\sqrt 3 \)
Gọi O là tâm của hình bát giác đều ABCDEFGH
a) Tìm hai vectơ khác \(\overrightarrow 0 \) và cùng hướng với \(\overrightarrow {OA} \)
b) Tìm vt bằng vt \(\overrightarrow {BD} \)
Cho lục giác đều ABCDEF có tâm O. Số các vectơ bằng vectơ \(\overrightarrow {OC} \) có điểm đầu và điểm cuối la các đỉnh của lục giác là:
A. 2
B. 3
C. 4
D. 6
Tìm các cặp số thực a và b sao cho mỗi cặp vecto sau bằng nhau:
a) \(\overrightarrow u = \left( {2a - 1; - 3} \right)\) và \(\overrightarrow v = \left( {3;4b + 1} \right)\).
b) \(\overrightarrow x = \left( {a + b; - 2a + 3b} \right)\) và \(\overrightarrow y = \left( {2a - 3;4b} \right)\).
