Một hình chóp đều và một hình lăng trụ đứng có diện tích đáy bằng nhau. Chiều cao của hình chóp đều gấp đôi chiều cao của hình lăng trụ đứng. Thể tích của hình chóp đều là

Quan sát các hình không gian trong Hình 1 và trả lời các câu hỏi sau:

a) Các mặt bên của mỗi hình là hình gì?

b) Hình nào có các cạnh bên bằng nhau và đáy là hình tam giác đều?

c) Hình nào có các cạnh bên bằng nhau và đáy là hình vuông?

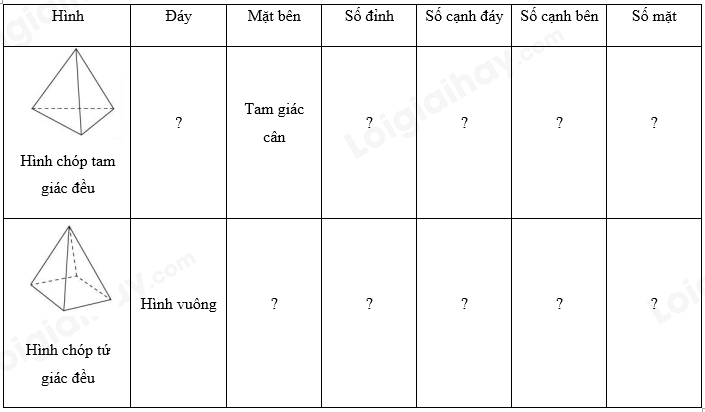
Quan sát hai hình dưới đây và thay mỗi dấu ? cho thích hợp.

Các phát biểu sau đúng hay sai? Nếu sai thì sửa lại cho đúng.

a) Hình chóp tam giác đều có các cạnh bên bằng nhau và đáy là hình tam giác có ba cạnh bằng nhau.

b) Hình chóp tứ giác đều có tất cả các cạnh bằng nhau.

Hãy giải bài toán ở phần mở đầu (trang 49)

a) Bạn Mai cần dán giấy bóng kính màu xung quanh một chiếc lồng đèn hình chóp tam giác đều với kích thước như hình bên. Hỏi diện tích giấy mà Mai cần là bao nhiêu?

b) Bạn Hùng dùng một cái gàu hình chóp tứ giác đều để múc nước đổ vào một thùng chứa hình lăng trụ có cùng diện tích đáy và chiều cao như hình bên. Hãy dự đoán xem bạn Hùng phải đổ bào nhiêu gàu thì nước đầy thùng.

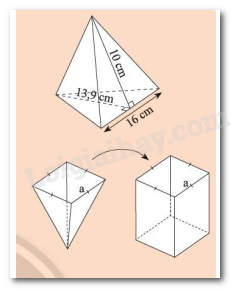
a) Tính diện tích xung quanh của hình chóp tam giác đều có độ dài cạnh đáy là \(10\)cm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tam giác đều là \(12\)cm.

b) Tính diện tích toàn phần và thể tích của hình chóp tứ giác đều có độ dài cạnh đáy là \(72\)dm, chiều cao là \(68,1\)dm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều là \(77\)dm.

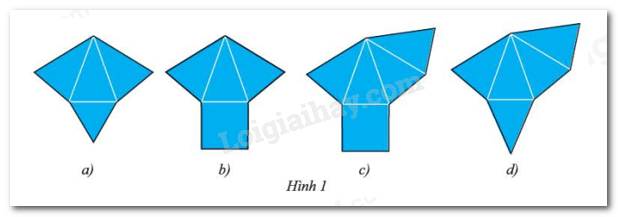
Trong các tấm bìa ở Hình 1, tấm bìa nào gấp được hình chóp tam giác đều, tấm bìa nào gấp được hình chóp tứ giác đều?

Quan sát Hình 4, Hình 14 và tìm số thích hợp cho ? trong các bảng sau:

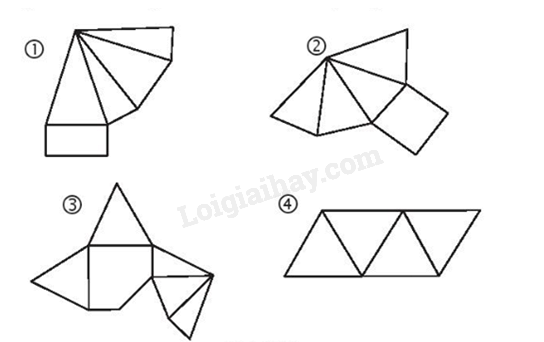
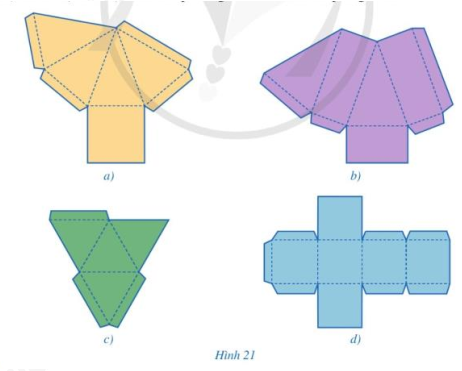
Trong các miếng bìa ở hình 21a, 21b, 21c, 21d, miếng bìa nào có thể gấp (theo các nét đứt) và dán lại để được hình chóp tam giác đều? Hình chóp tứ giác đều?

Xét tính đúng sai của các phát biểu sau đây:

a)     Diện tích xung quanh của hình chóp tam giác đều bằng ba lần diện tích mỗi mặt bên;

b)    Diện tích xung quanh của hình chóp tam giác đều bằng tích của chu vi đáy với đường cao của mặt bên kẻ từ đỉnh của nó;

c)     Diện tích xung quanh của hình chóp tứ giác đều bằng tổng diện tích của tất cả các mặt bên.

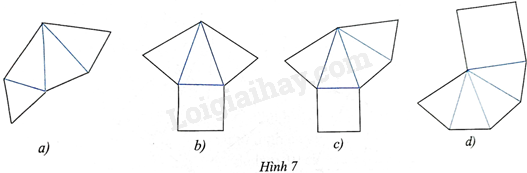
Trong các hình khai triển sau, hình nào gấp theo đường màu xanh thì được một hình chóp tam giác đều hay một hình chóp tứ giác đều.

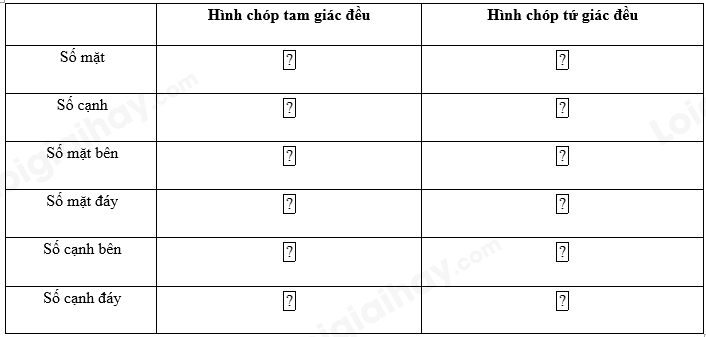
Hoàn thành bảng sau:

Trong các miếng bìa sau, miếng bìa nào gấp được hình chóp tam giác đều, hình chóp tứ giác đều? 

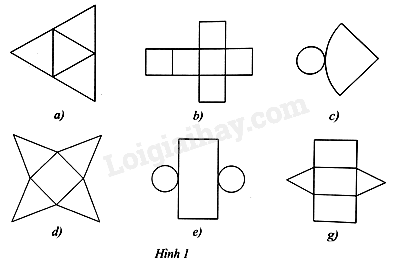
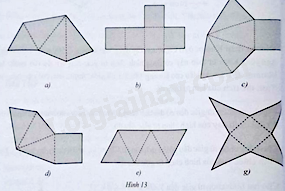
Trong những miếng bìa ở các hình 13a, 13b, 13c, 13d,13e, 13g, miếng bìa nào không gấp lại (theo các nét nứt) để được hình chóp tam giác đều hoặc hình chóp tứ giác đều?

Trong các miếng bìa ở Hình 10.32, miếng bìa nào khi gấp và dán lại thì được một hình chóp tam giác đều, miếng nào được hình chóp tứ giác đều.

Gọi tên đỉnh, cạnh bên, cạnh đáy, đường cao và một trung đoạn của hình chóp tam giác đều, hình chóp tứ giác đều.

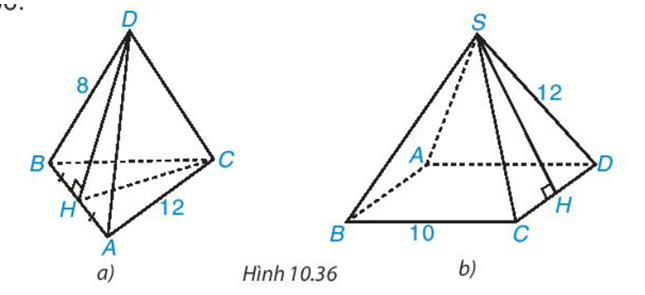
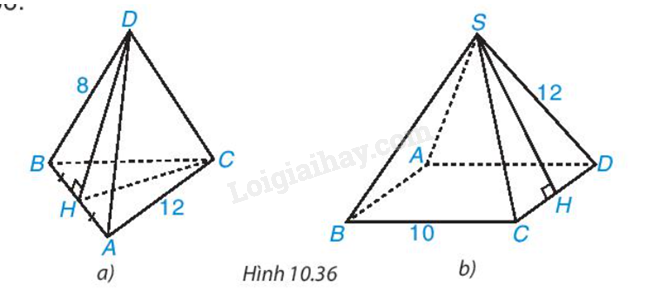
Tính diện tích xung quanh của hình chóp tam giác đều, hình chóp tứ giác đều trong Hình 10.36

Hình chóp tam giác đều và hình chóp tứ giác đều có chung đặc điểm nào sau đây?

1. Chiếc hộp (Hình a) được vẽ lại như Hình b có dạng hình chóp tam giác đều S.MNP.

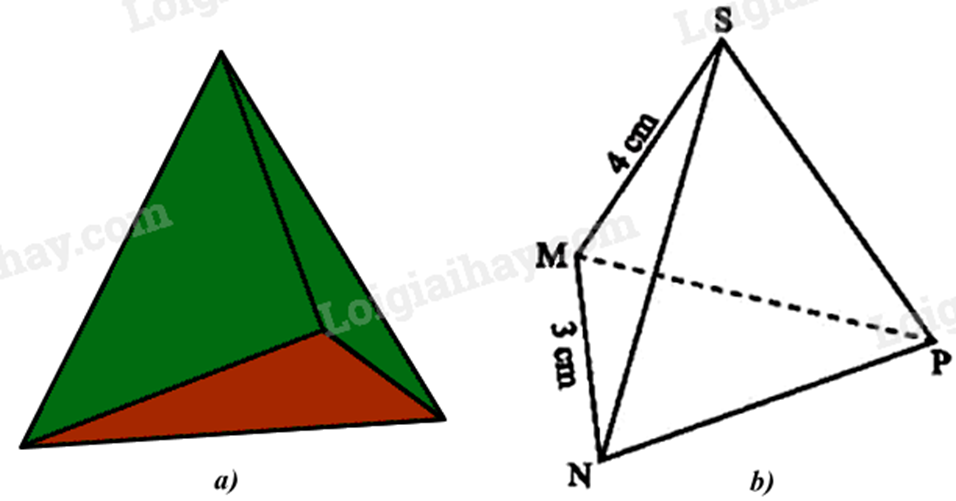
a) Hãy cho biết mặt đáy, mặt bên, cạnh bên của chiếc hộp đó.

b) Cho biết SM = 4cm, MN = 3 cm. Tìm độ dài các cạnh còn lại của chiếc hộp.

2. Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.

a) Cạnh bên của hình chóp là bao nhiêu?

b) Tính thể tích hình chóp.