Cho hàm số \(y = f\left( x \right) = 2\left( {x + 1} \right)\left( {x - 3} \right) + 2x - 6\). Giá trị của hàm số khi x = 3 là:

A. 8 

B. 0

C. -6   

D. 3

Để xây dựng phương án kinh doanh cho một loại sản phẩm, doanh nghiệp tính toán lợi nhuận y (đồng) theo công thức sau: \(y =  - 200{x^2} + 92{\rm{ }}000x - 8{\rm{ }}400{\rm{ }}000\), trong đó x là số sản phẩm loại đó được bán ra.

a) Với mỗi giá trị x = 100, x = 200, tính giá trị tương ứng của y.

b) Với mỗi giá trị của x có bao nhiêu giá trị tương ứng của y?

Trong bài toán ở phần mở đầu, ta đã biết công thức tính quãng đường đi được \(S\left( m \right)\) của vật rơi tự do theo thời gian \(t\left( s \right)\) là: \(S = \frac{1}{2}g{t^2}\), trong đó \(g\) là gia tốc rơi tự do, \(g \approx 9,8\left( {m/{s^2}} \right)\).

a) Với mỗi giá trị \(t = 1,t = 2\), tính giá trị tương ứng của S.

b) Với mỗi giá trị của t có bao nhiêu giá trị tương ứng của S?

Bảng 1 dưới đây cho biết chỉ số \(P{M_{2,5}}\) (bụi mịn) ở thành phố Hà Nội từ tháng 1 đến tháng 12 của năm 2019.

(Nguồn: Báo cáo chất lượng không khí thế giới 2019)

a) Nêu chỉ số \(P{M_{2,5}}\) trong tháng 2; tháng 5; tháng 10.

b) Chỉ số \(P{M_{2,5}}\) có phải là hàm số của tháng không? Tại sao?

Galileo Galilei (1564 - 1642). sinh tại thành phố Pisa (Italia). là nhà bác học vī đại của thời kì Phục Hưng. Ông được mệnh danh là “cha đẻ của khoa học hiện đại”. Trước Galileo. người ta tin rằng vật nặng rơi nhanh hơn vật nhẹ, ông đã bác bỏ điểu này bằng thí nghiệm nổi tiếng ở tháp nghiêng Pisa. Từ thí nghiệm của Galileo, các nhà khoa học sau này được truyển cảm hứng rằng chúng ta chỉ có thể rút ra tri thúc khoa học từ các quy luật khách quan của tự nhiên, chứ không phải từ niềm tin.

Làm thế nào để mô tả được mối liên hệ giữa thời gian t và quãng đuờmg đi đuợc S của vật rơi tự do? Làm thế nào để có được hình ảnh hình học mình hoạ mối liên hệ giữa hai đại lượng đó?

Bản tin dự báo thời tiết cho biết nhiệt độ ở một số thời điểm trong ngày 01/5/2021 tại thành phố Hồ Chí Minh đã được ghi lại thành bảng kèm với biểu đồ bên.

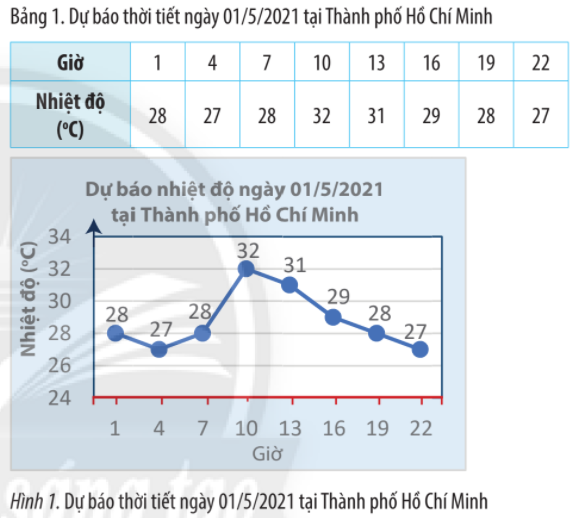
Sử dụng bảng hoặc biểu đồ, hãy:

a) Viết tập hợp các mốc đã có dự báo nhiệt độ.

b) Viết tập hợp các số đo nhiệt độ đã dự báo.

c) Cho biết nhiệt độ dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021.

Số 2 đã trải qua một hành trình thú vị và bị biến đổi sau khi đi qua chiếc hộp đen

Bác thợ máy đã giải mã hộp đen cho một số x bất kì như sau:

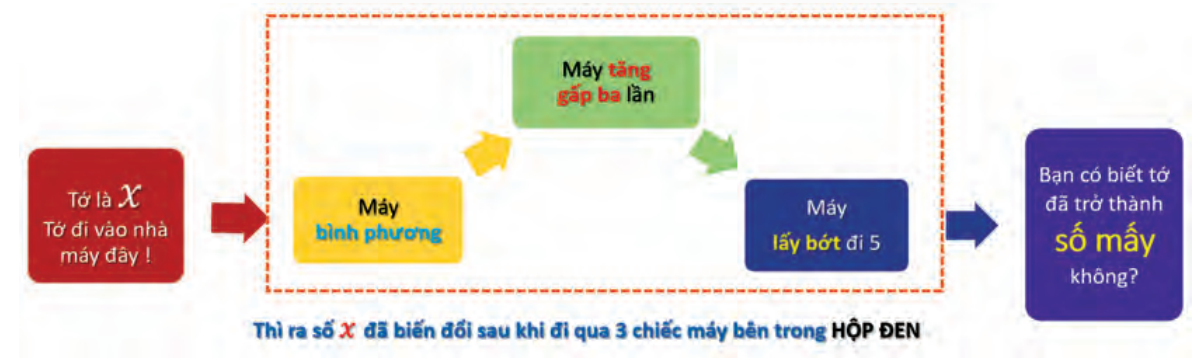
Bên trong HỘP ĐEN là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết iểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.

Trong các công thức sau, công thức nào không biểu diễn \(y\) là hàm số của \(x\)?

A. \(x + 2y = 3\)

B. \(y = \sqrt {{x^2} - 2x} \)

C. \(y = \frac{1}{x}\)

D. \({x^2} + {y^2} = 4\)

a) Dựa vào bảng 6.2 về già bán lẻ điện sinh hoạt, hãy tính số tiền phải trả ứng với mỗi lượng điện tiêu thụ ở Bảng 6.3:

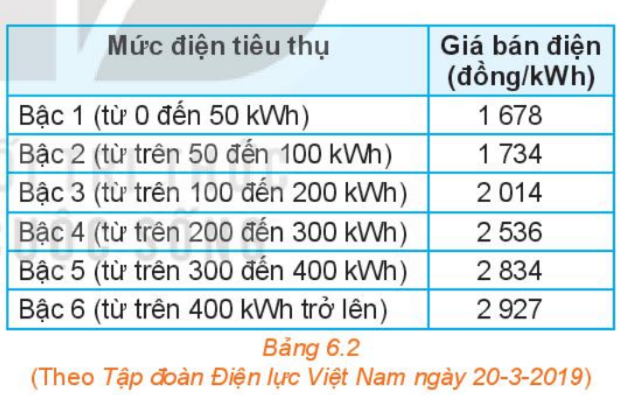
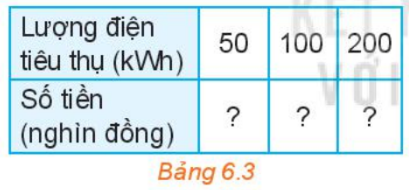
b) Gọi x là lượng điện tiêu thụ (đơn vị kWh) và y là số tiền phải trả tương ứng (đơn vị nghìn đồng). Hãy viết công thức mô tả sự phụ thuộc của y vào x khi \(0 \le x \le 50\).

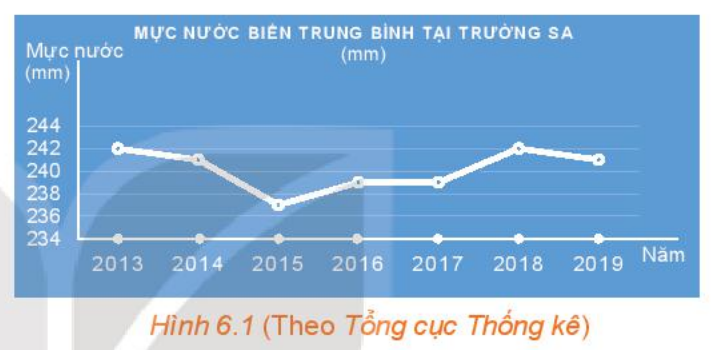
Quan sát Hình 6.1.

a) Thời gian theo dõi mực nước biển ở Trường Sa được thể hiện trong hình từ năm nào đến năm nào?

b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại Trường Sa cao nhất, thấp nhất?

Bảng 6.1 cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong ngày 25-3-2021 tại một trạm quan trắc ở thủ đô Hà Nội:

a) Hãy cho biết nồng độ bụi PM 2.5 tại mỗi thời điểm 8 giờ, 12 giờ, 16 giờ.

b) Trong Bảng 6.1, mỗi thời điểm tương ứng với bao nhiêu giá trị của nồng độ bụi PM 2.5?

Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là hàm số của x?

a) \(x + y = 1\)

b) \(y = {x^2}\)

c) \({y^2} = x\)            

d) \({x^2} - {y^2} = 0\)

Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là một hàm số của x?

a) \({x^2} + y = 4\)

b) \(4x + 2y = 6\)   

c) \(x + {y^2} = 4\)   

d) \(x - {y^3} = 0\)

Các đường dưới đây, đường nào không là đồ thị hàm số?