Cho tam giác \(ABC.\) Gọi \(D,\,\,E,\,\,F\) theo thứ tự là trung điểm của các cạnh \(BC,\,\,CA,\,\,AB.\)
a) Xác định vectơ \(\overrightarrow {AF} - \overrightarrow {BD} + \overrightarrow {CE} \)
b) Xác định điểm \(M\) thỏa mãn \(\overrightarrow {AF} - \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {MA} .\)
c) Chứng minh rằng \(\overrightarrow {MC} = \overrightarrow {AB} .\)
- Chứng minh \(\overrightarrow {AF} = \overrightarrow {FB} ,\) \(\overrightarrow {BD} = \overrightarrow {DC} \)
- Áp dụng quy tắc hình bình hành với hai vectơ \(\overrightarrow {CE} \) và \(\overrightarrow {CD} \)
- Chứng minh tứ giác \(ABCM\) là hình bình hành
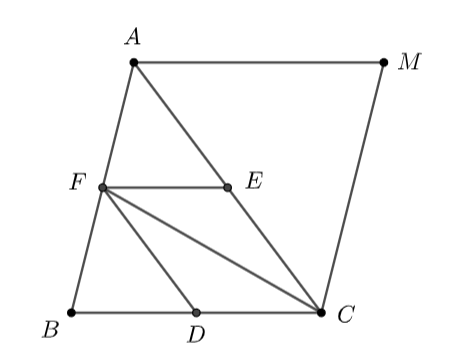
a) Ta có: \(DF\) là đường trung bình của \(\Delta ABC\)
\( \Rightarrow \) \(\overrightarrow {CE} = \overrightarrow {DF} \)
\( \Rightarrow \) tứ giác \(CDFE\) là hình bình hành.
Ta có: \(D\) và \(F\) lần lượt là trung điểm của \(BC\) và \(AB\)
\( \Rightarrow \) \(\overrightarrow {AF} = \overrightarrow {FB} ,\) \(\overrightarrow {BD} = \overrightarrow {DC} \)
Ta có: \(\overrightarrow {AF} - \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {AF} + \overrightarrow {CD} + \overrightarrow {CE} = \overrightarrow {AF} + \overrightarrow {CF} = \overrightarrow {CF} + \overrightarrow {FB} = \overrightarrow {CB} \)
b) Theo câu a, ta có: \(\overrightarrow {AF} - \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {CB} \)
mặt khác \(\overrightarrow {AF} - \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {MA} .\)
nên \(\overrightarrow {CB} = \overrightarrow {MA} \)
\( \Rightarrow \) tứ giác \(ABCM\) là hình bình hành
\( \Rightarrow \) \(M\) là điểm đối xứng với \(B\) qua \(E\)
c) Theo câu b, ta có: tứ giác \(ABCM\) là hình bình hành
\( \Rightarrow \) \(\overrightarrow {MC} = \overrightarrow {AB} .\)

Các bài tập cùng chuyên đề
Cho bốn điểm \(A, B, C, D\). Chứng minh rằng:
a) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \)
b) \(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BC} - \overrightarrow {BD} \)
Cho hình bình hành ABCD. Hãy tìm điểm M để \(\overrightarrow {BM} = \overrightarrow {AB} + \overrightarrow {AD} \). Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {CD} \) và \(\overrightarrow {CM} \).
Cho tam giác đều ABC có cạnh bằng a. Tính độ dài của các vectơ \(\overrightarrow {AB} - \overrightarrow {AC} ,\;\overrightarrow {AB} + \overrightarrow {AC} .\)
Hình 4.19 biểu diễn hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động lên một vật, cho \(\left| {\overrightarrow {{F_1}} } \right| = 3\;N,\;\left| {\overrightarrow {{F_2}} } \right| = 2\;N.\) Tính độ lớn của hợp lực \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \).
Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng không khổi và có độ lớn bàng nhau. Hai tàu luôn dược giữ lái sao cho chúng tạo với bờ cùng một góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc dòng nước là đáng kể, các yêu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước.
Cho hình vuông ABCD có cạnh a. Tính độ dài của các vectơ sau:
a) ;
b) ;
c) với O là giao điểm của AC và BD.
Cho hình vuông ABCD có cạnh a. Tính độ dài các vecto sau:
a) \(\overrightarrow {DA} + \overrightarrow {DC} \)
b) \(\overrightarrow {AB} - \overrightarrow {AD} \)
c) \(\overrightarrow {OA} + \overrightarrow {OB} \) với O là giao điểm của AC và BD.
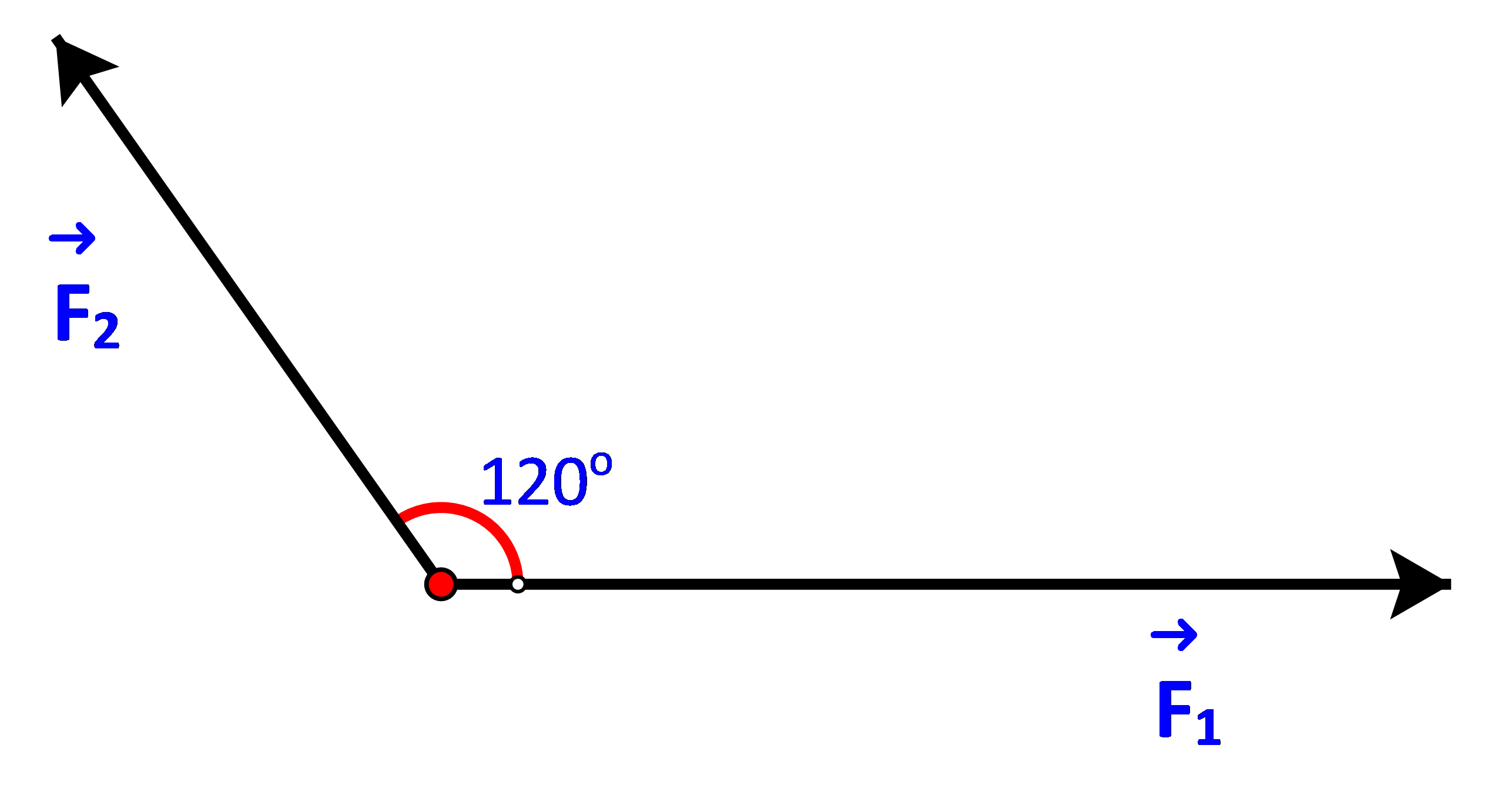
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB} \) và \(\overrightarrow {{F_3}} = \overrightarrow {OC} \) cùng tác động vào một vật tại điểm O và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} \)đều là 120 N và \(\widehat {AOB} = {120^o}\). Tìm cường độ và hướng của lực \(\overrightarrow {{F_3}} .\)
Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc là 10 km/h. Một chiếc ca nô chuyển động từ phía đông sang phía tây với vận tốc 40 km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông.
Chứng minh:
a) Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {CE} = \overrightarrow {AE} \) với E là điểm bất kì.
b) Nếu I là trung điểm của đoạn thẳng AB thì \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {IN} = 2\overrightarrow {MN} \) với M, N là hai điểm bất kì.
c) Nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} - 3\overrightarrow {MN} = 3\overrightarrow {NG} \) với M, N là hai điểm bất kì.
Cho hình bình hành ABCD có O là giao điểm hai đường chéo và một điểm M tùy ý. Chứng minh rằng:
a) \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0;} \)
b) \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \)
Cho tứ giác ABCD, thực hiện cả phép cộng và trừ vectơ sau:
a) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA}\);
b) \(\overrightarrow {AB} - \overrightarrow {AD} \)
c) \(\overrightarrow {CB} - \overrightarrow {CD} \).
Cho tam giác đều ABC cạnh bằng a. Tính độ dài các vectơ:
a) \(\overrightarrow {BA} + \overrightarrow {AC} \);
b) \(\overrightarrow {AB} + \overrightarrow {AC} \);
c) \(\overrightarrow {BA} - \overrightarrow {BC} \).
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Chứng minh rằng:
a) \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {OD} - \overrightarrow {OC;} \)
b) \(\overrightarrow {OA} - \overrightarrow {OB} + \overrightarrow {DC} = \overrightarrow 0 \)
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} \)và \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều là 10 N và \(\widehat {AMB} = 90^\circ \) Tìm độ lớn của lực \(\overrightarrow {{F_3}} \).
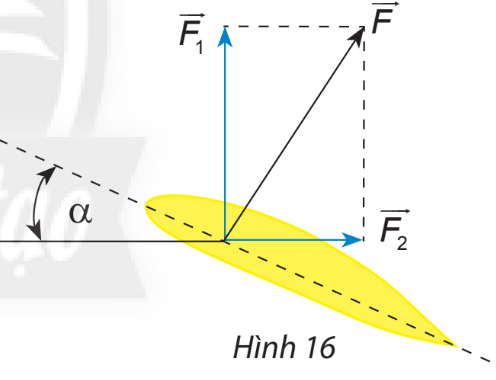
Khi máy bay nghiêng cánh một góc \(\alpha \), lực \(\overrightarrow F \) của không khí tác động vuông góc với cánh và bằng tổng của lực nâng \(\overrightarrow {{F_1}} \) và lực cản \(\overrightarrow {{F_2}} \) (Hình 16). Cho biết \(\alpha = 30^\circ \)và \(\left| {\overrightarrow F } \right| = a\). Tính \(\left| {\overrightarrow {{F_1}} } \right|\) và \(\left| {\overrightarrow {{F_2}} } \right|\) theo a.
Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn \(\overrightarrow {KA} + \overrightarrow {KC} = \overrightarrow 0 ;\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 ;\overrightarrow {HA} + \overrightarrow {HD} + \overrightarrow {HC} = \overrightarrow 0 \). Tính độ dài các vectơ \(\overrightarrow {KA} ,\overrightarrow {GH} ,\overrightarrow {AG} \).
Một con tàu có vectơ vận tốc chỉ theo hướng nam, vận tốc của dòng nước là một vectơ theo hướng đông như hình 17. Tính độ dài vectơ tổng của hai vectơ nói trên.
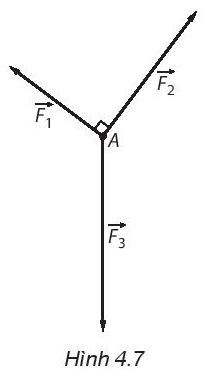
Trên Hình 4.7 biểu diễn ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) cùng tác động vào một vị trí cân bằng \(A.\) Cho biết \(\left| {\overrightarrow {{F_1}} } \right| = 30N,\,\,\left| {\overrightarrow {{F_2}} } \right| = 40N.\) Tính cường độ của lực \(\overrightarrow {{F_3}} .\)
Trên mặt phẳng, chất điểm \(A\) chịu tác động của ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) và ở trạng thái cân bằng. Góc giữa hai vectơ \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} \) bằng \({60^ \circ }.\) Tính độ lớn của \(\overrightarrow {{F_3}} ,\) biết rằng \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = 2\sqrt 3 N.\)
Một vật đồng chất được thả vào một cốc chất lỏng. Ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng. Tìm mối liên hệ giữa trọng lực \(\overrightarrow P \) cuẩ vật và lực đẩy Archimedes \(\overrightarrow F \) mà chất lỏng tác động lên vật. Tìm tỉ số giữa trọng lượng riêng của vật và của chất lỏng.
Cho tam giác \(ABC.\) Tập hợp các điểm \(M\) thỏa mãn \(\left| {\overrightarrow {MC} - \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} - \overrightarrow {AC} } \right|\) là:
A. Đường tròn tâm \(A\) bán kính \(BC\)
B. Đường thẳng đi qua \(A\) và song song với \(BC\)
C. Đường tròn đường kính \(BC\)
D. Đường thẳng đi qua \(A\) và vuông góc với \(BC\)
Cho tam giác ABC vuông tại A, \(AB = 4a,AC = 5a\). Tính
a) \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\).
b) \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).
Cho tam giác ABC thỏa mãn \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\) (*). Chứng minh tam giác ABC vuông tại A.
Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Chứng minh rằng nếu hai vectơ cùng hướng thì \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\).
Cho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\).
Cho tam giác ABC. Tìm tập hợp các điểm M trong mặt phẳng thỏa mãn \(\left| {\overrightarrow {AB} + \overrightarrow {BM} } \right| = \left| {\overrightarrow {AC} - \overrightarrow {AM} } \right|\).
Cho hai tam giác ABC và A’B’C’ có cùng trọng tâm là G. Chứng minh \(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = \overrightarrow 0 \).
Cho tam giác nhọn ABC có các cạnh đôi một khác nhau. Gọi H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp của tam giác, D là điểm đối xứng với H qua O. Chứng minh \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \).
Cho tam giác đều ABC cạnh a. Tính:
a) \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right|\)
b) \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\)
c) \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\)








Danh sách bình luận