Hình 108 minh họa mặt cắt đứng của tủ sách nghệ thuật nhà bác Ngọc. Sau một thời gian sử dụng, tủ sách đó đã có dấu hiệu bị xuống cấp và cần sửa lại. Các tấm ngăn BM, CN, DP bị hỏng và cần thay mới. Em hãy giúp bác Ngọc tính toán chiều dài các tấm ngăn mới lần lượt thay thế cho các tấm ngăn BM, CN, DP đã bị hỏng. Biết chiều dài tấm ngăn EQ bằng 4m.
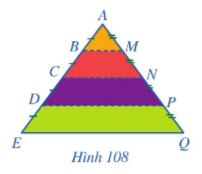
Sử dụng định lý Thales để tìm ra độ dài các cạnh BM, CN, DP.
Theo định lý Thales ta có:
\(BM\parallel EQ \Rightarrow \frac{{BM}}{{EQ}} = \frac{{AB}}{{AE}} \Rightarrow \frac{{BM}}{4} = \frac{1}{4} \Rightarrow BM = 1\)
\(CN\parallel EQ \Rightarrow \frac{{CN}}{{EQ}} = \frac{{AC}}{{AE}} \Rightarrow \frac{{CN}}{4} = \frac{2}{4} \Rightarrow CN = 2\)
\(DP\parallel EQ \Rightarrow \frac{{DP}}{{EQ}} = \frac{{AD}}{{AE}} \Rightarrow \frac{{DP}}{4} = \frac{3}{4} \Rightarrow DP = 3\)
Vậy bác Ngọc cần chuẩn bị các miếng ván BM 1m, CN 2m, DP 3m.

Các bài tập cùng chuyên đề
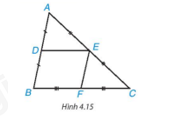
Cho DE là đường trung bình của tam giác ABC (H.4.15)
Sử dụng định lí Thalès đảo, chứng minh rằng DE // BC.
Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?
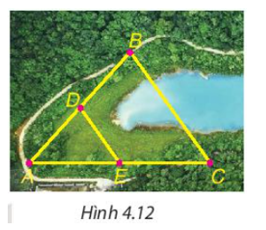
Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
Cho DE là đường trung bình của tam giác ABC (H.4.15)
Gọi F là trung điểm của BC. Chứng minh tứ giác DEFB là hình bình hành. Từ đó suy ra DE = \(\frac{1}{2}\)BC
Tính các độ dài x, y trong Hình 4.18.
Cho tam giác ABC có trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E.
a) Chứng minh DC // EM.
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM.
Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng
A. 3,5 cm.
B. 7 cm.
C. 10 cm.
D. 15 cm.
Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là
A. 8 cm.
B. 64 cm.
C. 30 cm.
D. 16 cm.
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành.
Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.32. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.
Tìm độ dài x, y trong hình vẽ dưới đây:
Cho tam giác DEF. Gọi H, K, I lần lượt là các trung điểm của DE, DF và EF. Chứng minh rằng tứ giác HKIE là hình bình hành.
Cho tam giác ABC, các đường trung tuyến BD, CE cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng \(EI = DK\)
Cho hình chữ nhật ABCD. Gọi D’, E, F, G lần lượt là trung điểm các cạnh AB, BC, CD, DA. Tứ giác D’EFG là hình gì? Vì sao?
Cho tam giác ABC có \(BC = 13cm.\) E và F lần lượt là trung điểm của AB, AC. Độ dài EF bằng:
A. 13cm
B. 26cm
C. 6,5cm
D. 3cm
Cho tam giác ABC cân tại B. Hai trung tuyến AM, BN cắt nhau tại G. Gọi I và K lần lượt là trung điểm của GB, GC. Khẳng định nào đúng?
A. \(MN = \frac{1}{2}AC\)
B. \(BC = \frac{1}{2}IK\)
C. \(MN > IK\)
D. \(MN = IK\)
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Biết \(AG = 4cm\), độ dài của EI, DK là
A. \(EI = DK = 3cm\)
B. \(EI = 3cm,DK = 2cm\)
C. \(EI = DK = 2cm\)
D. \(EI = 1cm,DK = 2cm\)
Cho \(\Delta ABC\) đều, cạnh 3cm; M, N lần lượt là trung điểm AB, AC. Chu vi của tứ giác MNCB bằng
A. 8cm
B. 7,5cm
C. 6cm
D. 7cm
Cho tam giác ABC có \(AB = 6cm,AC = 8cm,BC = 10cm.\) Gọi H, I, K lần lượt là trung điểm của AB, BC, AC. Chu vi tứ giác AHIK bằng:
A. 7cm
B. 14cm
C. 24cm
D. 12cm
Tìm độ dài x trong Hình 4.10.
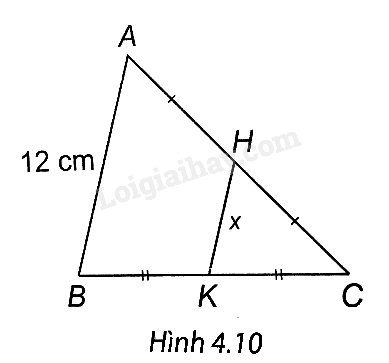
A. 12 cm.
B. 24 cm.
C. 6 cm.
D. 10 cm.
Quan sát Hình 4.11 và chọn khẳng định đúng.

A. DE = NP.
B. DF = 2MP.
C. EF = 2DM.
D. NP = 2DE.
Cho tam giác ABC có chu vi bằng 20 cm. Gọi M, N, P lần lượt là trung điểm của AB, BC, AC. Chu vi tam giác MNP bằng:
A. 20 cm.
B. 10 cm2.
C. 10 cm.
D. 40 cm.
Cho ∆ABC đều, cạnh 3 cm; M, N là trung điểm của AB và AC. Chu vi của tứ giác MNCB bằng:
A. 8 cm.
B. 7,5 cm.
C. 6 cm.
D. 7 cm.
Tính các độ dài x, y trong Hình 4.12
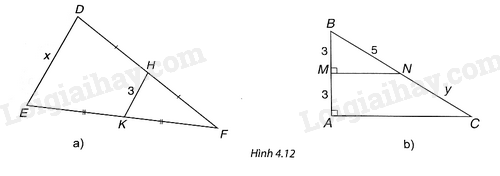
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh tứ giác BMNC là hình thang.
b) Tứ giác MNPB là hình gì? Tại sao?
Cho tam giác ABC, trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E.
a) Chứng minh: DC // EM.
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM.
Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh tứ giác AHOK là hình chữ nhật.
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng EI = DK.
Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.
a) Chứng minh EK // CD, FK // AB.
b) So sánh EF và \(\frac{1}{2}\left( {AB + CD} \right).\)
Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng
A. 3,5 cm.
B. 7 cm.
C. 10 cm.
D. 15 cm.









Danh sách bình luận