Trong Hình 64, chứng minh tam giác \(CDM\) vuông tại \(M\).
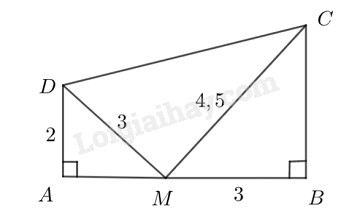
Hình 64
- Chứng minh \(\Delta ADM \backsim\Delta BMC\)
- Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\)
- Dựa vào tính chất tổng hai góc nhọn trong tam giác vuông bằng \(90^\circ \) ta chứng minh \(\widehat {AMD} + \widehat {BMC} = 90^\circ \)
- Suy ra \(\widehat {DMC} = 90^\circ \) hay tam giác \(CDM\) vuông tại \(M\).
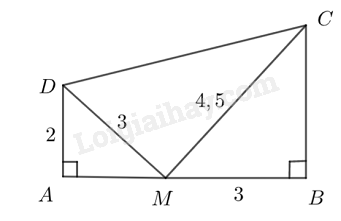
Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\) nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có \(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\) vuông tại \(M\).

Các bài tập cùng chuyên đề
Cho hai hình chữ nhật ABCD và A’B’C’D’ thỏa mãn \(AC = 3AB,B'D' = 3A'B'\)
Nếu \(AB = 2A'B'\) và diện tích hình chữ nhật ABCD là \(12{m^2}\) thì diện tích hình chữ nhật A’B’C’D’ là bao nhiêu?
-
A.
\(6{m^2}\)
-
B.
\(8{m^2}\)
-
C.
\(10{m^2}\)
-
D.
\(3{m^2}\)
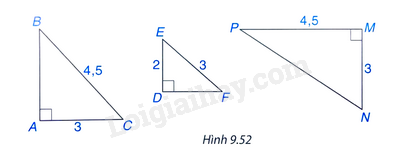
Hãy chỉ ra các cặp tam giác vuông đồng dạng với nhau trong Hình 9.52, viết đúng kí hiệu đồng dạng.
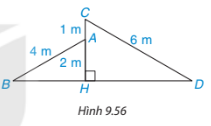
Một ngôi nhà với hai mái lệch AB, CD được thiết kế như Hình 9.56 sao cho CD=6m, AB=4m, HA=2m, AC=1m. Chứng tỏ \(\widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\).
Bác Minh muốn thay chiếc ti vi có chiều ngang của màn hình là 72cm (loại 32 inch) bằng chiếc ti vi mới loại 55 inch có cùng tỉ lệ khung hình (tỉ lệ giữa hai kích thước màn hình). Hỏi nếu khoảng trống đặt ti vi là một hình vuông cạnh 1m thì có thể đặt chiếc tivi mới vào đó không? (Biết rằng 1 inch = 2,54m).
Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn AC=3AB, B′D′=3A′B′
a) Chứng minh rằng tam giác ABC đồng dạng với tam giác A'B'C'
b) Nếu A'B' = 2AB và diện tích hình chữ nhật ABCD là 2m2 thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu
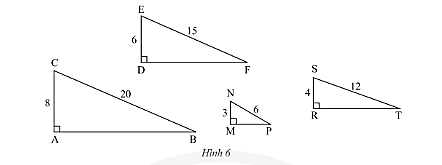
Trong Hình 6, tam giác nào đồng dạng với tam giác \(DEF\)?
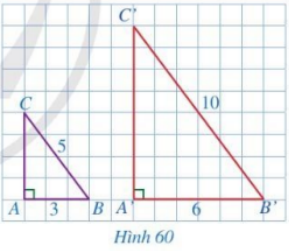
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ (Hình 60) sao cho \(AB = 3,\,\,BC = 5,\,\,A'B' = 6,\,\,B'C' = 10\).
a) Tính CA và C’A’
b) So sánh các tỉ số \(\frac{{A'B'}}{{AB}};\,\,\frac{{A'C'}}{{AC}};\,\,\frac{{B'C'}}{{BC}}\)
c) Hai tam giác A’B’C’ và ABC có đồng dạng với nhau hay không?
Đối với hai tam giác vuông \(ABC\) và \(A'B'C'\) trong hình 6.82, em hãy cho biết:
1. Cặp cạnh \(AB,BC\) và \(A'B',B'C'\) có tỉ lệ với nhau không?
2. Độ dài các cạnh \(AC\) và \(A'C'\) là bao nhiêu và vì sao hai tam giác vuông này đồng dạng?

Chỉ ra các cặp tam giác vuông đồng dạng với nhau trong Hình 6.84.

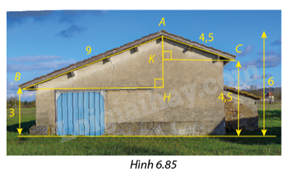
Góc nghiêng \(\widehat {ABH}\) của mép mái nhà bên trái so với phương ngang và góc nghiêng \(\widehat {ACK}\) của mép mái nhà bên phải so với phương ngang trong Hình 6.85 có bằng nhau không? Vì sao?
Cho tứ giác ABCD như Hình 9.11. Biết rằng \(\widehat {BAD} = \widehat {BDC} = {90^0},AD = 4cm,BD = 6cm\) và \(BC = 9cm.\) Chứng minh rằng BC//AD.
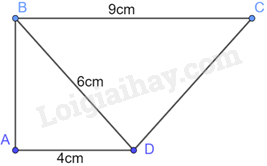
Hình 9.11
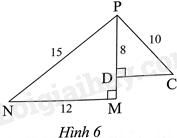
Quan sát Hình 6, chứng minh rằng:
a) $\Delta MNP\backsim \Delta DPC$.
b) $NP\bot PC$.
Cho tam giác \(IKH\) và tam giác \(I'K'H'\) có \(\widehat {IKH} = 90^\circ ,\widehat {KHI} = 60^\circ ,\widehat {I'K'H'} = 90^\circ ,\widehat {K'I'H'} = 30^\circ \). Chứng minh: \(\Delta I'K'H'\backsim \Delta IKH\).
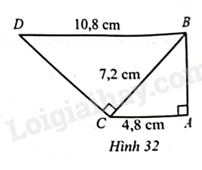
Quan sát Hình 32 có \(\widehat {BAC} = 90^\circ ,\widehat {BCD} = 90^\circ ,DB = 10,8\)cm, \(BC = 7,2\)cm và \(CA = 4,8\)cm. Chứng minh: \(\Delta DBC\backsim \Delta BCA\).
Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn AC = 3AB, B′D′ = 3A′B′.
a) Chứng minh rằng tam giác ABC đồng dạng với tam giác A'B'C'
b) Nếu A'B' = 2AB và diện tích hình chữ nhật ABCD là 2m2 thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu
Cho \(\Delta ABC\) và \(\Delta MNP\) có: \(\widehat A = \widehat M = 90^\circ \). Để kết luận $\Delta ABC\backsim \Delta MNP$ theo trường hợp cạnh huyền – cạnh góc vuông thì cần có thêm điều kiện nào sau đây
-
A.
\(\widehat B = \widehat N\).
-
B.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\).
-
C.
\(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\).
-
D.
\(\frac{{AB}}{{MN}} = \frac{{BC}}{{MP}}\).
Cho điểm B nằm trên đoạn thẳng AC sao cho \(AB = 6cm,BC = 24cm.\) Vẽ về một phía của AC tia Ax và Cy vuông góc với AC. Trên tia Ax lấy điểm E sao cho \(EB = 10cm,\) trên tia Cy lấy điểm D sao cho \(BD = 30cm.\)
Cho các khẳng định sau:
1. Tam giác EBD là tam giác nhọn.
2. Diện tích tam giác EBD bằng \(150c{m^2}\).
3. Chu vi tam giác EBD bằng 60cm.
Trong các khẳng định trên, có bao nhiêu khẳng định đúng?
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{CH}}{{C'H'}} = \frac{{BC}}{{B'C'}}\). Biết rằng \(\widehat {BAC} = 4\widehat {A'C'B'}.\) Chọn đáp án đúng.
-
A.
\(\widehat {BAC} = {90^0}\)
-
B.
\(\widehat {BAC} = {100^0}\)
-
C.
\(\widehat {BAC} = {120^0}\)
-
D.
\(\widehat {BAC} = {110^0}\)
Cho tam giác ABC cân tại A có chu vi bằng 60cm và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{BC}}{{B'C'}} = \frac{3}{2}\). Chu vi tam giác A’B’C’ là:
-
A.
15cm
-
B.
20cm
-
C.
30cm
-
D.
40cm
Cho hình vẽ:
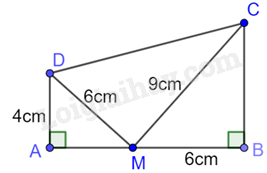
Chu vi tam giác DMC là:
-
A.
\(15 - \sqrt {117} cm\)
-
B.
\(15 + \sqrt {117} cm\)
-
C.
\(15 + \sqrt {118} cm\)
-
D.
\(15 - \sqrt {118} cm\)
Tam giác ABH vuông tại H có \(AB = 25cm,BH = 15cm.\) Trên tia đối của tia HB lấy điểm C sao cho \(AC = \frac{5}{3}AH.\) Chu vi tam giác AHC là:
-
A.
80cm
-
B.
90cm
-
C.
70cm
-
D.
100cm
Cho tam giác ABC vuông tại A, \(AC = 4cm,BC = 6cm.\)Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho \(BD = 9cm.\) Diện tích tam giác ABD bằng:
-
A.
\(9\sqrt {20} c{m^2}\)
-
B.
\(\frac{9}{2}\sqrt {20} c{m^2}\)
-
C.
\(\sqrt {20} c{m^2}\)
-
D.
\(\frac{9}{4}\sqrt {20} c{m^2}\)
Cho tam giác ABC cân tại A, đường cao AH và M là trọng tâm của tam giác ABC; tam giác A’B’C’ cân tại A’, đường cao A’H và M’ là trọng tâm tâm của tam giác A’B’C’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{AB}}{{A'B'}} = 3.\) Chọn đáp án đúng.
-
A.
\(\frac{{BM}}{{B'M'}} = \frac{7}{4}\)
-
B.
\(\frac{{BM}}{{B'M'}} = \frac{5}{2}\)
-
C.
\(\frac{{BM}}{{B'M'}} = \frac{3}{2}\)
-
D.
\(\frac{{BM}}{{B'M'}} = 3\)
Tam giác ABH vuông tại H có \(AB = 20cm,BH = 12cm.\) Trên tia đối của tia HB lấy điểm C sao cho \(AC = \frac{5}{3}AH.\) Khi đó, số đo góc BAC bằng:
-
A.
80\(^0\)
-
B.
90\(^0\)
-
C.
95\(^0\)
-
D.
85\(^0\)
Tam giác ABH vuông tại H có \(AB = 10cm,BH = 6cm.\) Trên tia đối của tia HB lấy điểm C sao cho \(3AC = 5AH.\) Khẳng định nào sau đây là đúng?
-
A.
\(BC = AB + AC\)
-
B.
\(B{C^2} > A{B^2} + A{C^2}\)
-
C.
\(B{C^2} = A{B^2} + A{C^2}\)
-
D.
\(B{C^2} < A{B^2} + A{C^2}\)
Cho tam giác ABC vuông tại A, \(AC = 4cm,BC = 6cm.\) Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho \(BD = 9cm.\) Số đo góc ABD bằng bao nhiêu độ?
-
A.
80\(^0\).
-
B.
90\(^0\).
-
C.
95\(^0\).
-
D.
85\(^0\).
Cho hình vẽ sau:
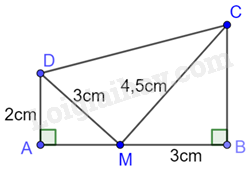
Khẳng định nào sau đây là đúng?
-
A.
\(\widehat {DMC} = {80^0}\)
-
B.
\(\widehat {DMC} = {90^0}\)
-
C.
\(\widehat {DMC} = {100^0}\)
-
D.
\(\widehat {DMC} = {70^0}\)
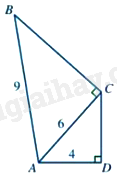
Cho tứ giác ABCD có \(AB = 9cm,\;AC = 6cm,AD = 4,\widehat {ADC} = \widehat {ACB} = {90^0}\) (như hình vẽ)
Khẳng định nào sau đây đúng?
-
A.
\(\widehat {BAC} = \widehat {CAD}\)
-
B.
\(\widehat {BAC} = \frac{2}{3}\widehat {CAD}\)
-
C.
\(\frac{2}{3}\widehat {BAC} = \widehat {CAD}\)
-
D.
\(\widehat {BAC} = \frac{3}{4}\widehat {CAD}\)
Cho hình vẽ:
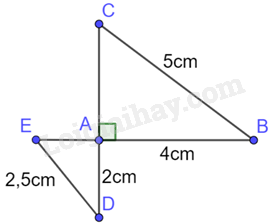
Chọn đáp án đúng.
-
A.
\(\widehat C = \widehat B\)
-
B.
\(\widehat C = \widehat E\)
-
C.
\(\widehat C = \widehat D\)
-
D.
Cả A, B, C đều sai
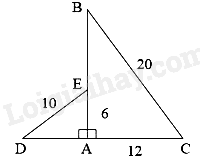
Cho hai tam giác vuông ABC và ADE có các kích thước như hình dưới. Khẳng định nào sau đây đúng?
-
A.
\(\Delta ADE \backsim \Delta BAC\)
-
B.
\(\Delta ADE \backsim \Delta ABC\)
-
C.
\(\Delta ADE \backsim \Delta CBA\)
-
D.
Không có hai tam giác nào đồng dạng với nhau







Danh sách bình luận