Một túi đựng 1 viên bi xanh, 1 viên bi đỏ, 1 viên bi trắng và 1 viên bi vàng có cùng kích thước và khối lượng. Lấy ngẫu nhiên 2 viên bi từ túi. Tính xác suất của các biến cố:
\(A\): “Trong hai viên bi lấy ra có 1 viên bi màu đỏ”;
\(B\): “Hai viên bi lấy ra đều không có màu trắng”.
Khi tất cả các kết quả của một trò chơi hay phép thử ngẫu nghiệm đều có khả năng xảy ra bằng nhau thì xác suất xảy ra biến cố \(A\) là tỉ số giữ số kết quả thuận lời cho \(A\) và tổng số kết quả có thể xảy ra của phép thử, tức là:
\(P\left( A \right) = \)Số kết quả thuận lợi : Số kết quả có thể xảy ra.
a) Cách lấy 2 viên bi trong túi là:
Xanh – đỏ; Xanh – trắng; Xanh – vàng; Đỏ - trắng; Đỏ - vàng; Trắng – vàng.
Có 6 cách lấy hai biên bi từ trong túi.
Biến cố \(A\) xảy ra khi 2 viên bi lấy ra có 1 viên bi màu đỏ
Có 3 kết quả thuận lợi cho biến cố \(A\) là Xanh – đỏ; Đỏ - trắng; Đỏ - vàng
Xác suất 2 viên bi lấy ra có 1 viên bi màu đỏ là \(\frac{3}{6} = \frac{1}{2}\).
Vậy xác suất 2 viên bi lấy ra có 1 viên bi màu đỏ là \(\frac{1}{2}\).
b) Biến cố \(B\) xảy ra khi 2 viên bi lấy ra đều không có màu trắng
Có 3 kết quả thuận lợi cho \(B\) là : Xanh – đỏ; Xanh – vàng; Đỏ - vàng.
Xác suất 2 viên bi lấy ra không có viên bi nào màu trắng là \(\frac{3}{6} = \frac{1}{2}\).
Vậy xác suất 2 viên bi lấy ra không có viên bi nào màu trắng là \(\frac{1}{2}\).
Các bài tập cùng chuyên đề
Một túi đựng 20 viên kẹo giống hệt nhau nhưng khác loại, trong đó có 7 viên kẹo sữa, 4 viên kẹo chanh, 6 viên kẹo dừa và 3 viên kẹo bạc hà. Bạn Lan lấy ngẫu nhiên một viên kẹo từ túi. Tính xác suất để Lan lấy được
a) Viên kẹo sữa;
b) Viên kẹo chanh
Trên giá sách của thư viện có 15 cuốn sách, trong đó có một số cuốn tiểu thuyết. Người thủ thư đặt thêm 5 cuốn tiểu thuyết thư viện mới mua vào giá sách. Bạn Nam đến mượn sách, chọn ngẫu nhiên một cuốn sách trên giá. Biết rằng xác suất để chọn được cuốn tiểu thuyết là \(\frac{3}{4}\). Hỏi lúc đầu trên giá sách có bao nhiêu cuốn tiểu thuyết?
Một túi đựng 17 viên bi cùng khối lượng và kích thước, chỉ khác màu, trong đó có 8 viên bi màu đỏ, 5 viên bi màu xanh, 4 viên bi màu vàng. Lấy ngẫu nhiên một viên bi từ trong túi. Tính xác suất của biến cố E: “lấy được viên bi màu đỏ”
Tròn: Có 17 viên bi nên có 17 kết quả có thể. Có 8 viên bi màu đỏ nên có 8 kết quả thuận lợi cho biến cố E. Vậy \(P\left( E \right) = \frac{8}{{17}}\).
Vuông: Các viên bi cùng khối lượng và kích thước, chỉ khác màu, nen chỉ có 3 kết quả có thể là viên bi đỏ màu đỏ, viên bi màu trắng và viên bi màu vàng. Do đó \(P\left( E \right) = \frac{1}{3}\)
Vuông và tròn ai nói đúng? Vì sao?
Một hình tròn được chia thành 20 hình quạt như nhau, đánh số từ 1; 2;...; 20 và được gắn vào trục quat có mũi tên cố định ở tâm. Quay tấm bìa và quan sát xem mũi tên chỉ vào hình quạt nào khi tấm bìa dừng lại. Tính xác suất để mũi tên:
a) Chỉ vào hình quạt ghi số chia hết cho 4
b) Chỉ vào hình quạt ghi số không phải là số nguyên tố
Một túi đựng các viên kẹo giống hệt nhau, chỉ khác màu, trong đó có 5 viên kẹo màu đen, 3 viên kẹo màu đỏ, 7 viên kẹo màu trắng. Lấy ngẫu nhiên một viên kẹo trong túi.
Tính xác suất của các biến cố sau:
a) E: "Lấy được viên kẹo màu đen"
b) F: "Lấy được viên kẹo màu đen hoặc màu đỏ"
c) G: "Lấy được viên kẹo màu trắng"
d) H: "Không lấy được viên kẹo màu đỏ"
Trong một chiếc hộp có 15 tấm thẻ giống nhau được đánh số 10; 11;...; 24. Rút ngẫu nhiên một tấm thẻ từ trong hộp. Tính xác suất của các biến cố sau:
a) A: "Rút được tấm thẻ ghi số lẻ"
b) B: "Rút được tấm thẻ ghi số nguyên tố"
Trò chơi vòng quay may mắn.
Một bánh xe hình tròn được chia thành 12 hình quạt như nhau, trong đó có 2 hình quạt ghi 100 điểm, 2 hình quạt ghi 200 điểm, 2 hình quạt ghi 300 điểm, 2 hình quạt ghi 400 điểm, 1 hình quạt ghi 500 điểm, 2 hình quạt ghi 1000 điểm, 1 hình quạt ghi 2000 điểm. Ở mỗi lượt, người chơi quay bánh xe. Mũi tên cố định gắn trên vành bánh xe dừng ở hình quạt nào thì người chơi nhận được số điểm ghi trên hình quạt đó
Bạn Lan chơi trò chơi này. Tính xác suất của biến cố sau:
a) A: "Trong một lượt quay, Lan quay được 400 điểm"
b) B: "Trong một lượt quay, Lan được ít nhất 500 điểm"
Một túi đựng các quả bóng giống hệt nhau, chỉ khác màu, trong đó có 15 quả bóng màu xanh, 13 quả bóng màu đỏ và 17 quả bóng màu trắng. Lẫy ngẫu nhiên một quả bóng từ trong túi. Tính xác suất của các biến cố sau:
a) C: "Lấy được quả bóng màu xanh"
b) D: "Lấy được quả bóng màu đỏ"
c) E: "Không lấy được quả bóng màu trắng"
Gieo một con xúc xắc cân đối. Tính xác xuất của biến cố sau:
a) A: "Số chấm xuất hiện trên con xúc xắc khác 6"
b) B: "Số chấm xuất hiện trên con xúc xắc bé hơn 3"
c) C: "Số chấm xuất hiện trên con xúc xắc lớn hơn 2"
d) D: "Số chấm xuất hiện trên con xúc xắc là số nguyên tố"
Lớp 8A gồm 38 học sinh, trong đó có 18 bạn nữ. Có 6 bạn nữ tham gia câu lạc bộ thể thao và 8 bạn nam không tham gia câu lạc bộ thể thao. Chọn ngẫu nhiên một học sinh trong lớp
Xác suất để học sinh đó là một bạn nam có tham gia câu lạc bộ thể thao là
A. \(\frac{7}{{20}}\)
B. \(\frac{6}{{19}}\)
C. \(\frac{8}{{21}}\)
D. \(\frac{9}{{23}}\)
Lớp 8A gồm 38 học sinh, trong đó có 18 bạn nữ. Có 6 bạn nữ tham gia câu lạc bộ thể thao và 8 bạn nam không tham gia câu lạc bộ thể thao. Chọn ngẫu nhiên một học sinh trong lớp
Xác suất để học sinh đó là một bạn không tham gia câu lạc bộ thể thao là:
A. \(\frac{{11}}{{20}}\)
B. \(\frac{{12}}{{19}}\)
C. \(\frac{{13}}{{21}}\)
D. \(\frac{{10}}{{19}}\)
Một túi đựng các quả cầu giống hệt nhau, chỉ khác màu, trong đó có 26 quả màu đỏ, 62 quả màu tím, 8 quả màu vàng, 9 quả màu trắng và 12 quả màu đen. Lấy ngẫu nhiên một quả cầu trong túi
Xác suất để lấy được quả cầu màu tím là
A. \(\frac{{62}}{{117}}\)
B. \(\frac{{60}}{{117}}\)
C. \(\frac{{63}}{{118}}\)
D. \(\frac{{65}}{{118}}\)
Một túi đựng các quả cầu giống hệt nhau, chỉ khác màu, trong đó có 26 quả màu đỏ, 62 quả màu tím, 8 quả màu vàng, 9 quả màu trắng và 12 quả màu đen. Lấy ngẫu nhiên một quả cầu trong túi
Xác suất để lấy được quả cầu màu trắng là
A. \(\frac{{11}}{{117}}\)
B. \(\frac{9}{{117}}\)
C. \(\frac{{13}}{{118}}\)
D. \(\frac{{15}}{{118}}\)
Chọn ngẫu nhiên một số có hai chữ số. Tính xác suất của các biến cố sau:
a) A: "Số được chọn nhỏ hơn 20"
b) B: "Số được chọn là số chính phương
Trong một phòng học có 15 học sinh lớp 8A gồm 9 bạn nam, 6 bạn nữ và 15 học sinh lớp 8B gồm 12 bạn nam, 3 bạn nữ. Chọn ngẫu nhiên một học sinh trong phòng. Tính xác suất của các biến cố sau:
a) E: "Chọn được một học sinh nam"
b) F: "Chọn được một học sinh nam lớp 8B"
c) G: "Chọn được một học sinh nữ lớp 8A"
Một túi đựng 24 viên bi giống hệt nhau và chỉ khác màu, trong đó có 9 viên bi màu đỏ, 6 viên bi màu xanh, 4 viên bi màu vàng và 5 viên bi màu đen. Bạn An lấy ngẫu nhiên một viên bi từ trong túi
a) Có bao nhiêu kết quả có thể? Các kết quả có thể này đồng khả năng không? Tại sao
b) Tính khả năng để xảy ra mỗi kết quả có thể đó
c) Tính xác suất để An lấy được:
- Viên bi màu vàng hoặc màu đỏ
- Viên bi màu đen hoặc màu xanh
- Viên bi không có màu đen
Gieo một con xúc xắc cân đối đồng và đồng chất. Gọi \(A\) là biến cố gieo được mặt có số chấm chia hết cho 3. Tính xác suất của biến cố \(A\).
Hãy trả lời câu hỏi ở trang (88)
Một hộp có 1 quả bóng xanh và 4 quả bóng đỏ có kích thước và khối lượng như nhau. Châu lấy ra ngẫu nhiên 1 quả bóng từ hộp. Theo em, khả năng Châu lấy được bóng đỏ bằng mấy lần khả năng Châu lấy được bóng xanh.?
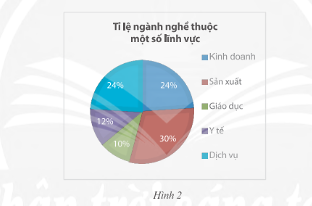
Một khu phố có 200 người lao động, mỗi người làm việc ở trong năm lĩnh vực là Kinh doanh, Sản xuất, Giáo dục, Y tế và Dịch vụ. Biểu đồ trong Hình 2 thông kê tỉ lệ người lao động thuộc mỗi lĩnh vực nghề nghiệp.
Gặp ngẫu nhiên một người lao động của khu phố.
a) Tính xác suất người đó có công việc thuộc lĩnh vực Giáo dục.
b) Tính xác suất người đó có công việc không thuộc lĩnh vực Y tế hay Dịch vụ.
Trong hộp có 5 quả bóng có kích thước và khối lượng giống nhau và được đánh số lần lượt là 5; 8; 10; 13; 16. Lấy ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất của các biến cố:
\(A\): “Số ghi trên quả bóng là số lẻ”.
\(B\): “Số ghi trên quả bóng chia hết cho 3”.
\(C\): “Số ghi trên quả bóng lớn hơn 4”.
Một hộp chứ 3 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng có kích thước và khối lượng giống nhau. Lấy ra ngẫu nhiên 1 viên bi từ hộp. Tính xác suất của các biến cố:
\(A\): “Viên bi lấy ra có màu xanh”.
\(B\): “Viên bi lấy ra không có màu đỏ”.
Trong hộp có 10 tấm thẻ cùng loại, trên mỗi tấm thẻ có ghi một số tự nhiên. Lấy ra ngẫu nhiên 1 thẻ từ hộp. Biết rằng xác suất lấy được thẻ ghi số chẵn gấp 4 lần xác suất lấy được thẻ ghi số lẻ. Hỏi trong hộp có bao nhiêu thẻ ghi số lẻ?
Số lượng học sinh tham gia Câu lạc bộ Cờ vua của một trường được biểu diễn ở biểu đồ sau:
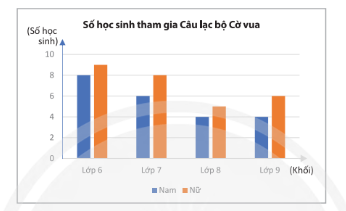
Chọn ngẫu nhiên 1 học sinh trong Câu lạc bộ Cờ vua của trường đó. Tính xác suất các biến cố:
\(A\): “Học sinh được chọn là nữ”.
\(B\): “Học sinh được chọn học lớp 8”.
\(C\): “Học sinh được chọn là nam và không học lớp 7”.
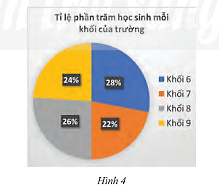
Một trường trung học có sở có 600 học sinh. Tỉ lệ phần trăm học sinh mỗi khối được cho bởi biểu đồ trong Hình 4. Chọn ngẫu nhiên một học sinh trong trường để dự phỏng vấn. Biết rằng mọi học sinh của trường đều có khả năng được lựa chọn như nhau.
a) Tính xác suất của biến cố “Học sinh được chọn thuộc khối 9”.
b) Tính xác suất của biến cố “Học sinh được chọn không thuộc khối 6”.
Một hộp chứa 10 tấm thẻ cùng loại được đánh số từ 4 đến 13. Hà lấy ra ngẫu nhiên 1 thẻ từ hộp. Xác suất để thẻ chọn ra ghi số nguyên tố là
A. 0,2.
B. 0,3.
C. 0,4 .
D. 0,5.
Vinh gieo 3 con xúc xắc cân đối và đồng chất. Xác suất của biến cố “Tích số chấm xuất hiện trên ba con xúc xắc bằng 28” là
A. 0.
B. \(\frac{1}{{36}}\).
C. \(\frac{1}{{18}}\).
D. \(\frac{1}{{12}}\).
Một hộp chứa 6 tấm thẻ cùng loại được đánh số lần lượt là 2; 3; 5; 8; 13; 21. Lấy ra ngẫu nhiên 1 thẻ từ hộp. Tính xác suất của các biến cố:
\(A\): “Số ghi trên thẻ là số chẵn”.
\(B\): “Số ghi trên thẻ là số nguyên tố”.
\(C\): “Số ghi trên thẻ là số chính phương”.
Tung đồng xu 1 lần.
a) Viết tập hợp A các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu.
b) Viết tập hợp gồm các kết quả có thể xảy ra đối với biến cố B: “Mặt xuất hiện của đồng xu là mặt N”. Mỗi phần tử của tập hợp đó gọi là một kết quả thuận lợi cho biến cố B.
c) Tìm tỉ số của số các kết quả thuận lợi cho biến cố B và số phần tử của tập hợp A.
Hình 38 mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8, chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.
Quay tròn một lần.
a) Viết tập hợp C gồm các kết quả có thể xảy ra đối với số ghi ở hình quạt mà mũi tên chỉ vào khi đĩa dừng lại.
b) Viết tập hợp gồm các kết quả có thể xảy ra đối với biến cố D: “Mũi tên chỉ vào hình quạt ghi số lẻ”. Mỗi phần tử của tập hợp đó gọi là một kết quả thuận lợi cho biến cố D.
c) Tìm tỉ số của các kết quả thuận lợi cho biến cố D và số phần tử của tập hợp C.
Trong trò chơi vòng quay số ở Hoạt động 2, tính xác suất của biến cố “Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 6”.
