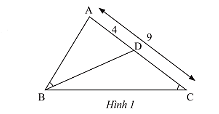
Trong Hình 1, cho biết \(\widehat {ABD} = \widehat {ACB},AC = 9cm,AD = 4cm\).
a) Chứng minh tam giác \(\Delta ABD\backsim\Delta ACB\).
b) Tính độ dài cạnh \(AB\).
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
- Nếu \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = k\)
a) Xét tam giác \(ABD\) và tam giác \(ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (giả thuyết)
\(\widehat A\) chung
Suy ra, \(\Delta ABD\backsim\Delta ACB\) (g.g)
b) Vì \(\Delta ABD\backsim\Delta ACB\)
Suy ra, \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Suy ra, \(A{B^2} = AC.AD = 9.4 = 36 \Rightarrow AB = \sqrt {36} = 6\)
Vậy \(AB = 6cm.\)
Các bài tập cùng chuyên đề
Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB=10m, \(\widehat {ABC} = {70^o}{,^{}}\widehat {BAC} = {80^o}\) và vẽ một tam giác A'B'C' trên giấy với A′B′=2cm, \(\widehat {A'B'C'} = {70^o};\widehat {B'A'C'} = {80^o}\)(H.9.20b)
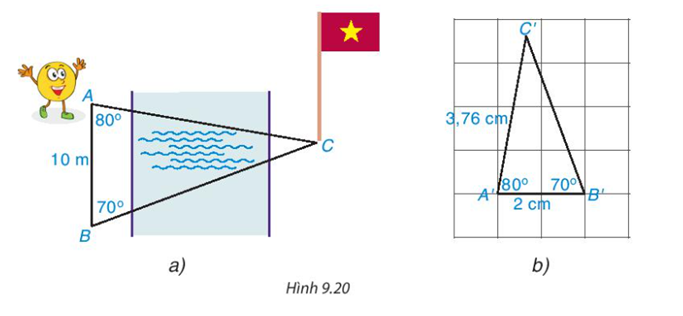
Em hãy dự đoán xem tam giác A'B'C' có đồng dạng với tam giác ABC không? nếu có thì tỉ số đồng dạng là bao nhiêu
Những cặp tam giác nào trong hình 9.22 là đồng dạng? Viết đúng kí hiệu đồng dạng
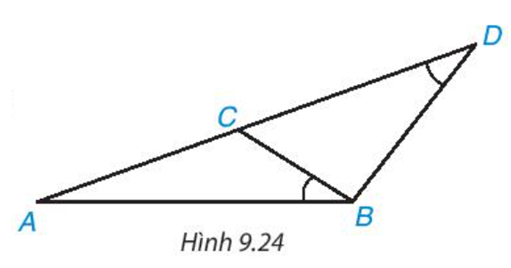
Cho các điểm A, B, C, D như Hình 9.24. Biết rằng \(\widehat {ABC} = \widehat {A{\rm{D}}B}\). Hãy chứng minh ΔABC ∽ ΔADB và \(A{B^2} = A{\rm{D}}.AC\)
1. Biết rằng ba đường phân giác của tam giác ABC đồng quy tại I, ba đường phân giác của tam giác A'B'C' đồng quy tại I'. Hãy chứng tỏ rằng nếu \( \widehat {A'I'B'} = \widehat {AIB} \) và \( \widehat {A'I'C'} = \widehat {AIC} \) thì \( \Delta A'B'C' \backsim \Delta ABC \).
2. Với hai tam giác ABC và A'B'C' trong phần Tranh luận, nếu thêm giả thiết các góc C và C' nhọn thì hai tam giác đó có đồng dạng không?
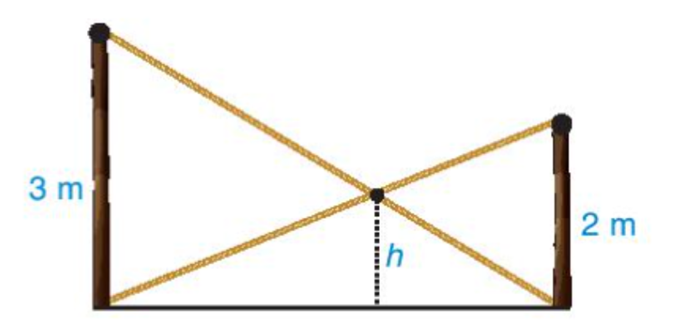
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25), hãy tính độ cao h của điểm đó so với mặt đất.
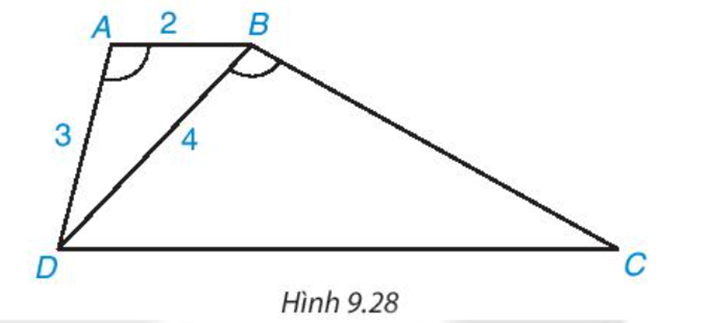
Cho hình thang ABCD (AB // CD) có \(\widehat {DAB} = \widehat {DBC}\)
a) Chứng minh rằng ΔABD ∽ ΔBDC
b) Giả sử AB=2cm,AD=3cm,BD=4cm. Tính độ dài các cạnh BC và DC
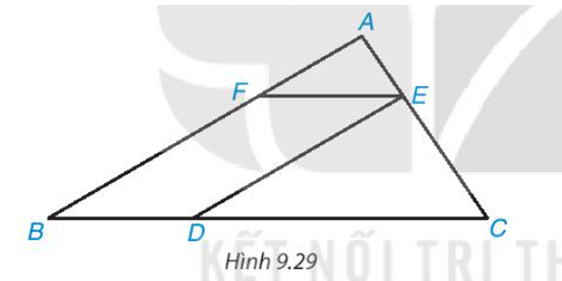
Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, DE=4cm, AB=6cm. Chứng minh rằng ΔAEF ∽ ΔECD và tính tỉ số đồng dạng
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat {BAC} = \widehat {C{\rm{D}}B}\). Chứng minh rằng ΔAED ∽ ΔBEC.
Cho hình thang ABCD (AB // CD) và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM=MD, 2BN=NC. Biết AB=5cm,CD=6cm. Hãy tính độ dài đoạn thẳng MN
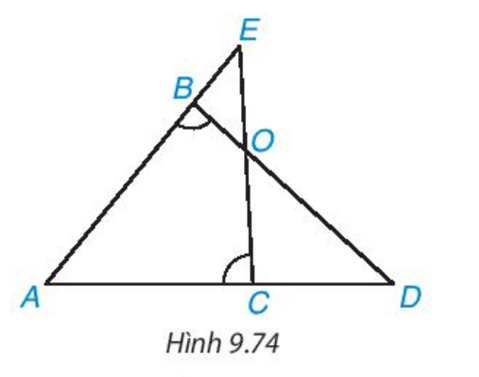
Cho hình 9.74, biết rằng \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\). Chứng minh rằng ΔABD ∽ ΔACE và ΔBOE ∽ ΔCOD
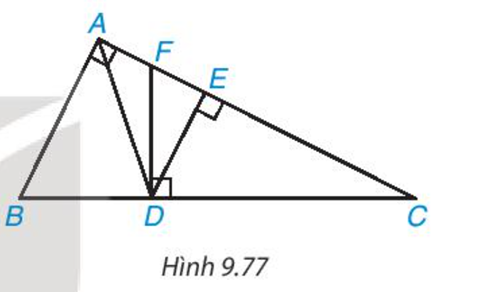
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:
a) \(\frac{{B{\rm{D}}}}{{BC}} = \frac{{AB}}{{AB + AC}}\), từ đó suy ra \(A{\rm{E}} = \frac{{AB.AC}}{{AB + AC}}\)
b) ΔDFC ∽ ΔABC
c) DF=DB
Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I. Chứng minh rằng
a) ΔBIC \(\backsim\) ΔEIF
b) \(F{B^2} = FI.FC\)
c) Cho biết AB = 6cm, BC = 3 cm. Tính EF
Cho tam giác ABC không phải là tam giác vuông, có các đường cao BE, CF cắt nhau tại điểm H
a) Giả sử ABC là tam giác nhọn. Chứng minh rằng ΔABE \(\backsim\) ΔACF , từ đó suy ra ΔAEF \(\backsim\) ΔABC
b) Cho biết AB = 10 cm, BC = 15 cm và BE = 8 cm. Tính EF
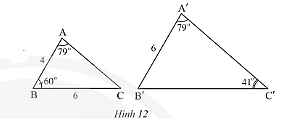
Quan sát Hình 12.
a) Chứng minh \(\Delta ABC\backsim\Delta A'B'C'\).
b) Tính độ dài cạnh \(B'C'\).
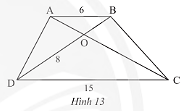
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có \(AB = 6m,CD = 15m,OD = 8m\) (Hình 13). Tính độ dài đoạn thẳng \(OB\).
Qua các trường hợp đồng dạng của hai tam giác, hãy trả lời câu hỏi ở đầu bài (trang 67).
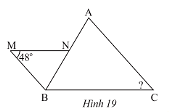
Trong Hình 19, cho biết \(MN//BC,MB//AC\)
a) Chứng minh rằng \(\Delta BNM\backsim\Delta ABC\)
b) Tính \(\widehat C\)
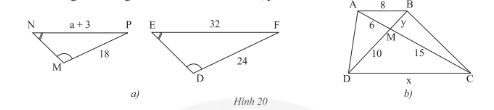
a) Trong Hình 20a, cho biết \(\widehat N = \widehat E,\widehat M = \widehat D,MP = 18m,DF = 24m,\)\(EF = 32m,\)\(NP = a + 3\left( m \right)\). Tìm \(a\).
b) Cho \(ABCD\) là hình thang \(\left( {AB//CD} \right)\) (Hình 20b).
Chứng minh rằng \(\Delta AMB\backsim\Delta CMD\). Tìm \(x,y\).
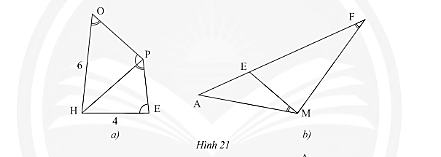
a) Trong Hình 21a, cho biết \(\widehat {HOP} = \widehat {HPE},\widehat {HPO} = \widehat {HEP},OH = 6cm\) và \(HE = 4cm\). Tính độ dài đoạn thẳng \(HP\).
b) Trong Hình 21b, cho biết \(\widehat {AME} = \widehat {AFM}\). Chứng minh rằng \(A{M^2} = AE.AF\).
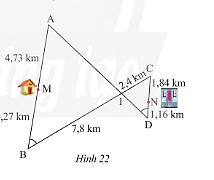
Đường đi và khoảng cách từ nhà anh Thanh (điểm \(M\)) đến công ty (điểm \(N\)) được thể hiện trong Hình 22. Hãy tìm con đường ngắn nhất để đi từ nhà anh Thanh đến công ty.
Nếu tam giác \(ABC\) và tam giác \(EFG\) có \(\widehat A = \widehat E;\widehat B = \widehat F\) thì
A. \(\Delta ABC\backsim\Delta EGF\).
B. \(\Delta ABC\backsim\Delta EFG\).
C. \(\Delta ACB\backsim\Delta GFE\).
D. \(\Delta CBA\backsim\Delta FGE\).
Cho hình thang \(ABCD\left( {AB//CD} \right)\), có hai đường chéo \(AC\) và \(DB\) cắt nhau tại \(O\). Biết \(AB = 8cm,CD = 20cm\). Khi đó \(\Delta AOB\backsim\Delta COD\) với tỉ số đồng dạng là
A.\(k = \frac{2}{3}\).
B. \(k = \frac{3}{2}\).
C. \(k = \frac{2}{5}\).
D. \(k = \frac{5}{2}\).
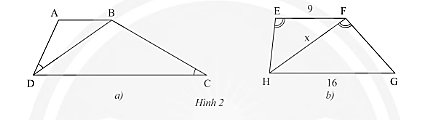
a) Cho hình thang \(ABCD\left( {AB//CD} \right)\), biết \(\widehat {ADB} = \widehat {DCB}\) (Hình 2a).
Chứng minh rằng \(B{D^2} = AB.CD\).
b) Cho hình thang \(EFGH\left( {FF//GH} \right),\widehat {HEF} = \widehat {HFG},EF = 9m,GH = 16m\) (Hình 2b).
Tính độ dài \(x\) của \(HF\).
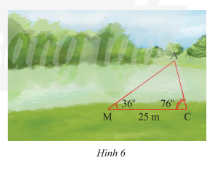
Quan sát Hình 6. Vẽ vào tờ giấy tam giác \(DEF\) với \(EF = 4cm,\widehat E = 36^\circ ,\widehat F = 76^\circ \).
a) Chứng minh \(\Delta DEF\backsim\Delta AMC\).
b) Dùng thước đo chiều dài cạnh \(DF\) của \(\Delta DEF\). Tính khoảng cách giữa hia điểm \(A\) và \(C\) ở hai bờ sông trong Hình 6.
Cho hai tam giác ABC và MNP thỏa mãn \(\widehat A = 50^\circ ,\,\,\widehat B = 60^\circ ,\,\,\widehat N = 60^\circ ,\,\,\widehat P = 70^\circ \). Chứng minh \(\Delta ABC \backsim \Delta MNP\).
Cho hai tam giác ABC và A’B’C’ có \(\widehat {A'} = \widehat A = 90^\circ ,\,\,\widehat {B'} = \widehat B\) (Hình 84). Chứng minh \(\Delta A'B'C' \backsim \Delta ABC\).
Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh \(HA.HD = HB.HE\).
Cho Hình 86.
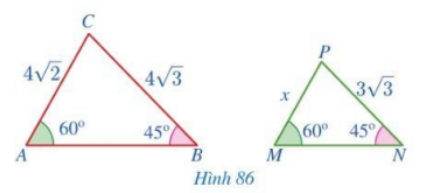
a) Chứng minh \(\Delta MNP \backsim \Delta ABC\)
b) Tìm \(x\).
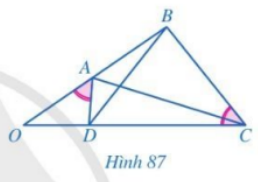
Cho Hình 87 với \(\widehat {OAD} = \widehat {OCB}\). Chứng minh:
a) \(\Delta OAD \backsim \Delta OCB\)
b) \(\frac{{OA}}{{OD}} = \frac{{OC}}{{OB}}\)
c) \(\Delta OAC \backsim \Delta ODB\)
Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:
a) \(\Delta ABC \backsim \Delta HBA\) và \(A{B^2} = BC.BH\)
b) \(\Delta ABC \backsim \Delta HAC\) và \(A{C^2} = BC.CH\)
c) \(\Delta ABH \backsim \Delta CAH\) và \(A{H^2} = BH.CH\)
d) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)
