a) Hãy đo chiều dài và chiều rộng cái bàn học của em và tính tỉ số giữa hai kích thước này.
b) Quãng đường từ Thành phố Hồ Chí Minh đi Mỹ Tho là 70 km, quãng đường từ Thành phố Hồ Chí Minh đi Cà Mau là 350 km. Tính tỉ số giữa hai quãng đường này.
c) Cho biết \(\frac{{AB}}{{CD}} = \frac{3}{5}\) và \(AB = 6cm\). Hãy tính \(CD\).
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
a) Chiều dài của cái bàn học của em là \(120cm\); chiều rộng của cái bàn học của em là \(70cm\). Tỉ số giữa chiều dài và chiều rộng của cái bàn là: \(CD:CR = \frac{{CD}}{{CR}} = \frac{{120}}{{70}} = \frac{{12}}{7}\).
b) Tỉ số giữa hai quãng đường từ Thành phố Hồ Chí Minh đi Mỹ Tho và từ Thành phố Hồ Chí Minh đi Cà Mau là: \(70:350 = \frac{{70}}{{350}} = \frac{1}{5}\).
c) Ta có: \(\frac{{AB}}{{CD}} = \frac{3}{5}\) mà \(AB = 6cm \Rightarrow \frac{6}{{CD}} = \frac{3}{5} \Rightarrow CD = \frac{{5.6}}{3} = 10cm\)
Vậy \(CD = 10cm\).
Các bài tập cùng chuyên đề
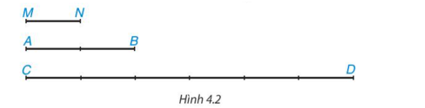
Cho Hình 4.2, em hãy thực hiện các hoạt động sau:
Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\)
Cho Hình 4.2, em hãy thực hiện các hoạt động sau:
Dùng thước thẳng, đo độ dài hai đoạn thẳng AB và CD (đơn vị: cm) rồi dùng kết quả vừa đo để tính tỉ số \(\dfrac{{AB}}{{C{\rm{D}}}}\)
So sánh hai tỉ số tìm được trong hai hoạt động trên
Tính tỉ số của các đoạn thẳng có độ dài như sau:
a) MN = 3 cm và PQ = 9 cm.
b) EF = 25 cm và HK = 10 dm.
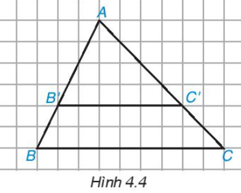
Cho tam giác ABC và một điểm B’ nằm trên cạnh AB. Qua điểm B’, ta vẽ một đường thẳng song song với BC, cắt A tại C’ (H.4.4
Dựa vào hình vẽ, hãy tính và so sánh các tỉ số sau và viết các tỉ lệ thức:
a) \(\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\)
b) \(\dfrac{{AB'}}{{B'B}}\) và \(\dfrac{{AC'}}{{C'C}}\)
c) \(\dfrac{{B'B}}{{AB}}\) và \(\dfrac{{C'C}}{{AC}}\)
Viết tỉ số của các cặp đoạn thẳng có độ dài như sau:
a) \(HK = 3cm\) và \(MN = 9cm\);
b) \(AB = 36cm\) và \(PQ = 12dm\);
c) \(EF = 1,5m\) và \(GH = 30cm\).
Cho hình bình hành ABCD có M, N lần lượt là trung điểm AB và CD. Gọi P, Q theo thứ tự là giao điểm của AN và CM với đường chéo BD. Chứng minh rằng: \(DP = PQ = QB\)
Cho AB = 10 cm; MN = 3 dm. Tỉ số nào đúng?
A. \(\frac{{AB}}{{MN}} = \frac{{10}}{3}.\)
B. \(\frac{{AB}}{{MN}} = \frac{3}{{10}}.\)
C. \(\frac{{AB}}{{MN}} = \frac{1}{3}.\)
D. \(\frac{{AB}}{{MN}} = 3.\)
a) Cho hai số 5 và 8. Hãy tính tỉ số giữa hai số đã cho.
b) Hãy đo và tính tỉ số giữa hai độ dài (theo mm) của hai đoạn thẳng \(AB\) và \(CD\) trong Hình 1.
Hãy tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) trong các trường hợp sau:
a) \(AB = 6cm;CD = 8cm\);
b) \(AB = 1,2m;CD = 42cm\).
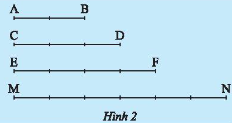
So sánh tỉ số của hai đoạn thẳng \(AB\) và \(CD\) với tỉ số của hai đoạn thẳng \(EF\) và \(MN\) trong Hình 2.
Trong Hình 3, chứng minh rằng:
a) \(AB\) và \(BC\) tỉ lệ với \(A'B'\) và \(B'C'\);
b) \(AC\) và \(A'C'\) tỉ lệ với \(AB\) và \(A'B'\).
Hãy tìm các đoạn thẳng tỉ lệ trong hình vẽ sơ đồ một góc công viên ở Hình 4.
Trên một tờ giấy kẻ caro có các đường kẻ ngang song song và cách đều nhau.
a) Vẽ một đường thẳng \(d\) cắt các đường kẻ ngang của tờ giấy như trong Hình 5a. Hãy so sánh độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\).
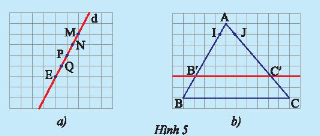
b) Vẽ một tam giác \(ABC\) rồi vẽ một đường thẳng song song với cạnh \(BC\) và cắt hai cạnh \(AB,AC\) lần lượt tại \(B'\) và \(C'\). Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo tính tỉ số \(AB'\) và \(BB'\); trên cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo tính tỉ số \(AC'\) và \(C'C\) (Hình 5b).
So sánh các tỉ số \(\frac{{AB'}}{{AB}}\) và \(\frac{{AC'}}{{AC}}\);\(\frac{{AB'}}{{B'B}}\) và \(\frac{{AC'}}{{C'C}}\);\(\frac{{B'B}}{{AB}}\) và \(\frac{{C'C}}{{AC}}\).
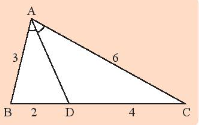
Đường phân giác \(AD\) của tam giác \(ABC\) chia cạnh đối diện \(BC\) thành hai đoạn thẳng tỉ lệ với hai đoạn thẳng nào trong hình?
Cho hai đoạn thẳng \(AB = 12cm\) và \(CD = 18cm\). Tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) là
A. \(\frac{4}{3}\).
B. \(\frac{3}{4}\).
C. \(\frac{2}{3}\).
D. \(\frac{3}{2}\).
Cho hai đoạn thẳng AB = 2cm, CD = 3cm và hai đoạn thẳng MN = 4cm, PQ = 6cm. So sánh hai tỉ số \(\frac{{AB}}{{CD}},\,\,\frac{{MN}}{{PQ}}\).
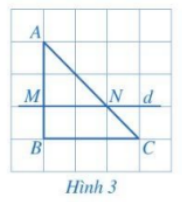
Quan sát Hình 3 và cho biết:
a) Đường thẳng \(d\) có song song với BC hay không?
b) Bằng cách đếm số ô vuông, dự đoán xem các tỉ số \(\frac{{AM}}{{MB}},\frac{{AN}}{{NC}}\) có bằng nhau hay không?
Đối với mỗi chiếc lá phong trong hình \(6.2,\) hãy đo chiều rộng \(AB;A'B'\) và chiều dài \(CD;C'D'\) (với đơn vị là centimét).
1. Tính tỉ số độ dài \(AB\) và \(CD.\)
2. Tính tỉ số độ dài \(A'B'\) và \(C'D'.\)
Em có nhận xét gì về hai tỉ số trên?
Trong hình 6.4, độ dài các đoạn thẳng được viết với cùng đơn vị đo. Tính các tỉ số \(\frac{{AB}}{{BC}},\frac{{BC}}{{AC}}\) và cho biết hai đoạn thẳng \(AB\) và \(BC\) có tỉ lệ với đoạn thẳng \(BC\) và \(AC\) không.
Giấy vở học sinh có các đường kẻ song song và cách đều nhau. Khi vẽ một đường thẳng bất kì cắt các đường kẻ, ta được các đoạn thẳng liên tiếp bằng nhau (Hình 6.5a). Xét \(\Delta ABC\) trong hình 6.5b.
1. Chọn \(BD\) làm đơn vị đo độ dài, em hãy tính độ dài \(AD,AB\) và các tỉ số \(\frac{{DA}}{{DB}},\frac{{AD}}{{AB}},\frac{{BD}}{{BA}}.\)
2. Chọn \(CE\) làm đơn vị đo độ dài, em hãy tính độ dài \(AE,AC\) và các tỉ số \(\frac{{EA}}{{EC}},\frac{{AE}}{{AC}},\frac{{CE}}{{CA}}.\)
3. So sánh các cặp tỉ số\(\frac{{DA}}{{DB}}\) và \(\frac{{EA}}{{EC}},\frac{{AD}}{{AB}}\) và \(\frac{{AE}}{{AC}},\frac{{BD}}{{BA}}\) và \(\frac{{CE}}{{CA}}.\) Em có nhận xét gì về các cặp đoạn thẳng được cho?
Tính tỉ số các cặp đoạn thẳng sau và cho biết các cặp đoạn thẳng nào tỉ lệ với nhau:
a) \(AB = 5dm\) và \(CD = 40cm;\)
b) \({\rm{EF}} = 10cm\) và \(GH = 8cm;\)
c) \(KL = 15mm\) và \(MN = 120mm.\)
Cho ba điểm \(A,B,C\) thẳng hàng, trong đó \(B\) nằm giữa \(A,C\) và \(\frac{{AB}}{{BC}} = \frac{3}{5}.\) Tính tỉ số của:
a) Hai đoạn thẳng \(AC\) và \(BC;\)
b) Hai đoạn thẳng \(AB\) và \(AC.\)
