Lam phụ giúp mẹ bánh nước chanh, em nhận thấy số ly nước chanh \(y\) bán được trong ngày và nhiệt độ trung bình \(x\left( {^\circ C} \right)\) của ngày hôm đó có mối tương quan. Lan ghi lại các giá trị tương ứng của hai đại lượng \(x\) và \(y\) trong bảng sau:
Cho biết đường thẳng \(d:y = mx\) đi qua các điểm \(A;B;C;D;E;F\) ở câu a. Tìm hệ số góc của \(d\).
Thay tọa độ của điểm thuộc đường thẳng vào phương trình đường thẳng để tìm m.
Vì đường thẳng \(d:y = mx\) đi qua các điểm \(A;B;C;D;E;F\) nên ta chọn \(A\left( {20;10} \right)\) thay vào đường thẳng ta được:
\(10 = 20.m \Leftrightarrow m = 10:20 \Leftrightarrow m = \dfrac{1}{2}\)
Do đó đường thẳng cần tìm là: \(y = \dfrac{1}{2}x\).
Hệ số góc của đường thẳng là \(a = \dfrac{1}{2}\).
Các bài tập cùng chuyên đề
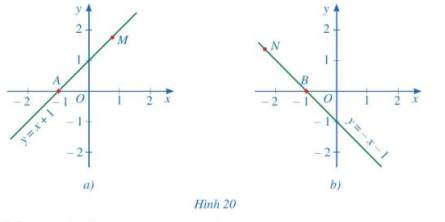
Quan sát đường thẳng y = x +1 và y = -x – 1 (hình 20)
a) Tung độ các điểm M, N là số dương hay số âm?
b) Tìm góc tạo bởi hai tia Ax và AM ở hình 20a?
c) Tìm góc tạo bởi tia Bx và BN ở hình 20b?
Hình 22a, biểu diễn đồ thị của các hàm số bậc nhất: y = 0,5x + 2; y = 2x + 2. Hình 22b biểu diễn đồ thị của các hàm số bậc nhất: y = -2x + 2; y = -0,5x + 2
a) Quan sát hình 22a, so sánh các góc \(\alpha ,\beta \) và so sánh các giá trị tương ứng của hệ số của x trong các hàm số bậc nhất rồi rút ra nhận xét.
b) Quan sát hình 22b, so sánh các góc \(\alpha ',\beta '\) và so sánh các giá trị tương ứng của hệ số của x trong các hàm số bậc nhất rồi rút ra nhận xét.
Tìm hệ số góc của đường thẳng y = -5x + 11
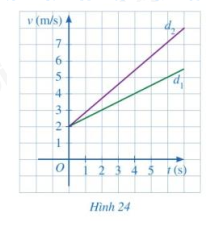
Một phần đường thẳng \({d_1},{d_2}\) ở Hình 24 lần lượt biểu thị tốc độ (đơn vị: m/s) của vật thứ nhất, vật thứ hai theo thời gian t (s)
a) Nêu nhận xét về tung độ giao điểm của hai đường thẳng \({d_1},{d_2}\). Từ đó, nêu nhận xét về tốc độ của hai chuyển động.
b) Trong hai đường thẳng \({d_1},{d_2}\), đường thẳng nào có hệ số góc lớn hơn?
c) Từ giây thứ nhất trở đi, vật nào có tốc độ lớn hơn? Vì sao?
Cho các đường thẳng \({d_1}:y = 11x + 1;{d_2}:y = \sqrt 3 x - 7;{d_3}:y = 2x - \sqrt 2 \). Gọi \({\alpha _1},{\alpha _2},{\alpha _3}\) lần lượt là các góc tạo bởi đường thẳng \({d_1},{d_2},{d_3}\) và trục \(Ox\). Sắp xếp các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) theo thứ tự số đo tăng dần.
Trên cùng một mặt phẳng tọa độ Oxy, vẽ hai đường thẳng sau:
(d): y=2x+1 và (d'): y=−2x+1
a) So sánh góc tạo bởi đường thẳng (d) và trục Ox với 90°
b) So sánh góc tạo bởi đường thẳng (d') và trục Ox với 90°
Từ kết quả của hoạt động 1, em có nhận xét gì về quan hệ giữa hệ số a của đường thẳng y=ax+b (a≠0) với góc tạo bởi đường thẳng này và trục Ox
Xác định hệ số góc của mỗi đường thẳng sau:
\(y = 3{\rm{x}} - 1\); \(y = 2 - x\); \(y = \frac{1}{2}\left( {x - 1} \right)\)
Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là 3 và cắt trục tung tại điểm có tung độ bằng -1
Đường thẳng \(y = \frac{{2{\rm{x}} + 1}}{2}\) có hệ số góc bằng bao nhiêu?
Tròn: Đường thẳng này có hệ số góc a = 2
Vuông: Không đúng, đường thẳng này có hệ số góc a = 1
Theo em, bạn nào trả lời đúng, bạn nào trả lời sai? Vì sao?
Tìm hàm số bậc nhất có đồ thị là đường thẳng đi qua điểm (1;-2) và có hệ số góc là 3.
Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là -2 và cắt trục hoành tại điểm có hoành độ bằng 3.
Đường thẳng có hệ số góc bằng 2 và đi qua điểm (-1;2) là:
A. y=2x+2
B.y=2x−1
C. y=−x+2
D. y=2x+4
Tìm hệ số góc của các đường thẳng sau đây:
a) \(y = - 5x - 5\);
b) \(y = \sqrt 3 x + 3\);
c) \(y = \sqrt {11} x + \sqrt 7 \)
Trong các đường thẳng sau, đường thẳng nào tạo với \(Ox\) một góc nhọn, đường thẳng nào tạo với \(Ox\) một góc tù?
a) \(y = 3x + 6\);
b) \(y = - 4x + 1\);
c) \(y = - 3x - 6\)
a) Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) cắt \(Ox\) tại điểm \(A\) và \(T\) là một điểm trên đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có tung độ dương (Hình 1).
Ta gọi \(\alpha = \widehat {xAT}\) là góc tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \(Ox\).
Hãy nêu nhận xét của em về số đo của góc \(\alpha \) và hệ số \(a\) trong hai trường hợp dưới đây.
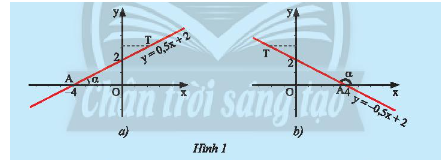
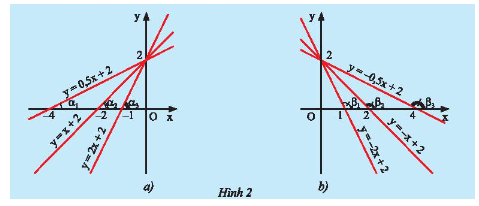
b) Hãy so sánh các hệ số \(a\) của các đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) trong mỗi hình ở Hình 2 và so sánh các góc \(\alpha \) hoặc các góc \(\beta \) tạo bởi các đường thẳng đó với trục \(Ox\).
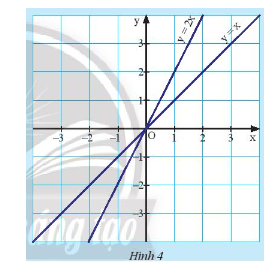
Quan sát Hình 4.
a) Tìm giao điểm của hai đường thẳng \(d:y = 2x\) và \(d':y = x\).
b) Nêu nhận xét về hai đường thẳng có hệ số góc khác nhau.
c) Cho đường thẳng \(d':y = ax + b\) và cho biết \(d''\) cắt \(d\). Hệ số góc \(a\) của đường thẳng \(d''\) có thể nhận giá trị nào?
Cho hàm số bậc nhất \(y = ax - 4\)
a) Tìm hệ số góc \(a\) biết rằng đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\).
b) Vẽ đồ thị của hàm số.
a) Vẽ đồ thị của hàm số \(y = x\) và \(y = x + 2\) trên cùng một mặt phẳng tọa độ.
b) Dùng thước đo góc để tìm góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\).
Một xe khách khởi hành từ bến xe phía Nam bưu điện thành phố Huế để đi vào thành phố Quy Nhơn với tốc độ 50 \(km/h\).
Tìm hệ số góc của đường thẳng là đồ thị của hàm số \(y\) ở câu a.
Cho biết đồ thị của hàm số \(y = ax\) đi qua điểm \(P\left( {1; - \dfrac{4}{5}} \right)\). Xác định hệ số \(a\).
Cho hai hàm số \(y = x + 3\), \(y = - x + 3\) có đồ thị lần lượt là các đường thẳng \({d_1}\) và \({d_2}\). Dùng thước đo góc để tìm góc tạo bởi \({d_1}\) và \({d_2}\) lần lượt với trục \(Ox\).
Hình 5.26 biểu diễn đồ thị của các hàm số bậc nhất \(y = 2x + 3,y = 2x\) và \(y = 2x - 4\). So sánh hệ số a của các hàm số trên. So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) .
a) Hình 5.28a biểu diễn đồ thị của các hàm số bậc nhất với hệ số a > 0:
\(y = \frac{1}{2}x + 1\)
\(y = x + 1\)
\(y = 2x + 1\)
So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) và so sánh các hệ số \(a\) tương ứng của các hàm số trên rồi rút ra nhận xét.
b) Hình 5.28b biểu diễn đồ thị của các hàm số bậc nhất với hệ số a < 0:
\(y = - 2x + 1\)
\(y = - x + 1\)
\(y = - \frac{1}{2}x + 1\)
So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) và so sánh các hệ số \(a\) tương ứng của các hàm số trên rồi rút ra nhận xét.
Cho hàm số bậc nhất \(y = ax\) có đồ thị là đường thẳng d như Hình 5.29. Tìm hệ số góc a.
Trong Hình 5.30, các đường thẳng \(d\) và \(d'\) lần lượt chứa đồ thị quãng đường – thời gian của hai ô tô A và B chuyển động đều.
a) Tìm các số thích hợp cho ô trống trong Bảng 5.16.
b) Xác định hệ số góc của mỗi đường thẳng.
c) Tính tốc độ của mỗi xe. Em có nhận xét gì về tốc độ của mỗi xe và hệ số góc của đồ thị quãng đường – thời gian tương ứng?
Xác định hệ số góc của các đường thẳng sau:
a) \(y = \sqrt 3 x - 1\)
b) \(y = \frac{{5 - 2x}}{3}\)
c) \(y = 2,5\left( {x - 2} \right) - 0,5x\)
Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và điểm \(A\left( { - 1;3} \right)\).
Theo định luật Dolbear, số tiếng kêu y trong một phút của một con dế và nhiệt độ môi trường x (tính theo độ F, thang đo Fahrenheit) liên hệ với nhau theo hàm số \(y = ax - 160\).
a) Xác định số a trong công thức của định luật Dolbear, biết rằng khi nhiệt độ môi trường tăng lên \(1^\circ F\) thì con dế kêu thêm 4 tiếng trong 1 phút.
b) Khi nhiệt độ môi trường là \(70^\circ F\), theo định luật Dolbear, số tiếng kêu trong một phút của con dế là bao nhiêu?
Góc tạo bởi đường thẳng \(y=-2x+1\) với trục \(Ox\) là:
