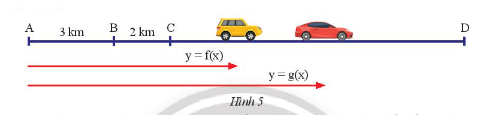
Hai ô tô khởi cùng lúc và cùng vận tốc 50 \(km/h\), một ô tô bắt đầu từ \(B\), một ô tô bắt đầu từ \(C\) và cùng đi về phía \(D\).
a) Viết công thức của hai hàm số biểu thị khoảng cách từ \(A\) đến mỗi xe sau \(x\) giờ.
b) Chứng tỏ đồ thị của hai hàm số trên là hai đường thẳng song song.
- Quãng đường vật đi được trong khoảng thời gian \(t\left( h \right)\) với vận tốc \(v\left( {km/h} \right)\) là:
\(s = v.t\)
- Khoảng cách của xe sau \(t\left( h \right)\) với một điểm là:
\(y = {y_0} + v.t\)
Với \({y_0}\) là khoảng cách của xe với điểm ở thời điểm ban đầu, \(v\) là vận tốc của xe, t là thời gian xe đã đi.
- Hai hàm số có đồ thị là hai đường thẳng song song nếu chúng phân biệt và có hệ số góc bằng nhau.
a)
- Quãng đường xe ô tô khởi hành từ \(B\) đi được sau khoảng thời gian \(x\left( h \right)\) với vận tốc 50 km/h là: \(s = v.t = 50.x\)
Khi đó, công thức biểu thị khoảng cách từ điểm \(A\) đến xe là:
\(y = {y_0} + v.t = 3 + 50.x\).
- Quãng đường xe ô tô khởi hành từ \(C\) đi được sau khoảng thời gian \(x\left( h \right)\) với vận tốc 50 km/h là: \(s = v.t = 50.x\)
Khi đó, công thức biểu thị khoảng cách từ điểm \(A\) đến xe là:
\(y = {y_0} + v.t = 5 + 50.x\).
b) Đồ thị của hai hàm số trên là hai đường thẳng phân biệt vì cắt \(Oy\) tại hai điểm phân biệt.
Hai đường thẳng đó song song với nhau vì hệ số góc của hai đường thẳng này bằng nhau (đều có \(a = 50\)).
Các bài tập cùng chuyên đề
Xác định đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {2;0} \right)\) và song song với đường thẳng \(y = 2x - 5\). Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Cho đồ thị của hàm số \(y = ax + b\) đi qua điểm \(M\left( {1;4} \right)\) và song song với đường thẳng \(y = 2x + 1\). Tích \(ab\) bằng:
A.6
B.4
C.3
D.2
Xác định đường thẳng \(d:y = ax + b\left( {a \ne 0} \right)\) trong mỗi trường hợp sau:
a) Đường thẳng \(d\) song song với đường thẳng \(d':y = - 3x - \frac{2}{3}\) và đi qua điểm \(A\left( { - 2; - 4} \right)\).
b) Đường thẳng \(d\) đi qua điểm \(B\) và có hệ số góc bằng -3. Biết \(B\) là giao điểm của đường thẳng \(y = 2x - 2\) với trục hoành.
Trên cùng một mặt phẳng tọa độ Oxy, vẽ hai đường thẳng y=2x và y=2x+1. Có nhận xét gì về vị trí tương đối của hai đường thẳng này
Liệu hai đường thẳng phân biệt có cùng hệ số góc, có thể có
a) Cùng giao điểm với trục Ox không?
b) Cùng giao điểm với trục Oy không?
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng y=−3x+1 và đi qua điểm (2;6)
Giá trị m để đường thẳng y=(m+1)x+2 song song với đường thẳng y=−2x là
A. m=−3
B.m=−2
C. m=2
D. m=1
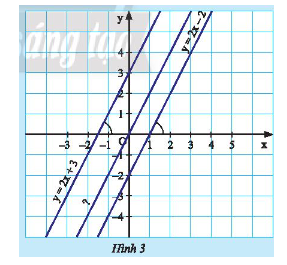
Quan sát Hình 3.
a) So sánh hệ số góc của hai đường thẳng:
\(d:y = 2x + 3\) và \(d':y = 2x - 2\).
Nêu nhận xét về vị trí giữa hai đường thẳng này.
b) Tìm đường thẳng \(d''\) đi qua gốc tọa độ \(O\) và song song với đường thẳng \(d\).
Tìm hệ số góc \(a\) để hai đường thẳng \(y = ax + 2\) và \(y = 9x - 9\) song song với nhau.
Cho đường thẳng \(d:y = x + 2023\). Xác định hai hàm số biết đồ thị của chúng là hai đường thẳng song song với \(d\).
Đường thẳng song song với đường thẳng \(y = 2x\) và cắt trục tung tại điểm có tung độ bằng 1 là:
A. \(y = 2x - 1\).
B. \(y = - 2x - 1\).
C. \(y = 2x + 1\).
D. \(y = 6 - 2\left( {1 - x} \right)\).
Tìm hàm số có đồ thị là đường thẳng song song với đồ thị hàm số \(y = - 2x + 10\).
Tìm \(m\) để các hàm số bậc nhất \(y = 2mx - 2\) và hàm số \(y = 6x + 3\) có đồ thị là những đường thẳng song song với nhau.
a) Vẽ đồ thị hai hàm số \(y = 3x - 2\) và \(y = 3x + 1\) trên cùng một mặt phẳng tọa độ.
b) Giải thích vì sao hai đường thẳng \(y = 3x - 2\) và \(y = 3x + 1\) song song với nhau.
Cho hàm số \(y = ax + 2\). Xác định hệ số a, biết đồ thị của hàm số đã cho song song với đường thẳng \(y = - 3x\).
Cho hàm số \(y = ax - 3\). Xác định hệ số a, biết rằng đồ thị của hàm số đã cho song song với đường thẳng \(y = 1 - x\).
Cho hai đường thẳng \(d:y = ax + b\,\,\left( {a \ne 0} \right)\) và \(d':y = a'x + b'\,\,\left( {a' \ne 0} \right)\). Với điều kiện nào sau đây thì hai đường thẳng \(d\) và \(d'\) song song?
Hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = -x + 2\) và cắt trục tung tại điểm có tung độ bằng 1 là
Nếu hai đường thẳng \({d_1}:y = - 3x + 4\) và \({d_2}:y = \left( {m + 2} \right)x + m\) song song với nhau thì m bằng:
A. \( - 2\)
B. 3
C. \( - 5\)
D. \( - 3\)
Đường thẳng song song với đường thẳng \(y = 5x\) và cắt trục tung tại điểm có tung độ bằng 1 là:
A. \(y = 5x - 1\)
B. \(y = - 5x - 1\)
C. \(y = 5x + 1\)
D. \(y = 4 - 5\left( {1 - x} \right)\)
Cho hai đường thẳng \(y = \frac{1}{4}x + 4\) và \(y = \frac{1}{4}x - 4\). Hai đường thẳng đã cho:
A. Cắt nhau tại điểm có hoành độ là 4.
B. Song song với nhau.
C. Cắt nhau tại điểm có tung độ là 4.
Xác định hàm số \(y = ax + b\) biết đồ thị hàm số đã cho song song với đường thẳng \(y = - 2x + 3\) và đi qua \(A\left( {1; - 3} \right)\).
Cho hai đồ thị hàm số bậc nhất là: \(y = \left( {m - 1} \right)x + 6\) và \(y = 5x + 2m - 6\).
Gía trị của \(m\) để hai đường thẳng này song song với nhau là
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = - 2x + 1\) và đi qua điểm \(\left( { - 1;4} \right)\)
Giá trị m để đường thẳng \(y = \left( {m - 1} \right)x + 3\left( {m \ne 1} \right)\) song song với đường thẳng \(y = x\) là
A. \(m = 2\)
B. \(m = 1\)
C. \(m = 0\)
D. Không có giá trị của m
Hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = - x + 2\) và cắt trục tung tại điểm có tung độ bằng 1 là:
A. \(y = x + 1\)
B. \(y = - x + 1\)
C. \(y = 1\)
D. Không có hàm số nào
Hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = - 2x\) và đi qua điểm \(A\left( {1; - 1} \right)\) là
A. \(y = 2x + 1\)
B. \(y = - 2x + 1\)
C. \(y = 1\)
D. Không có hàm số nào
