\(y = x\); \(y = x + 2\); \(y = - x\); \(y = - x + 2\).
Bốn đồ thị nói trên cắt nhau tại các điểm \(O\left( {0;0} \right),A,B,C\). Tứ giác có bốn đỉnh \(O;A;B;C\) là hình gì? Giải thích.
Tính độ dài các cạnh và góc của tứ giác.
Chú ý: Hình thoi có 1 góc vuông là hình vuông.
Vì đường thẳng \(y = x\);\(y = x + 2\) song song với nhau và \(y = - x\);\(y = - x + 2\) song song với nhau nên tứ giác \(OABC\) là hình bình hành.
Lại có \(OC;OA\) là đường chéo của hình vuông có độ dài cạnh là 1 nên \(OC = OA\). Do đó, tứ giác \(OABC\) là hình thoi.
Lại có \(OC;OA\) là đường chéo của hình vuông nên cũng là đường phân giác. Do đó, \(\widehat {COB} = \widehat {AOB} = 45^\circ \Rightarrow \widehat {COA} = \widehat {COB} + \widehat {AOB} = 45^\circ + 45^\circ = 90^\circ \)
Hình thoi \(OABC\) có góc \(\widehat {COA} = 90^\circ \) nên tứ giác \(OABC\) là hình vuông.
Các bài tập cùng chuyên đề
Xét hàm số: y = x – 2
a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:
|
x |
0 |
2 |
3 |
|
y |
? |
? |
? |
b) Vẽ các điểm A (0; -2); B(2; 0); C(3; 1) của đồ thị hàm số y = x – 2 trong mặt phẳng tọa độ Oxy. Dùng thước thẳng để kiểm tra ba điểm A, B, C có thẳng hàng hay không?
Cho hàm số y = 4x + 3. Tìm điểm thuộc đồ thị hàm số của hàm số có hoành độ bằng 0.
Cho đường thẳng \(d:y = \left( {m - 2} \right)x + 2\) với \(m \ne 2\).
a) Tìm giá trị của \(m\) để đường thẳng \(d\) cùng với các trục \(Ox,Oy\) tạo thành tam giác có diện tích bằng 2.
b) Chứng tỏ rằng khi giá trị của \(m\) thay đổi thì tập hợp các đường thẳng \(d\) luôn đi qua một điểm cố định.
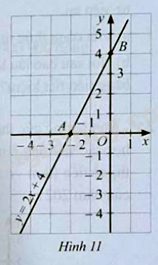
Trong mặt phẳng tọa độ \(Oxy\), cho đồ thị của hàm số \(y = 2x + 4\) (Hình 11).
a) Gọi \(A,B\) lần lượt là giao điểm của trục \(Ox,Oy\) với đồ thị hàm số \(y = 2x + 4\). Xác định tọa độ các điểm \(A,B\).
b) Gọi \(M,N\) lần lượt là trung điểm của \(OA,OB\). Xác định tọa độ các điểm \(M,N\).
c) Tính tỉ số phần trăm của diện tích tam giác \(OMN\) và diện tích tam giác \(OAB\).
Gọi A, B, C, D, E là các điểm trên đồ thị hàm số y=2x−1 có hoành độ x lần lượt là -2; -1; 0; 1; 2. Từ kết quả của HĐ4, hãy xác định tọa độ các điểm A, B, C, D, E
Trên mặt phẳng tọa độ Oxy, biểu diễn các điểm A, B, C, D, E trong HĐ5. Dùng thước thẳng để kiểm nghiệm rằng các điểm này cùng nằm trên một đường thẳng
Trong các điểm sau, điểm nào thuộc đồ thị của hàm số \(y = 2 - 4x\)?
A. \(\left( {1;1} \right)\).
B. \(\left( {2;0} \right)\).
C. \(\left( {1; - 1} \right)\).
D. \(\left( {1; - 2} \right)\).
Trong các điểm sau, điểm nào thuộc đồ thị của hàm số \(y = - 5x + 5\)?
A. \(\left( {1;1} \right)\).
B. \(\left( {2;0} \right)\).
C. \(\left( {0;4} \right)\).
D. \(\left( {2; - 5} \right)\).
Cho hai hàm số \(y = x + 3\), \(y = - x + 3\) có đồ thị lần lượt là các đường thẳng \({d_1}\) và \({d_2}\). Tính chu vi và diện tích của tam giác \(ABC\).
Cho hàm số \(y = 3x\).
a) Tìm các giá trị tương ứng của hàm số trong Bảng 5.15.
b) Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm biểu diễn các cặp giá trị \(\left( {x;y} \right)\) tương ứng trong Bảng 5.15.
c) Vẽ đường thẳng đi qua hai trong bốn điểm trên. Dùng thước thẳng kiểm tra xem đường thẳng này có đi qua hai điểm còn lại hay không.
d) Lấy thêm một cặp số \(\left( {x;y} \right)\), với x chọn tùy ý khác bốn giá trị ở trên. Đánh dấu điểm biểu diễn cặp số đó lên mặt phẳng tọa độ \(Oxy\). Dùng thước thẳng kiểm tra xem điểm vừa đánh dấu có thuộc đường thẳng đã vẽ ở câu c không.
Cho hàm số được xác định bởi công thức \(y = ax - 1\). Biết đồ thị hàm số này đi qua điểm \((1;2)\). Hoành độ của điểm thuộc đồ thị hàm số có tung độ bằng \(-4\) là
Cho đồ thị hàm số \(y = ax\) đi qua điểm \(A\left( {2; - 4} \right)\).
a) Xác định hệ số a.
b) Tìm tọa độ của điểm thuộc đồ thị có hoành độ bằng \( - 3\).
c) Tìm tọa độ của điểm thuộc đồ thị có tung độ bằng \( - 2\).
Cho hàm số \(y = 3x + 6\).
a) Vẽ đồ thị của hàm số trên mặt phẳng tọa độ Oxy.
b) Gọi A, B lần lượt là giao điểm của đồ thị hàm số trên với trục Ox, Oy. Xác định tọa độ của A, B và diện tích của tam giác AOB. (Đơn vị đo trên các trục tọa độ là cm.)
Trong các điểm sau, điểm nào thuộc đồ thị hàm số \(y = 2 - 4x\)?
A. \(\left( {1;1} \right)\)
B. \(\left( {2;0} \right)\)
C. \(\left( {1; - 1} \right)\)
D. \(\left( {1; - 2} \right)\)
Cho hàm số \(y = \left( {m - 3} \right)x\).
a) Với giá trị nào của m thì đồ thị của hàm số đã cho đi qua điểm A (1; 2)?
b) Với giá trị nào của m thì đồ thị của hàm số đã cho đi qua điểm B (1; -2)?
Tìm điểm cố định mà mỗi đường thẳng \(d':y = \left( {m - 2} \right)x + 3\) luôn đi qua với mọi giá trị của m.
Cho ba đường thẳng \(\left( {{d_1}} \right):y = - 2x + 1;\left( {{d_2}} \right):y = x + 4\) và \(\left( {{d_3}} \right):y = 2mx - 3\left( {m \ne 0} \right)\)
a) Tìm giao điểm của hai đường thẳng \(\left( {d{ _1}} \right)\) và \(\left( {{d_2}} \right)\).
b) Xác định giá trị của m để ba đường thẳng đã cho đồng quy.
Điểm (-2; 3) thuộc đồ thị hàm số nào sau đây?
A. y = -6x.
B. y = 6x.
C. y = \( - \frac{3}{2}\)x.
D. y = \( - \frac{2}{3}\)x.
Cho hàm số y = -2x + 4. Chứng tỏ rằng:
a) Điểm A(-1; 1) không thuộc đồ thị của hàm số đã cho;
b) Điểm B(3; -2) thuộc đồ thị hàm số đã cho.
Giao điểm của đồ thị hàm số bậc nhất y = -2x + 4 với trục Ox là
A. (2; 0).
B. ( 4; 0).
C. (0; 4).
D. (0; 2).
Giao điểm của đồ thị hàm số bậc nhất y = 3x - 6 với trục Oy là
A. (2; 0).
B. ( 0; -6).
C. (-6; 0).
D. (0; 2).
