Đề bài
Tìm giá trị lớn nhất, nhỏ nhất (nếu có) của hàm số: \(y = 3{x^2} - 6x + 7\) trên đoạn [-2;5].
Lời giải của GV Loigiaihay.com
Hàm số \(y = 3{x^2} - 6x + 7\) có \(a = 3 > 0,b = - 6 \Rightarrow - \frac{b}{{2a}} = 1;\;y(1) = 4\).
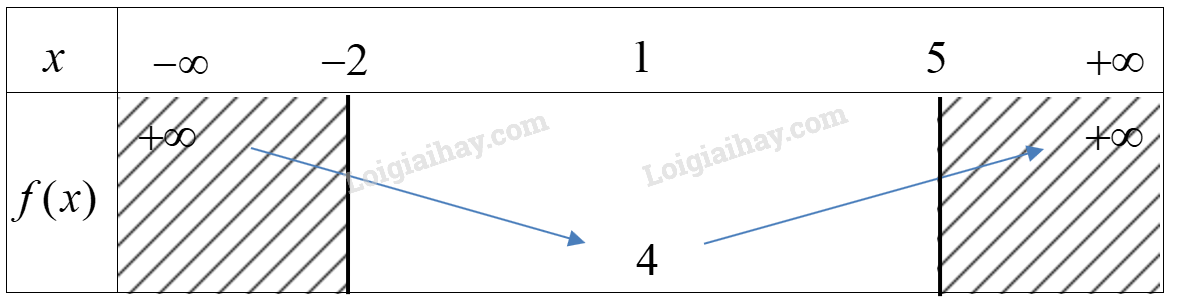
Ta có bảng biến thiên
Mà \(f( - 2) = 31,f(5) = 52,f(1) = 4\)
\( \Rightarrow \) Trên [-2;5] hàm số đạt GTLN bằng 52 tại \(x = 5\), đạt GTNN bằng 4 tại \(x = 1\).

Xem thêm : Đề thi, đề kiểm tra Toán lớp 10 - Cánh diều