Lấy ba ví dụ về cộng hai phân số có cùng mẫu số, rồi tính kết quả.
Muốn cộng hai phân số cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số.
Ví dụ:
$\frac{{10}}{{15}} + \frac{7}{{15}} = \frac{{17}}{{15}}$
$\frac{1}{9} + \frac{{22}}{9} = \frac{{23}}{9}$
$\frac{5}{{12}} + \frac{{13}}{{12}} = \frac{{18}}{{12}} = \frac{3}{2}$

Các bài tập cùng chuyên đề
Tính.
a) $\frac{1}{{10}} + \frac{3}{{10}}$
b) $\frac{5}{{12}} + \frac{1}{{12}}$
c) $\frac{3}{2} + \frac{1}{2}$
Viết các số hạng là số tự nhiên dưới dạng phân số rồi tính.
a) $\frac{1}{3} + 1$
b) $\frac{2}{5} + 2$
c) $7 + \frac{1}{2}$
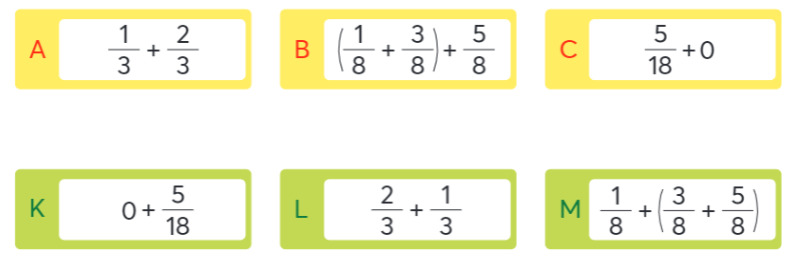
Các biểu thức nào có giá trị bằng nhau?
Nhận xét: Phép cộng các phân số có tính chất giao hoán và kết hợp. Một phân số cộng với 0 bằng chính phân số đó.
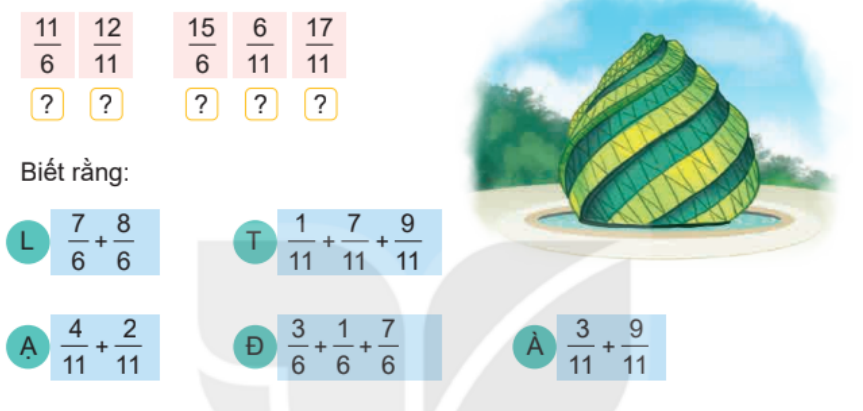
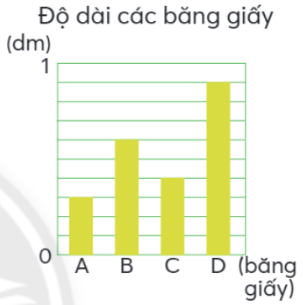
Quan sát biểu đồ bên.
a) Số?
b) Trong các phân số trên, phân số nào là tổng của hai trong ba phân số còn lại?
Dưới đây là một viên gạch bông gồm ba màu: vàng, xanh đậm và xanh nhạt.
a) Số?
$\frac{{....}}{{....}}$ viên gạch là màu vàng.
$\frac{{....}}{{....}}$ viên gạch là màu xanh đậm.
$\frac{{....}}{{....}}$ viên gạch là màu xanh nhạt.
b) Lớn hơn, bé hơn hay bằng?
Tổng hai phân số chỉ phần gạch màu vàng và màu xanh đậm ....... phân số chỉ phần gạch màu xanh nhạt.
Bạn Tí pha được một cốc nước chanh đầy. Tí uống một hơi hết $\frac{1}{3}$ cốc nước chanh. Thấy ngọt quá, Tí pha thêm nước cho đầy cốc rồi uống $\frac{2}{3}$ cốc. Thấy vẫn còn ngọt, Tí lại pha thêm nước cho đầy cốc rồi uống cạn.
Tính lượng nước bạn Tí đã pha thêm vào cốc nước chanh.
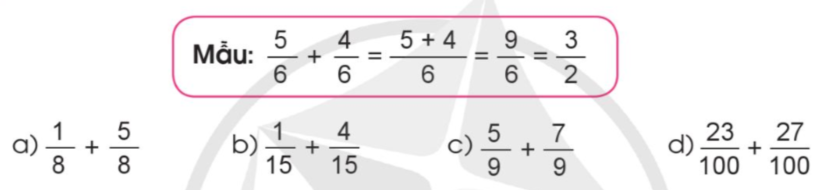
Tính (theo mẫu).
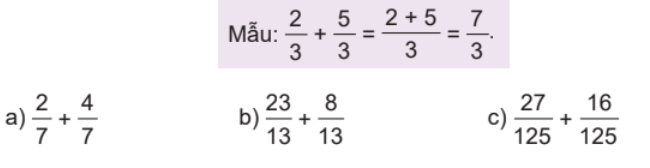
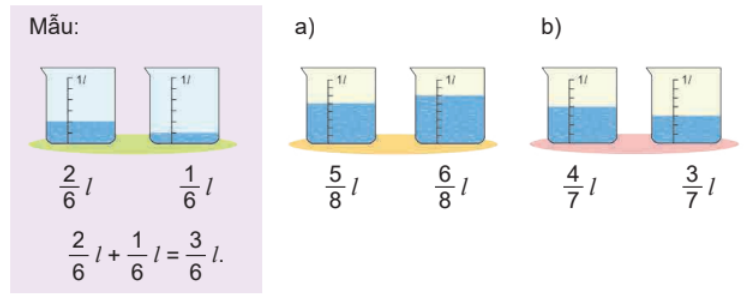
Viết phép tính thích hợp (theo mẫu).
Số?
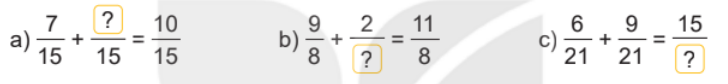
Mai dành hai ngày cuối tuần để đọc sách. Ngày thứ nhất, Mai đọc được $\frac{2}{7}$cuốn sách. Ngày thứ hai, Mai đọc thêm được $\frac{3}{7}$ cuốn sách. Hỏi cả hai ngày, Mai đọc được bao nhiêu phần của cuốn sách?
Đ, S?
Giải ô chữ dưới đây.
Cô Ba có một tấm vải. Cô dùng $\frac{7}{{15}}$ tấm vải để may quần, $\frac{4}{{15}}$ tấm vải để may áo và $\frac{2}{{15}}$ tấm vải để may túi. Hỏi cô Ba đã dùng tất cả bao nhiêu phần tấm vải?
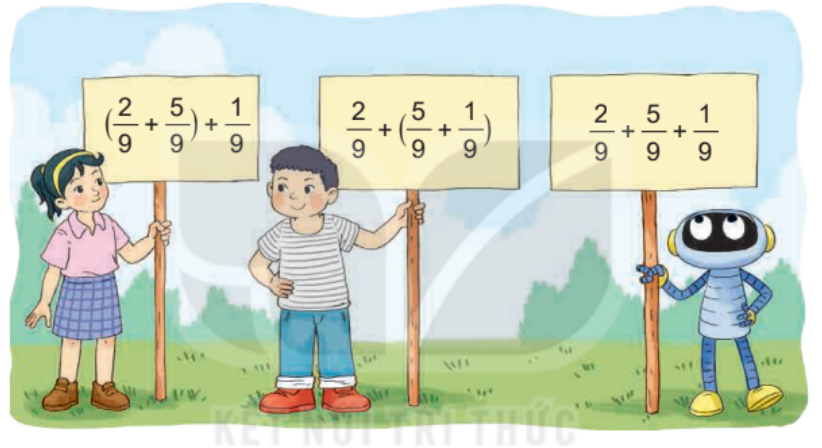
So sánh giá trị của các biểu thức dưới đây.
Tính bằng cách thuận tiện.
${\text{a) }}\frac{{16}}{{15}} + \frac{7}{{15}} + \frac{4}{{15}}$
${\text{b) }}\frac{5}{{17}} + \frac{7}{{17}} + \frac{{13}}{{17}}$
Tính bằng cách thuận tiện.
a) $\,\frac{{599}}{{1\,000}} + \frac{{377}}{{1\,000}} + \frac{1}{{1\,000}}\,\,$
b) $\frac{{15}}{4} + \frac{{15}}{{16}} + \frac{5}{{16}}$
Một xe ô tô chạy được $\frac{2}{7}$ quãng đường trong giờ đầu tiên. Giờ tiếp theo, ô tô chạy thêm được $\frac{3}{7}$ quãng đường. Hỏi sau hai giờ, ô tô chạy được mấy phần của quãng đường?
Tính bằng cách thuận tiện.
$\frac{4}{{27}} + \frac{5}{9} + \frac{{13}}{9} - 2$
Đố em!

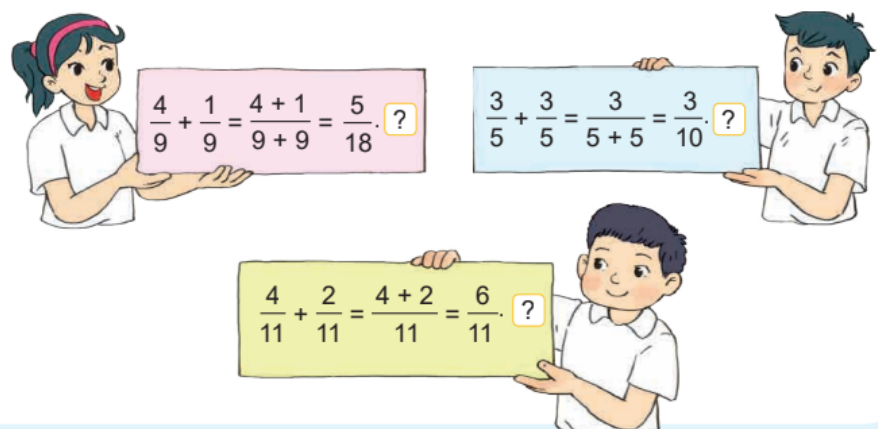
Em hãy giúp Nam và Việt thực hiện yêu cầu của Mai.
Tính:
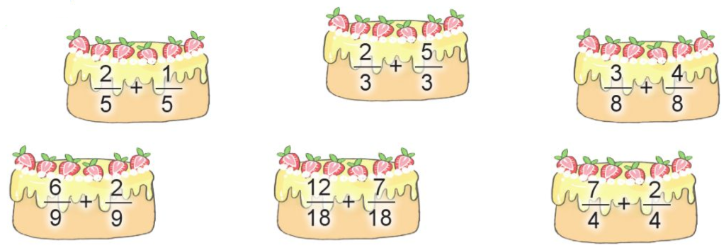
Tính rồi rút gọn (theo mẫu):
Chọn cách tính đúng:

Một đội công nhân sửa một đoạn đường, ngày thứ nhất sửa được $\frac{3}{7}$đoạn đường, ngày thứ hai sửa được $\frac{2}{7}$đoạn đường. Hỏi cả hai ngày đội công nhân sửa được bao nhiêu phần đoạn đường đó?
Một vòi nước chảy vào một bể. Giờ thứ nhất vòi nước chảy được $\frac{2}{5}$bể, giờ thứ hai vòi chảy tiếp được $\frac{1}{5}$ bể. Hỏi sau hai giờ vòi đó chảy được bao nhiêu phần của bể?
a) Tính rồi so sánh:

b) Lấy ví dụ tương tự câu a rồi đố bạn thực hiện.
a) Tính rồi so sánh:

b) Lấy ví dụ tương tự câu a rồi đố bạn thực hiện.
Tính:
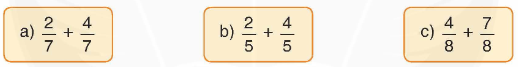
Tương tự số tự nhiên, phép cộng phân số có tính chất giao hoán.
Chẳng hạn $\frac{4}{5} + \frac{7}{9} = \frac{7}{9} + \frac{4}{5}$
Dựa vào kết quả ở bài 1, không tính, hãy cho biết kết quả của các phép tính sau:
$\frac{4}{7} + \frac{2}{7}$ ; $\frac{4}{5} + \frac{2}{5}$ và $\frac{7}{8} + \frac{4}{8}$
Hai vòi cùng chảy vào một bể nước. Vòi thứ nhất chảy được $\frac{3}{{10}}$ bể. Vòi thứ hai chảy được $\frac{1}{{10}}$bể. Hỏi cả hai vòi chảy được mấy phần bể nước?
Tính giá trị của biểu thức:









Danh sách bình luận