Bảng 3.11 trình bày dữ liệu về tốc độ của 100 xe ô tô lưu thông trên một đoạn đường cao tốc vào giờ cao điểm, được trích xuất từ camera của cơ quan cảnh sát giao thông. Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu (làm tròn kết quả đến hàng đơn vị). Nêu ý nghĩa của các kết quả tìm được.

- Khoảng biến thiên được xác định bằng giá trị đầu mút phải của nhóm cuối cùng trừ đầu mút trái của nhóm đầu tiên.
- Tìm tứ phân vị: \({Q_x} = L + \left( {\frac{{{n_x} - F}}{f}} \right) \times h\)
- Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
- Khoảng biến thiên là:
R = 110 – 60 = 50 km/h
- Tứ phân vị:
\(\frac{N}{4} = 25\) rơi vào nhóm [70; 80)
\({Q_1} = 70 + \frac{{25 - 10}}{{20}}.10 = 77,5\)
\(\frac{{3N}}{4} = 75\) rơi vào nhóm [90; 100)
\({Q_3} = 90 + \frac{{75 - 50}}{{35}}.10 \approx 97,1\)
- Khoảng tứ phân vị:
\({\Delta _Q} = {Q_3} - {Q_1} = 97,1 - 77,5 \approx 20\)km/h
- Kết quả của khoảng tứ phân vị cho thấy rằng tốc độ của phần lớn các xe ô tô khá đồng đều chỉ dao động trong một phạm vi không quá rộng. Điều này có thể cho thấy rằng, mặc dù có sự chênh lệch tổng thể về tốc độ (khoảng biến thiên lớn), phần lớn các xe di chuyển với tốc độ tương đối giống nhau.

Các bài tập cùng chuyên đề
Hãy giải bài toán trong tình huống mở đầu bằng cách sử dụng khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm.
Thống kê số thẻ vàng của mỗi câu lạc bộ trong giải ngoại hạng Anh mùa giải 2021-2022 cho kết quả như sau:

a) Hãy ghép nhóm dãy số liệu trên thành các nhóm có độ dài bằng nhau với nhóm đầu tiên là \(\left[ {40;50} \right)\).
b) Tính khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu gốc và mẫu số liệu ghép nhóm thu được ở câu a. Giá trị nào là giá trị chính xác? Giá trị nào là giá trị xấp xỉ?
Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:
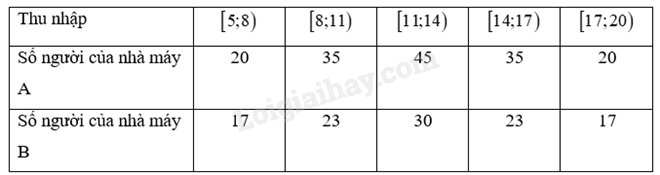
Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.
Bảng sau đây cho biết chiều cao của các học sinh lớp 12A và 12B.
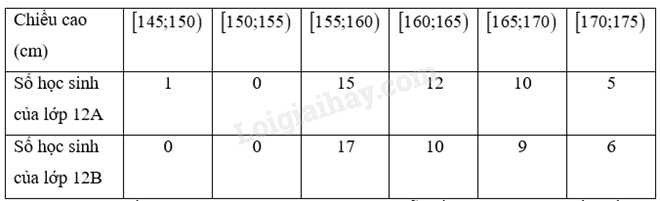 a) Tìm khoảng biến thiên, khoảng tứ phân vị cho các mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 12A, 12B.
a) Tìm khoảng biến thiên, khoảng tứ phân vị cho các mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 12A, 12B.
b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này ta nên dùng khoảng biến thiên hay khoảng tứ phân vị? Vì sao?
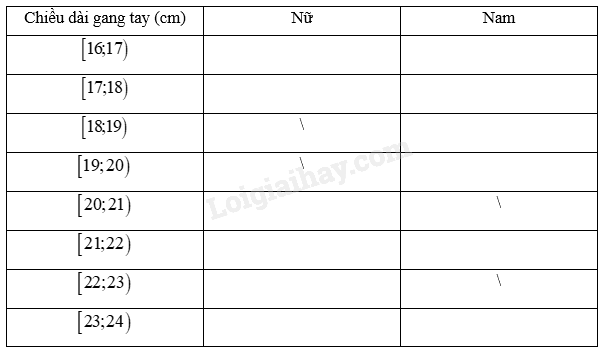
Lưu dữ liệu thu được vào bảng theo mẫu sau:
Bảng 8 biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày
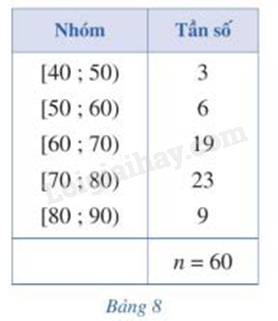
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
A. 50
B. 30
C. 6
D. 69,8
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:
A. 50
B. 40
C. 14,23
D. 70,87
Bảng 9 biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của 1 công ty (đơn vị: triệu đồng).
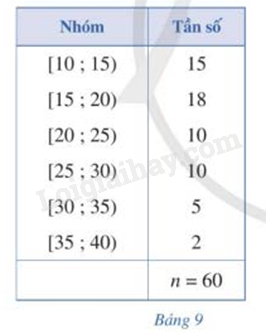
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.
Bảng 10 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố.
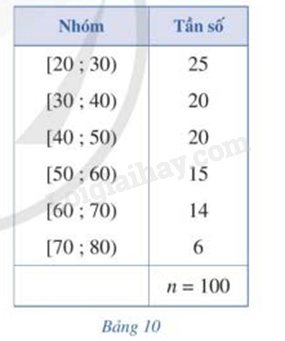
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.
Giả sử kết quả khảo sát hai khu vực A và B về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của từng mẫu số liệu ghép nhóm ứng với mỗi khu vực A và B.
b) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực nào có độ tuổi kết hôn đồng đều hơn?
a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm ở Ví dụ 4 sau khi đã loại bỏ các giá trị ngoại lệ. Em có nhận xét gì về khoảng biến thiên, khoảng tứ phân vị vừa tìm được và khoảng biến thiên, khoảng tứ phân vị ban đầu?
Hằng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian của 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan.

b) Hãy so sánh độ phân tán của nửa giữa hai mẫu số liệu chiều cao của các học sinh nữ lớp 12C và 12D ở Thực hành 1.

Bảng sau thống kê tổng lượng mưa (đơn vị: mm) đo được vào tháng 7 từ năm 2002 đến 2021 tại một trạm quan trắc đặt ở Cà Mau.

a) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu trên.
b) Hãy chia mẫu số liệu trên thành 4 nhóm với nhóm đầu tiên là [140; 240) và lập bảng tần số ghép nhóm.
c) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm và so sánh với kết quả tương ứng thu được ở câu a).
Kết quả đo chiều cao của 100 cây keo 3 năm tuổi tại một nông trường được cho ở bảng sau:

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
b) Trong 100 cây keo trên có 1 cây cao 8,4 m. Hỏi chiều cao của cây keo này có phải là giá trị ngoại lệ không?
Bảng thống kê sau cho biết dân số thế giới theo độ tuổi (đơn vị tính là triệu người) trong hai năm 2000 và 2020:
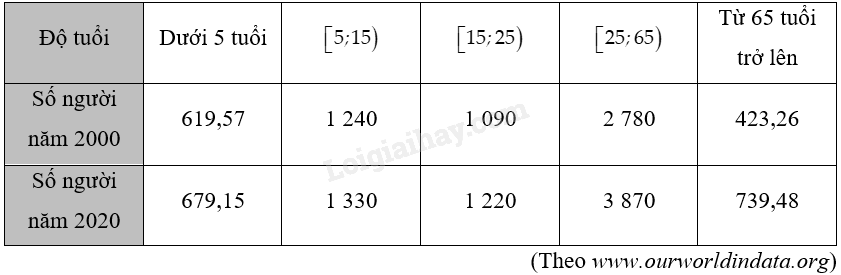
a) Chọn 75 là đại diện cho nhóm 65 tuổi trở lên. Hãy ước lượng tuổi trung bình của dân số thế giới trong hai năm 2000 và 2020.
b) Tìm khoảng tứ phân vị cho tuổi của dân số thế giới trong hai năm 2000 và 2020. Nêu nhận xét về sự thay đổi cấu trúc dân số theo độ tuổi.
Thống kê cân nặng của một số trẻ sơ sinh tại một bệnh viện cho kết quả như sau:

Tìm khoảng biến thiên và khoảng tứ phân vị cho mẫu số liệu ghép nhóm trên. Các giá trị này cho biết điều gì?
Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng 9.
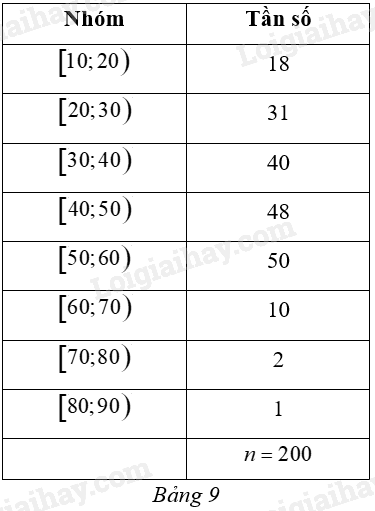
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = 90\) (tuổi).
b) Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{200}}{4} = 50\).
c) \({Q_3} = 52\frac{{17}}{{24}}\).
d) Khoảng tứ phân vị của mẫu số liệu lớn hơn 20.
Một cuộc khảo sát xác định số năm đã sử dụng của 160 chiếc ô tô. Kết quả điều tra được cho trong Bảng 10.
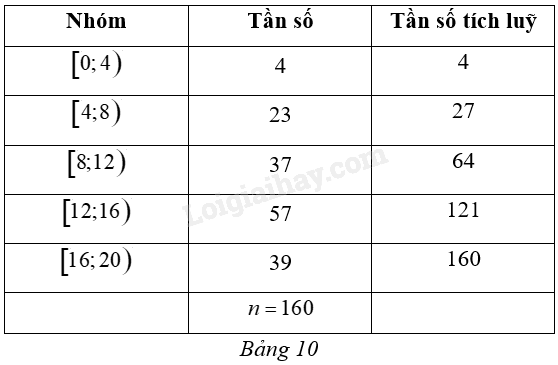
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó (làm tròn kết quả đến hàng phần mười).
Một thư viện thống kê số người đến đọc sách vào buổi tối trong 30 ngày của một tháng và kết quả được cho bởi Bảng 11.
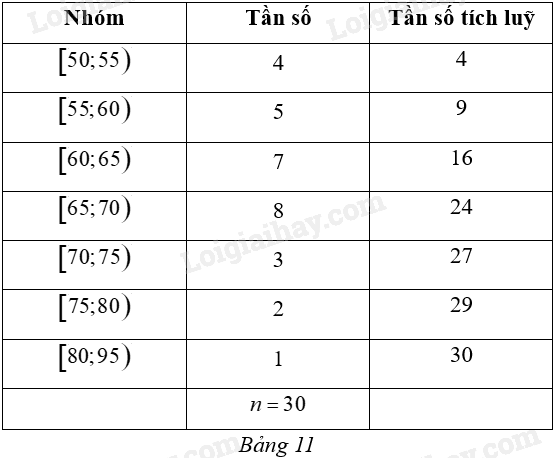
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó (làm tròn kết quả đến hàng đơn vị).
Thời gian đọc sách của một số người cao tuổi trong một tuần được ghi lại ở bảng sau:

Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến hàng phần trăm.)
Bảng sau cho biết thời gian hoàn thành cự li đi bộ 10000 m của một số học sinh:

Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến hàng phần mười.)
Một công ty du lịch ghi lại độ tuổi các du khách đặt một tour du lịch mạo hiểm ở bảng sau:

a) Hãy so sánh độ phân tán của độ tuổi du khách nam và du khách nữ theo khoảng biến thiên và khoảng tứ phân vị.
b) Biết rằng trong mẫu số liệu trên có một du khách nữ 49 tuổi. Hỏi độ tuổi của du khách nữ đó có là giá trị ngoại lệ khi so với độ tuổi của các du khách nữ không?
Bảng sau thống kê lương tháng của các nhân viên ở hai doanh nghiệp A và B.
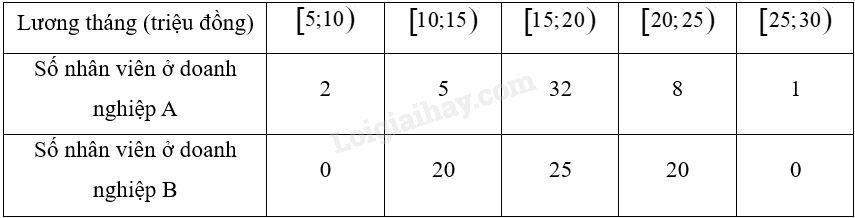
a) Hãy so sánh độ phân tán của mức lương ở hai doanh nghiệp theo khoảng biến thiên.
b) Hãy so sánh độ phân tán của mức lương ở hai doanh nghiệp theo khoảng tử phân vị.
c) Biết rằng có 1 nhân viên ở doanh nghiệp A có lương tháng là 27 triệu đồng. Lương tháng của nhân viên này có phải là một giá trị ngoại lệ không? Tại sao?
Kết quả khảo sát cân nặng của 80 con tôm càng xanh 5 tháng tuổi ở một khu nuôi tôm được biểu diễn ở biểu đồ tần số dưới đây.
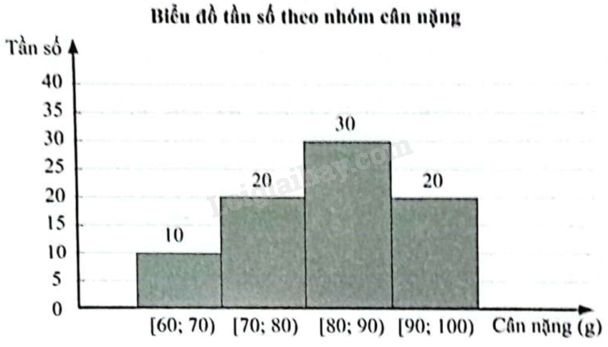
a) Hãy lập bảng tần số ghép nhóm cho mẫu số liệu trên.
b) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
Dưới đây là kết quả điều tra thời gian hoàn thành bài tập ở nhà môn Toán của 30 học sinh lớp 9:
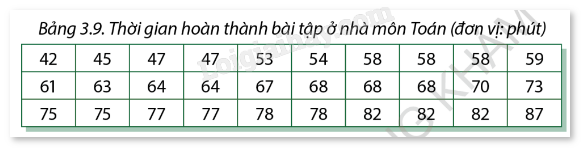
a) Tìm trung bình, các tứ phân vị và khoảng tứ phân vị của mẫu số liệu đã cho.
b) Lập mẫu số liệu ghép nhóm với các nhóm ghép có độ dài bằng 10 và nhóm đầu tiên là [40;50).
c) Tìm trung bình, khoảng biến thiên, các tứ phân vị và khoảng tứ phân vị của mẫu số liệu ghép nhóm lập ở câu b.
d) So sánh các kết quả tìm được ở câu a và c. Giải thích vì sao có sự khác biệt.
Thời gian trung bình hằng ngày mà một số nhân viên đi từ nhà đến công ty được thống kê trong Bảng 3.10. Tìm khoảng biến thiên và khoảng tứ phân vị của thời gian di chuyển đến công ty của các nhân viên (làm tròn kể quả đến hàng phần mười).

Thống kê số ngày trong tháng Sáu năm 2021 và năm 2022 theo nhiệt độ cao nhất trong ngày tại Hà Nội, người ta thu được bảng sau:

Hỏi tháng Sáu năm nào ở Hà Nội nhiệt độ cao nhất trong ngày biến đổi nhiều hơn?
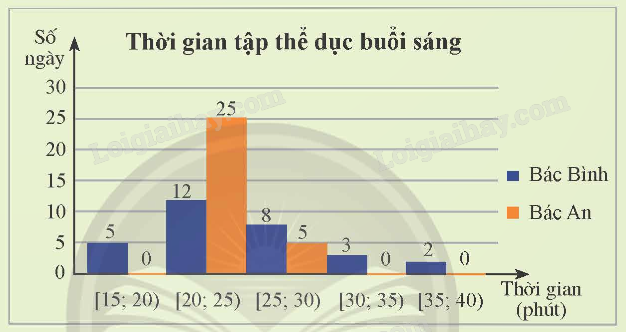
Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An.
Ai là người có thời gian tập đều hơn?
Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng.

Xét tính đúng, sai của các mệnh đề sau:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: $R = 90$ (tuổi).
b) Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\dfrac{n}{4} = \dfrac{200}{4} = 50$.
c) $Q_{3} = \dfrac{17}{4}$.
d) Khoảng tứ phân vị của mẫu số liệu lớn hơn 20.







Danh sách bình luận